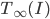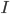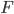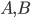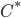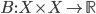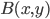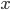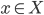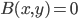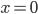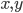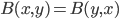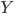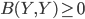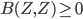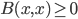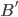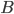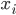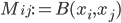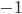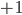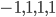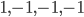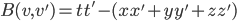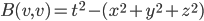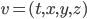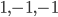Category Archives: Mathematics

Strongly Symmetric Spectral Convex Sets are Jordan Algebra State Spaces

Posted on by

The title of this post is also the title of my most recent paper on the arXiv, from 2019, with Joachim Hilgert of the University of Paderborn. The published version is titled Spectral Properties of Convex Bodies, Journal of Lie Theory 30 (2020) 315-355.

Here's a preprint version of the J Lie Theory article:

BarnumHilgertSpectralPropertiesOfConvexBodiesPreprintVersion2Download

Compared to the arXiv version, the J Lie Theory version (and the above-linked preprint) has less detail about the background results by other authors (mainly Jiri Dadok's theory of polar representations of compact Lie groups, and the Madden-Robertson theory of regular convex bodies) which we use, and a bit more detail in the proof of our main result. It also has a more extensive discussion of infinite-dimensional Jordan algebraic systems, in the context of discussion of ways in which the Jordan algebraic systems can be narrowed down to the complex quantum ones. I like the title of the arXiv version better, since it states the main result of the paper, but Joachim was scheduled to give a talk at the celebration of Jimmie Lawson's 75th birthday in 2018, while we were writing up the main result, so he gave a talk on our work titled Spectral Properties…, and we decided to publish the paper in the proceedings, which are a special issue of J Lie Theory, so it ended up with the same title as the talk.

Here are slides from a talk on the result I gave to an audience of mathematicians and mathematical physicists:

MadridOperatorAlgebras2019

MadridOperatorAlgebras2019Download

Although the paper's main theorem is a result in pure mathematics, and, I think, interesting even purely from that point of view, it is also a result in the generalized probabilistic theories (GPT) framework for formulating physical theories from a very general point of view, which describes physical systems in terms of the probabilities of the various results of all possible ways of observing (we often say "measuring") those systems. The state in which a system has been prepared (whether by an experimenter or by some natural process) is taken to be defined by specifying these probabilities of measurement-results, and it is then very natural to take the set of all possible states in which a system can be prepared to be a compact convex set. Such sets are usually taken to live in some real affine space, for instance the three-dimensional one of familiar Euclidean geometry, which may be taken to host the qubit, whose state space is a solid ball, sometimes called the Bloch ball. In this framework, measurement outcomes are associated with affine functionals on the set taking real values---in fact, values between 0 and 1 --- probabilities, and measurements are associated with lists of such functionals, which add up to the unit functional---the constant functional taking the value 1 on all states of the system. (This ensures that whatever state of the system is prepared, the probabilities of outcomes of a measurement add up to 1.) This allows an extremely wide variety of convex sets as state spaces, most of which are neither the state spaces of quantum systems nor classical systems. An important part of the research program of those of us who spend some of our time working in the GPT framework is to characterize the state spaces of quantum systems by giving mathematically natural axioms, or axioms concerning the physical properties exhibited by, or the information-processing protocols we can implement using, such systems, such that all systems having these properties are quantum systems. To take just a few examples of the type of properties we might ask about: can we clone states of such systems? Do we have what Schroedinger called "steering" using entangled states of a pair of such systems? Can we define a notion of entropy in a way similar to the way we define the von Neumann entropy of a quantum system, and if so, are there thermodynamic protocols or processes similar to those possible with quantum systems, in which the entropy plays a similar role? Are there analogues of the spectral theorem for quantum states (density matrices), of the projection postulate of quantum theory, of the plethora of invertible transformations of the state space that are described, in the quantum case, by unitary operators? We often limit ourselves (as Joachim and I did in our paper) to finite-dimensional GPT systems to make the mathematics easier while still allowing most of the relevant conceptual points to become clear.

This paper with Joachim builds on work by me, Markus Mueller and Cozmin Ududec, who showed that three principles characterize irreducible finite-dimensional Jordan-algebraic systems (plus finite-dimensional classical state spaces). Since these systems were shown (by Jordan, von Neumann, and Wigner in the 1930s, shortly after Jordan defined the algebras named after him) to be just the finite-dimensional quantum systems over the real, complex, and quaternionic numbers, plus systems whose state space is a ball (of any finite dimension), plus three-dimensional quantum theory over the octonions (associated with the so-called exceptional Jordan algebra), this already gets us very close to a characterization of the usual complex quantum state space (of density matrices) and the associated measurement theory described by positive operators. The principles are (1) A generalized spectral decomposition: every state is a convex combination of perfectly distinguishable pure states, (2) Strong Symmetry: every set of perfectly distinguishable pure states may be taken to any other such set (of the same size) by a symmetry of the state space, and (3) that there is no irreducible three (or more) path interference. Joachim and I characterized the same class of systems using only (1) and (2). In order for you to understand these properties, I need to explain some terms used in them: pure states are defined as states that cannot be viewed as convex combinations of any other states---that is, there is no "noise" involved in their preparation---they are sometimes called "states of maximal information". The states in a given list of states are "perfectly distinguishable" from each other if, when we are guaranteed that the state of a system is one of those in the list, there is a single measurement that can tell us which state it is. The measurement that does the distinguishing may, of course, depend on which list it is. Indeed one can take it as a definition of classical system, at least in this finite-dimensional context, that there is a single measurement that is capable of distinguishing the states in any list of distinct pure states of the system.

If one wants to narrow things down further from the Jordan-algebraic systems to the complex quantum systems, there are known principles that will do it: for instance, energy observability (from the Barnum, Mueller, Ududec paper linked above, although it should be noted that it's closely related to concepts of Alfsen and Shultz ("dynamical correspondence") and of Connes ("orientation")): that the generators of continuous symmetries of the state space are also observables, and are conserved by the dynamics that they generate, a requirement very reminiscent of Noether's theorem on conserved generators of symmetries. Mathematically speaking, we formulate this as a requirement that the Lie algebra of the symmetry group of the state space embeds, injectively and linearly, into the space of observables (which we take to be the ambient real vector space spanned by the measurement outcomes) of the system, in such a way that the embedded image of a Lie algebra generator is conserved by the dynamics it generates. In the quantum case, this is just the fact that the Lie algebra su(n) of an n-dimensional quantum system's symmetry group is the real vector space of anti-Hermitian matrices, which embeds linearly (over the reals) and injectively into the Hermitian matrices (indeed, bijectively onto the traceless Hermitian matrices), which are of course the observables of a finite-dimensional quantum system. This embedding is so familiar to physicists that they usually just consider the generators of the symmetry group to be Hermitian matrices ("Hamiltonians"), and map them back to the antiHermitian generators by considering multiplication by i (that's the square root of -1) as part of the "generation" of unitary evolution. This is discussed in the arXiv version, but the Journal of Lie Theory version discusses it more extensively, and along the way indicates some results on infinite-dimensional Jordan algebraic systems since Alfsen and Shultz, and Connes, worked in frameworks allowing some infinite-dimensional systems. See also John Baez' excellent recent paper, Getting to the Bottom of Noether's Theorem. One can also narrow things down to complex quantum systems by requiring that systems compose in a "tomographically local" way, which means that there is a notion of composite system, made up of two distinct systems, such that all states of the composite system, even the entangled ones (a notion which makes sense in this general probabilistic context, not only in quantum theory), are determined by the probabilities they give to pairs of local meausurement outcomes (i.e. the way in which they correlate (or fail to correlate) these outcomes).

Martin Idel: the fixed-point sets of positive trace-preserving maps on quantum systems are Jordan algebras!

Posted on by

Kasia Macieszczak is visiting the ITP at Leibniz Universität Hannover (where I arrived last month, and where I'll be based for the next 7 months or so), and gave a talk on metastable manifolds of states in open quantum systems.  She told me about a remarkable result in the Master's thesis of Martin Idel at Munich: the fixed point set of any trace-preserving, positive (not necessarily completely positive) map on the space of Hermitian operators of a finite-dimensional quantum system, is a Euclidean Jordan algebra.  It's not necessarily a Jordan subalgebra of the usual Jordan algebra associated with the quantum system (whose Jordan product is the antisymmetrized matrix multiplication, ).  We use the usual characterization of the projector onto the fixed-point space of a linear map :  .  The maximum-rank fixed point is (where is the identity matrix), which we'll call , and the Jordan product on the fixed-point space is the original one "twisted" to have as its unit:  for fixed-points, this Jordan product, which I'll denote by , is:

which we could also write in terms of the original Jordan product as , where is the map defined by .

Idel's result, Theorem 6.1 in his thesis, is stated in terms of the map on all complex matrices, not just the  Hermitian ones; the fixed-point space is then the complexification of the Euclidean Jordan algebra.  In the case of completely positive maps, this complexification is "roughly a algebra" according to Idel.  (I suspect, but don't recall offhand, that it is a direct sum of full matrix algebras, i.e. isomorphic to a quantum system composed of several "superselection sectors" (the full matrix algebras in the sum), but as in the Euclidean case, not necessarily a -subalgebra of the ambient matrix algebra.)

I find this a remarkable result because I'm interested in places where Euclidean Jordan algebras appear in nature, or in mathematics.  One reason for this is that the finite-dimensional ones are in one-to-one correspondence with homogeneous, self-dual cones; perhaps I'll discuss this beautiful fact another time.  Alex Wilce, Phillip Gaebeler and I related the property of homogeneity to "steering" (which Schrödinger considered a fundamental weirdness of the newly developed quantum theory) in this paper.  I don't think I've blogged about this before, but Matthew Graydon, Alex Wilce, and I have developed ways of constructing composite systems of the general probabilistic systems based on reversible Jordan algebras, along with some results that I interpret as no-go theorems for such composites when one of the factors is not universally reversible.  The composites are still based on Jordan algebras, but are necessarily (if we wish them to still be Jordan-algebraic) not locally tomographic unless both systems are quantum.  Perhaps I'll post more on this later, too.  For now I just wanted to describe this cool result of Martin Idel's that I'm happy to have learned about today from Kasia.

ITFP, Perimeter: selective guide to talks. #1: Brukner on quantum theory with indefinite causal order

Posted on by

Excellent conference the week before last at Perimeter Institute: Information Theoretic Foundations for Physics.  The talks are online; herewith a selection of some of my favorites, heavily biased towards ideas new and particularly interesting to me (so some excellent ones that might be of more interest to you may be left off the list!).  Some of what would have been possibly of most interest and most novel to me happened on Weds., when the topic was spacetime physics and information, and I had to skip the day to work on a grant proposal.  I'll have to watch those online sometime.  This was going to be one post with thumbnail sketches/reviews of each talk, but as usual I can't help running on, so it may be one post per talk.

All talks available here, so you can pick and choose. Here's #1 (order is roughly temporal, not any kind of ranking...):

Caslav Brukner kicked off with some interesting work on physical theories in with indefinite causal structure.  Normally in formulating theories in an "operational" setting (in which we care primarily about the probabilities of physical processes that occur as part of a complete compatible set of possible processes) we assume a definite causal (partial) ordering, so that one process may happen "before" or "after" another, or "neither before nor after".  The formulation is "operational" in that an experimenter or other agent may decide upon, or at least influence, which set of processes, out of possible compatible sets, the actual process will be drawn, and then nature decides (but with certain probabilities for each possible process, that form part of our theory), which one actually happens.  So for instance, the experimenter decides to perform a Stern-Gerlach experiment with a particular orientation X of the magnets; then the possible processes are, roughly, "the atom was deflected in the X direction by an angle theta," for various angles theta.  Choose a different orientation, Y, for your apparatus, you choose a different set of possible compatible processes.  ("The atom was deflected in the Y direction by an angle theta.")  Then we assume that if one set of compatible processes happens after another, an agent's choice of which complete set of processes is realized later, can't influence the probabilities of processes occuring in an earlier set.  "No signalling from the future", I like to call this; in formalized operational theories it is sometimes called the "Pavia causality axiom".   Signaling from the past to the future is fine, of course.  If two complete  sets of processes are incomparable with respect to causal order ("spacelike-separated"), the no-signalling constraint operates both ways:  neither Alice's choice of which compatible set is realized, nor Bob's, can influence the probabilities of processes occuring at the other agent's site.   (If it could, that would allow nearly-instantaneous signaling between spatially separated sites---a highly implausible phenomenon only possible in preposterous theories such as the Bohmian version of quantum theory with "quantum disequilibrium", and Newtonian gravity. ) Anyway, Brukner looks at theories that are close to quantum, but in which this assumption doesn't necessarily apply: the probabilities exhibit "indeterminate causal structure".  Since the theories are close to quantum, they can be interpreted as allowing "superpositions of different causal structures", which is just the sort of thing you might think you'd run into in, say, theories combining features of quantum physics with features of general relativistic spacetime physics.  As Caslav points out, since in general relativity the causal structure is influenced by the distribution of mass and energy, you might hope to realize such indefinite causal structure by creating a quantum superposition of states in which a mass is in one place, versus being in another.  (There are people who think that at some point---some combinations of spatial scales (separation of the areas in which the mass is located) and mass scales (amount of mass to be separated in "coherent" superposition)) the possibility of such superpositions breaks down.  Experimentalists at Vienna (where Caslav---a theorist, but one who likes to work with experimenters to suggest experiments---is on the faculty) have created what are probably the most significant such superpositions.)

Situations with a superposition of causal orders seem to be exhibit some computational advantages over standard causally-ordered quantum computation, like being able to tell in fewer queries (one?) whether a pair of unitaries commutes or anticommutes.  Not sure whose result that was (Giulio Chiribella and others?), but Caslav presents some more recent results on query complexity in this model, extending the initial results.  I am generally wary about results on computation in theories with causal anomalies.  The stuff on query complexity with closed timelike curves, e.g. by Dave Bacon and by  Scott Aaronson and John Watrous has seemed uncompelling---not the correctness of the mathematical results, but rather the physical relevance of the definition of computation---to me for reasons similar to those given by Bennett, Leung, Smith and Smolin.  But I tend to suspect that Caslav and the others who have done these query results, use a more physically compelling framework because they are well versed in the convex operational or "general probabilistic theories" framework which aims to make the probabilistic behavior of processes consistent under convex combination ("mixture", i.e. roughly speaking letting somebody flip coins to decide which input to present your device with).  Inconsistency with respect to such mixing is part of the Bennett/Leung/Smolin/Smith objection to the CTC complexity classes as originally defined.

[Update:  This article at Physics.org quotes an interview with Scott Aaronson responding to the Bennett et. al. objections.  Reasonably enough, he doesn't think the question of what a physically relevant definition of CTC computing is has been settled.  When I try to think about this issue sometimes I wonder if the thorny philosophical question of whether we court inconsistency by trying to combine intervention ("free choice of inputs") in a physical theory is rearing its head.  As often with posts here, I'm reminding myself to revisit the issue at some point... and think harder.]

A thought on resistance to Bayesian statistics

Posted on by

I'm not a statistician, and as a quantum theorist of a relatively abstract sort, I've done little actual data analysis.  But because of my abstract interests, the nature of probability and its use in making inferences from data are of great interest.  I have some relatively ill-informed thoughts on why the "classical statistics" community seems to have been quite resistant to "Bayesian statistics", at least for a while, that may be of interest, or at least worth logging for my own reference. Take this post in the original (?) spirit of the term "web log", rather than as a polished piece of the sort many blogs, functioning more in the spirit of online magazines, seem to aim at nowadays.

The main idea is this.  Suppose doing Bayesian statistics is thought of as actually adopting a prior which specifies, say, one's initial estimate of the probabilities of several hypotheses, and then, on the basis of the data, computing the posterior probability of the hypotheses.  In other words, what is usually called "Bayesian inference". That may be a poor way of presenting the results of an experiment, although it is a good way for individuals to reason about how the results of the experiment should affect their beliefs and decisions.  The problem is that different users of the experimental results, e.g. different readers of a published study, may have different priors.  What one would like is rather to present these users with a statistic, that is, some function of the data, much more succinct than simply publishing the data themselves, but just as useful, or almost as useful, in making the transition from prior probabilities to posterior probabilities, that is, of updating one's beliefs about the hypotheses of interest, to take into account the new data. Of course, for a compressed version of the data (a statistic) to be useful, it is probably necessary that the users share certain basic assumptions about the nature of the experiment.  These assumptions might involve the probabilities of various experimental outcomes, or sets of data, if various hypotheses are true (or if a parameter takes various values), i.e., the likelihood function;  they might also involve a restriction on the class of priors for which the statistic is likely to be useful.  These should be spelled out, and, if it is not obvious, how the statistic can be used in computing posterior probabilities should be spelled out as well.

It seems to me likely that many classical or "frequentist" statistics may be used in such a way; but, quite possibly, classical language, like saying that statistical inference leads to "acceptance" or "rejection" of hypotheses, tends to obscure this more desirable use of the statistic as a potential input to the computation of posterior probabilities.  In fact, I think people tend to have a natural tendency to want some notion of what the posterior probability of a hypothesis is; this is one source of the erroneous tendency, still sometimes found among the public, to confuse confidence levels with probabilities.  Sometimes an advocacy of classical statistical tests may go with an ideological resistance to the computation of posterior probabilities, but I suppose not always.  It also seems likely that in many cases, publishing actual Bayesian computations may be a good alternative to classical procedures, particularly if one is able to summarize in a formula what the data imply about posterior probabilities, for a broad enough range of priors that many or most users would find their prior beliefs adequately approximated by them.  But in any case, I think it is essential, in order to properly understand the meaning of reports of classical statistical tests, to understand how they can be used as inputs to Bayesian inference.  There may be other issues as well, e.g. that in some cases classical tests may make suboptimal use of the information available in the data.  In other words, they may not provide a sufficient statistic: a function of the data that contains all the information available in the data, about some random variable of interest (say, whether a particular hypothesis is true or not). Of course whether or not a statistic is sufficient will depend on how one models the situation.

Most of this is old hat, but it is worth keeping in mind, especially as a Bayesian trying to understand what is going on when "frequentist" statisticians get defensive about general Bayesian critiques of their methods.

No new enlightenment: A critique of "quantum reason"

Posted on by

I have a lot of respect for Scientific American contributing physics editor George Musser's willingness to solicit and publish articles on some fairly speculative and, especially, foundational, topics whether in string theory, cosmology, the foundations of quantum theory, quantum gravity, or quantum information.  I've enjoyed and learned from these articles even when I haven't agreed with them.  (OK, I haven't enjoyed all of them of course... a few have gotten under my skin.)  I've met George myself, at the most recent FQXi conference; he's a great guy and was very interested in hearing, both from me and from others, about cutting-edge research.  I also have a lot of respect for his willingness to dive in to a fairly speculative area and write an article himself, as he has done with "A New Enlightenment" in the November 2012 Scientific American (previewed here).  So although I'm about to critique some of the content of that article fairly strongly, I hope it won't be taken as mean-spirited.  The issues raised are very interesting, and I think we can learn a lot by thinking about them; I certainly have.

The article covers a fairly wide range of topics, and for now I'm just going to cover the main points that I, so far, feel compelled to make about the article.  I may address further points later; in any case, I'll probably do some more detailed posts, maybe including formal proofs, on some of these issues.

The basic organizing theme of the article is that quantum processes, or quantum ideas, can be applied to situations which social scientists usually model as involving the interactions of "rational agents"...or perhaps, as they sometimes observe, agents that are somewhat rational and somewhat irrational.  The claim, or hope, seems to be that in some cases we can either get better results by substituting quantum processes (for instance, "quantum games", or "quantum voting rules") for classical ones, or perhaps better explain behavior that seems irrational.  In the latter case, in this article, quantum theory seems to be being used more as a metaphor for human behavior than as a model of a physical process underlying it.  It isn't clear to me whether we're supposed to view this as an explanation of irrationality, or in some cases as the introduction of a "better", quantum, notion of rationality.  However, the main point of this post is to address specifics, so here are four main points; the last one is not quantum, just a point of classical political science.

 

(1) Quantum games.  There are many points to make on this topic.  Probably most important is this one: quantum theory does not resolve the Prisoner's Dilemma.  Under the definitions I've seen of "quantum version of a classical game", the quantum version is also a classical game, just a different one.  Typically the strategy space is much bigger.  Somewhere in the strategy space, typically as a basis for a complex vector space ("quantum state space") of strategies, or as a commuting ("classical") subset of the possible set of "quantum actions" (often unitary transformations, say, that the players can apply to physical systems that are part of the game-playing apparatus), one can set things up so one can compare the expected payoff of the solution, under various solution concepts such as Nash equilibrium, for the classical game and its "quantum version", and it may be that the quantum version has a better result for all players, using the same solution concept.  This was so for Eisert, Lewenstein, and Wilkens' (ELW for short) quantum version of Prisoner's Dilemma.  But this does not mean (nor, in their article, did ELW claim it did) that quantum theory "solves the Prisoner's Dilemma", although I suspect when they set out on their research, they might have had hope that it could.  It doesn't because the prisoners can't transform their situation into quantum prisoners dilemma; to play that game, whether by quantum or classical means, would require the jailer to do something differently.  ELW's quantum prisoner's dilemma involves starting with an entangled state of two qubits.  The state space consists of the unit Euclidean norm sphere in a 4-dimensional complex vector space (equipped with Euclidean inner product); it has a distinguished orthonormal basis which is a product of two local "classical bases", each of which is labeled by the two actions available to the relevant player in the classical game.  However the quantum game consists of each player choosing a unitary operator to perform on their local state.  Payoff is determined---and here is where the jailer must be complicit---by performing a certain two-qubit unitary---one which does not factor as a product of local unitaries---and then measuring in the "classical product basis", with payoffs given by the classical payoff corresponding to the label of the basis vector corresponding to the result.  Now, Musser does say that "Quantum physics does not erase the original paradoxes or provide a practical system for decision making unless public officials are willing to let people carry entangled particles into the voting booth or the police interrogation room."  But the situation is worse than that.  Even if prisoners could smuggle in the entangled particles (and in some realizations of prisoners' dilemma in settings other than systems of detention, the players will have a fairly easy time supplying themselves with such entangled pairs, if quantum technology is feasible at all), they won't help unless the rest of the world, implementing the game, implements the desired game, i.e. unless the mechanism producing the payoffs doesn't just measure in a product basis, but implements the desired game by measuring in an entangled basis.  Even more importantly, in many real-world games, the variables being measured are already highly decohered; to ensure that they are quantum coherent the whole situation has to be rejiggered.  So even if you didn't need the jailer to make an entangled measurement---if the measurement was just his independently asking each one of you some question---if all you needed was to entangle your answers---you'd have to either entangle your entire selves, or covertly measure your particle and then repeat the answer to the jailer.  But in the latter case, you're not playing the game where the payoff is necessarily based on the measurement result: you could decide to say something different from the measurement result.  And that would have to be included in the strategy set.

There are still potential applications:  if we are explicitly designing games as mechanisms for implementing some social decision procedure, then we could decide to implement a quantum version (according to some particular "quantization scheme") of a classical game.  Of course, as I've pointed out, and as ELW do in their paper, that's just another classical game.  But as ELW note, it is possible---in a setting where quantum operations (quantum computer "flops") aren't too much more expensive than their classical counterparts---that playing the game by quantum means might use less resources than playing it by simulating it classically.  In a mechanism design problem that is supposed to scale to a large number of players, it even seems possible that the classical implementation could scale so badly with the number of players as to become infeasible, while the quantum one could remain efficient.  For this reason, mechanism design for preference revelation as part of a public goods provision scheme, for instance, might be a good place to look for applications of quantum prisoners-dilemma like games.  (I would not be surprised if this has been investigated already.)

Another possible place where quantum implementations might have an advantage is in situations where one does not fully trust the referee who is implementing the mechanism.  It is possible that quantum theory might enable the referee to provide better assurances to the players that he/she has actually implemented the stated game.  In the usual formulation of game theory, the players know the game, and this is not an issue.  But it is not necessarily irrelevant in real-world mechanism design, even if it might not fit strictly into some definitions of game theory.  I don't have a strong intuition one way or the other as to whether or not this actually works but I guess it's been looked into.

(2) "Quantum democracy".  The part of the quote, in the previous item, about taking entangled particles into the voting booth, alludes to this topic.  Gavriel Segre has a 2008 arxiv preprint entitled "Quantum democracy is possible" in which he seems to be suggesting that quantum theory can help us the difficulties that Arrow's Theorem supposedly shows exist with democracy.  I will go into this in much more detail in another post.  But briefly, if we consider a finite set A of "alternatives", like candidates to fill a single position, or mutually exclusive policies to be implemented, and a finite set I of "individuals" who will "vote" on them by listing them in the order they prefer them, a "social choice rule" or "voting rule" is a function that, for every "preference profile", i.e. every possible indexed set of preference orderings (indexed by the set of individuals), returns a preference ordering, called the "social preference ordering", over the alternatives.  The idea is that then whatever subset of alternatives is feasible, society should choose the one mostly highly ranked by the social preference ordering,  from among those alternatives that are feasible.  Arrow showed that if we impose the seemingly reasonable requirements that if everyone prefers x to y, society should prefer x to y ("unanimity") and that whether or not society prefers x to y should be affected only by the information of which individuals prefer x to y, and not by othe aspects of individuals' preference orderings ("independence of irrelevant alternatives", "IIA"), the only possible voting rules are the ones such that, for some individual i called the "dictator" for the rule, the rule is that that individual's preferences are the social preferences.  If you define a democracy as a voting rule that satisfies the requirements of unanimity and IIA and that is not dictatorial, then "democracy is impossible".  Of course this is an unacceptably thin concept of individual and of democracy.  But anyway, there's the theorem; it definitely tells you something about the limitations of voting schemes, or, in a slighlty different interpretation, of the impossibility of forming a reasonable idea of what is a good social choice, if all that we can take into account in making the choice is a potentially arbitrary set of individuals' orderings over the possible alternatives.

Arrow's theorem tends to have two closely related interpretations:  as a mechanism for combining actual individual preferences to obtain social preferences that depend in desirable ways on individual ones, or as a mechanism for combining formal preference orderings stated by individuals, into a social preference ordering.  Again this is supposed to have desirable properties, and those properties are usually motivated by the supposition that the stated formal preference orderings are the individuals' actual preferences, although I suppose in a voting situation one might come up with other motivations.  But even if those are the motivations, in the voting interpretation, the stated orderings are somewhat like strategies in a game, and need not coincide with agents' actual preference orderings if there are strategic advantages to be had by letting these two diverge.

What could a quantum mitigation of the issues raised by Arrow's theorem---on either interpretation---mean?  We must be modifying some concept in the theorem... that of an individual's preference ordering, or voting strategy, or that of alternative, or---although this seems less promising---that of individual---and arguing that somehow that gets us around the problems posed by the theorem.  None of this seems very promising, for reasons I'll get around to in my next post.  The main point is that if the idea is similar to the --- as we've seen, dubious --- idea that superposing strategies can help in quantum games, it doesn't seem to help with interpretations where the individual preference ordering is their actual preference ordering.  How are we to superpose those?  Superposing alternatives seems like it could have applications in a many-worlds type interpretation of quantum theory, where all alternatives are superpositions to begin with, but as far as I can see, Segre's formalism is not about that.  It actually seems to be more about superpositions of individuals, but one of the big motivational problems with Segre's paper is that what he "quantizes" is not the desired Arrow properties of unanimity, independence of irrelevant alternatives, and nondictatoriality, but something else that can be used as an interesting intermediate step in proving Arrow's theorem.  However, there are bigger problems than motivation:  Segre's main theorem, his IV.4, is very weak, and actually does not differentiate between quantum and classical situations.  As I discuss in more detail below, it looks like for the quantum logics of most interest for standard quantum theory, namely the projection lattices of of von Neumann algebras, the dividing line between ones having what Segre would call a "democracy", a certain generalization of a voting rule satisfying Arrow's criteria, and ones that don't (i.e. that have an "Arrow-like theorem") is not commutativity versus noncommutativity of the algebra (ie., classicality versus quantumness), but just infinite-dimensionality versus finite-dimensionality, which was already understood for the classical case.  So quantum adds nothing.  In a later post, I will go through (or post a .pdf document) all the formalities, but here are the basics.

Arrow's Theorem can be proved by defining a set S of individuals to be decisive if for every pair x,y of alternatives, whenever everyone in S prefers x to y, and everyone not in x prefers y to x, society prefers x to y.  Then one shows that the set of decisive sets is an ultrafilter on the set of individuals.  What's an ultrafilter?  Well, lets define it for an arbitrary lattice.  The set, often called P(I), of subsets of any set I, is a lattice (the relevant ordering is subset inclusion, the defined meet and join are intersection and union).   A filter---not yet ultra---in a lattice is a subset of the lattice that is upward-closed, and meet-closed.  That is, to say that F is a filter is to say that  if x is in F, and y is greater than or equal to x, then y is in F, and that if x and y are both in f, so is x meet y.  For P(I), this means that a filter has to include every superset of each set in the filter, and also the intersection of every pair of sets in the filter.  Then we say a filter is proper if it's not the whole lattice, and it's an ultrafilter if it's a maximal proper filter, i.e. it's not properly contained in any other filter (other than the whole lattice).  A filter is called principal if it's generated by a single element of the lattice:  i.e. if it's the smallest filter containing that element.  Equivalently, it's the set consisting of that element and everything above it.  So in the case of P(I), a principal filter consists of a given set, and all sets containing that set.

To prove Arrow's theorem using ultrafilters, one shows that unanimity and IIA imply that the set of decisive sets is an ultrafilter on P(I).  But it was already well known, and is easy to show, that all ultrafilters on the powerset of a finite set are principal, and are generated by singletons of I, that is, sets containing single elements of I.  So a social choice rule satisfying unanimity and IIA has a decisive set containing a single element i, and furthermore, all sets containing i are decisive.  In other words, if i favors x over y, it doesn't matter who else favors x over y and who opposes it: x is socially preferred to y.  In other words, the rule is dictatorial.  QED.

Note that it is crucial here that the set I is finite.  If you assume the axiom of choice (no pun intended ahead of time), then non-principal ultrafilters do exist in the lattice of subspaces of an infinite set, and the more abstract-minded people who have thought about Arrow's theorem and ultrafilters have indeed noticed that if you are willing to generalize Arrow's conditions to an infinite electorate, whatever that means, the theorem doesn't generalize to that situation.  The standard existence proof for a non-principal ultrafilter is to use the axiom of choice in the form of Zorn's lemma to establish that any proper filter is contained in a maximal one (i.e. an ultrafilter) and then take the set of subsets whose complement (in I) is finite, show it's a filter, and show it's extension to an ultrafilter is not principal.  Just for fun, we'll do this in a later post.  I wouldn't summarize the situation by saying "infinite democracies exist", though.  As a sidelight, some people don't like the fact that the existence proof is nonconstructive.

As I said, I'll give the details in a later post.  Here, we want to examine Segre's proposed generalization.  He defines a quantum democracy  to be a nonprincipal ultrafilter on the lattice of projections of an "operator-algebraically finite von Neumann algebra".  In the preprint there's no discussion of motivation, nor are there explicit generalizations of unanimity and IIA to corresponding quantum notions.  To figure out such a correspondence for Segre's setup we'd need to convince ourselves that social choice rules, or ones satisfying one or the other of Arrow's properties, are related one to one to their sets of decisive coalitions, and then relate properties of the rule (or the remaining property), to the decisive coalitions' forming an ultrafilter.  Nonprincipality is clearly supposed to correspond to nondictatorship.  But I won't try to tease out, and then critique, a full correspondence right now, if one even exists.

Instead, let's look at Segre's main point.  He defines a quantum logic as a non-Boolean orthomodular lattice.  He defines a quantum democracy as a non-principal ultrafilter in a quantum logic.  His main theorem, IV.4, as stated, is that the set of quantum democracies is non-empty.  Thus stated, of course, it can be proved by showing the existence of even one quantum logic that has a non-principal ultrafilter.  These do exist, so the theorem is true.

However, there is nothing distinctively quantum about this fact.  Here, it's relevant that Segre's Theorem IV.3 as stated is wrong.  He states (I paraphrase to clarify scope of some quantifiers) that L is an operator-algebraically finite orthomodular lattice all of whose ultrafilters are principal if, and only if, L is a classical logic (i.e. a Boolean lattice).  But this is false.  It's true that to get his theorem IV.4, he doesn't need this equivalence.  But what is a von Neumann algebra?  It's a *-algebra consisting of bounded operators on a Hilbert space, closed in the weak operator topology.  (Or something isomorphic in the relevant sense to one of these.) There are commutative and noncommutative ones.  And there are finite-dimensional ones and infinite-dimensional ones.  The finite-dimensional ones include:  (1) the algebra of all bounded operators on a finite-dimensional Hilbert space (under operator multiplication and complex conjugation), these are noncommutative for dimension > 1  (2) the algebra of complex functions on a finite set I (under pointwise multiplication and complex conjugation) and (3) finite products (or if you prefer the term, direct sums) of algebras of these types.  (Actually we could get away with just type (1) and finite products since the type (2) ones are just finite direct sums of one-dimensional instances of type (1).)   The projection lattices of the cases (2) are isomorphic to P(I) for I the finite set.  These are the projection lattices for which Arrow's theorem can be proved using the fact that they have no nonprincipal ultrafilters.  The cases (1) are their obvious quantum analogues.  And it is easy to show that in these cases, too, there are no nonprincipal ultrafilters.  Because the lattice of projections of a von Neumann algebra is complete, one can use  essentially the same proof as for the case of P(I) for finite I.  So for the obvious quantum analogues of the setups where Arrow's theorem is proven, the analogue of Arrow's theorem does hold, and Segre's "quantum democracies" do not exist.

Moreover, Alex Wilce pointed out to me in email that essentially the same proof as for P(I) with I infinite, gives the existence of a nonprincipal ultrafilter for any infinite-dimensional von Neumann algebra:  one takes the set of projections of cofinite rank (i.e. whose orthocomplementary projection has finite rank), shows it's a filter, extends it (using Zorn's lemma) to an ultrafilter, and shows that's not principal.  So (if the dividing line between finite-dimensional and infinite-dimensional von Neumann algebras is precisely that their lowest-dimensional faithful representations are on finite-dimensional Hilbert spaces, which seems quite likely) the dividing line between projection lattices of von Neumann algebras on which Segre-style "democracies" (nonprincipal ultrafilters) exist, is precisely that between finite and infinite dimension, and not that between commutativity and noncommutativity.  I.e. the existence or not of a generalized decision rule satisfying a generalization of the conjunction of Arrow's conditions has nothing to do with quantumness.  (Not that I think it would mean much for social choice theory or voting if it did.)

(3) I'll only say a little bit here about "quantum psychology".  Some supposedly paradoxical empirical facts are described at the end of the article.  When subjects playing Prisoner's Dilemma are told that the other player will snitch, they always (nearly always? there must be a few mistakes...) snitch.  When they are told that the other player will stay mum, they usually also fink, but sometimes (around 20% of the time---it is not stated whether this typical of a single individual in repeated trials, or a percentage of individuals in single trials) stay mum.  However, if they are not told what the other player will do, "about 40% of the time" they stay mum.  Emanuel Pothos and Jerome Busemeyr devised a "quantum model" that reproduced the result.  As described in Sci Am, Pothos interprets it in terms of destructive interference between (amplitudes associated with, presumably) the 100% probability of snitching when the other snitches and the 80% probability of snitching when they other does not that reduces the probability to 60% when they are not sure whether the other will snitch.  It is a model; they do not claim that quantum physics of the brain is responsible.  However, I think there is a better explanation, in terms of what Douglas Hofstadter called "superrationality", Nigel Howard called "metarationality", and I like to call a Kantian equilibrium concept, after the version of Kant's categorial imperative that urges you to act according to a maxim that you could will to be a universal law.  Simply put, it's the line of reasoning that says "the other guy is rational like me, so he'll do what I do.  What does one do if he believes that?  Well, if we both snitch, we're sunk.  If we both stay mum, we're in great shape.  So we'll stay mum."  Is that rational?  I dunno.  Kant might have argued it is.  But in any case, people do consider this argument, as well, presumably, as the one for the Nash equilibrium.  But in either of the cases where the person is told what the other will do, there is less role for the categorical imperative; one is being put more in the Nash frame of mind.  Now it is quite interesting that people still cooperate a fair amount of the time when they know the other person is staying mum; I think they are thinking of the other person's action as the outcome of the categorical imperative reasoning, and they feel some moral pressure to stay with the categorical imperative reasoning.  Whereas they are easily swayed to completely dump that reasoning in the case when told the other person snitched: the other has already betrayed the categorical imperative.  Still, it is a bit paradoxical that people are more likely to cooperate when they are not sure whether the other person is doing so;  I think the uncertainty makes the story that "he will do what I do" more vivid, and the tempting benefit of snitching when the other stays mum less vivid, because one doesn't know *for sure* that the other has stayed mum.  Whether that all fits into the "quantum metaphor" I don't know but it seems we can get quite a bit of potential understanding here without invoking.  Moreover there probably already exists data to help explore some of these ideas, namely about how the same individual behaves under the different certain and uncertain conditions, in anonymous trials guaranteed not to involve repetition with the same opponent.

Less relevant to quantum theory, but perhaps relevant in assessing how important voting paradoxes are in the real world, is an entirely non-quantum point:

(4)  A claim by Piergiorgio Odifreddi, that the 1976 US election is an example of Condorcet's paradox of cyclic pairwise majority voting, is prima facie highly implausible to anyone who lived through that election in the US.  The claim is that a majority would have favored, in two-candidate elections:

Carter over Ford (as in the actual election)

Ford over Reagan

Reagan over Carter

I strongly doubt that Reagan would have beat Carter in that election.  There is some question of what this counterfactual means, of course:  using polls conducted near the time of the election does not settle the issue of what would have happened in a full general-election campaign pitting Carter against Reagan.  In "Preference Cycles in American Elections", Electoral Studies 13: 50-57 (1994), as summarized in Democracy Defended by Gerry Mackie, political scientist Benjamin Radcliff analyzed electoral data and previous studies concerning the US Presidential elections from 1972 through 1984, and found no Condorcet cycles.  In 1976, the pairwise orderings he found for (hypothetical, in two of the cases) two-candidate elections were Carter > Ford, Ford > Reagan, and Carter > Reagan.  Transitivity is satisfied; no cycle.  Obviously, as I've already discussed, there are issues of methodology, and how to analyze a counterfactual concerning a general election.  More on this, perhaps, after I've tracked down Odifreddi's article.  Odifreddi is in the Sci Am article because an article by him inspired Gavriel Segre to try to show that such problems with social choice mechanisms like voting might be absent in a quantum setting.

Odifreddi is cited by Musser as pointing out that democracies usually avoid Condorcet paradoxes because voters tend to line up on an ideological spectrum---I'm just sceptical until I see more evidence, that that was not the case also in 1976 in the US.  I have some doubt also about the claim that Condorcet cycles are the cause of democracy "becoming completely dysfunctional" in "politically unsettled times", or indeed that it does become completely dysfunctional in such times.  But I must remember that Odifreddi is from the land of Berlusconi.  But then again, I doubt cycles are the main issue with him...

Claimed proof of P not equal to NP by Vinay Deolalikar is being taken seriously

Posted on by

Via Richard Lipton, news that HP research scientist Vinay Deolalikar has put online a 102 page draft of a paper purporting to prove that P is not equal to NP.  (Follow the link to Deolalikar's page, and the paper is the first one linked under "Selected Publications".)  It is being taken seriously by serious people  (like Lipton)--- in the sense that they are trying to understand it and understand whether or not it is correct.   The length, of course, increases the likelihood of a so-far unspotted error.  Lipton thinks Deolalikar's use of finite model theory is an interesting and promising twist.  I have only just downloaded the paper, and am not a complexity theory expert, but what leaps out at me from the abstract is that it involves graphical models for sets of interacting random variables, an area that interests me.  Not that surprising, I guess, as lots of difficult problems---as well as ones that are easy but perhaps not obviously so, because of structure described by a graphical model of the dependencies between variables---are naturally described in graphical terms, and the relation between graphical models and complexity is a well-studied---though mostly relatively recently studied---topic.  I can no longer find the link to the online draft of Marc Mezard and Andrea Montanari's book on the subject (and its relations to physics and coding theory), perhaps because it's been published.  [Correction:  it's still online here.   Thanks to commenter Kristal Cantwell for the link.]  One key notion in such models is conditional independence---independence of two subsets of the random variables in question, when conditioned on a third set.  A really nice paper on a quantum notion of conditional independence, relating it to the equality conditions for the strong subadditivity inequality for quantum entropy, is by Hayden, Jozsa, Petz, and Winter.  Matt Leifer and David Poulin, and others, have described quantum graphical models.

You can bet that if Deolalikar's proof looks good, a slew of people will be applying the research strategy I like to call the "quantization functor" to it.

For those for whom P and NP are not their bread and butter, to give you an idea of how big this would be: I just goofed by telling my wife that if this pans out, it will be one of the most important results of twentieth century mathematics.  Well, it would have been if done in the twentieth century.  But I'll say more: although we're only 10 years in, I think it will be one of the most important results of twenty-first century mathematics.  I haven't said what it really means but that's what Wikipedia is for.

I should point out that Scott Aaronson is dubious, though not based on close perusal of the proof.  He has pledged to personally supplement the million dollars the Clay Mathematics Institute will pay Deolalikar if the proof is correct, with two hundred grand of his own.

Print-On-Demand publishing: will it allow academics to compete with major publishers?

Posted on by

Since I'm thinking of writing a scholarly book or two, I wonder whether print-on-demand publishing houses, combined with outlets like Amazon, allow academics to effectively compete directly with the more usual academic publishers like Springer, Cambridge UP, Oxford UP, etc...?  I've recently noticed that in ordering new books from all three of these publishers, I've frequently been sent what look like print-on-demand editions.  Here's a bit on Springer's POD activities.   To take one recent purchase, Faraut and Koranyi's Analysis on Symmetric Cones, Oxford, is now print-on-demand, and they're still charging $200 for it.  It's adequate, but much less attractive than the original edition which has the trademark Oxford deep-blue cloth-covered boards, with nicely finished paper (perhaps excessively sized, even) and extremely crisp type.  The print-on-demand edition is on paper that's not as nice, an almost inkjet-printed appearance where the edges of the characters are just not crisp enough for my taste, and the boards are thick, covered with something glossy, and more prone to warp outward so the book doesn't quite close firmly.  Springer and Cambridge POD books are similar.  It's a little more like you LaTeX'd something, printed it out two-pages-to-a-sheet, cut the sheets in half and glued them into a binding.  (Except maybe your average laser printer would produce sharper results---I'd need to do a direct comparison.)  This is quite serviceable for the right price, for usable math books, but $200 (I was able to find it for less, but still an outrageously high price) seems ridiculous.  But if academics were able to publish their works this way, sell for $40-65, deduct the cost of printing (about which I'm quite curious), do a little yearly accounting and extra business at tax time, and pocket the rest, it might be a much better deal than publishing through a major house.  I suspect that for a good academic work, reputation developed through citations and online access (one could make the book available chapter-by-chaper for free, if desired) might work almost as well as the publicity provided by an academic or corporate publisher.  The major issue might be library purchases, I'm guessing.  Anybody out there have any experience or ideas with this?

More info:  Amazon's POD printing and distribution unit, Createspace (Springer's US partner) has an expanded distribution plan claimed to wholesale books to libraries and bookstores.  Cambridge has partnered with LightningSource.

Here's a video of the Espresso Book Machine, for producing paperback books at or near the point of sale, in action:

Here's Amazon's "Pro Plan" at their CreateSpace. The combination of the terminology "royalties" for the money you get, and "self-publishing", seems, technically, contradictory.   Royalties are paid by a publisher for the right to publish and sell your book; if you were actually self-publishing, you would be hiring Amazon/Createspace to print your book, and do some of its distribution and sales, but what you keep would be profit, not royalties.  So I'm curious which it actually is, in their case.  Anyway, you seem to get about 43% of the list price on sales through Amazon, 23% on their Expanded Distribution Channel (to libraries, bookstores, and "certified resellers" at, presumably, wholesale prices, although maybe not since Amazon labels the entire difference between your share and list price "Our Share"), and 63% through something called an eStore (which is presumably an outlet at your own website, linked to Amazon; more investigation warranted).   Those are on a $16 book; on a $45, 320 page book with black and white interior, it looks like 30% through the EDC, 50% through Amazon, and 70% through your eStore.  I'm guessing this is for a paperback.

So, quite a bit better than the standard academic press royalty which I believe is something like 7% or so, but still, through the expanded distribution channel, not that hefty.

How does one prove that domains of positivity of symmetric nondegenerate bilinear forms are self-dual cones?

Posted on by

On mathoverflow, I've asked how one proves that domains of positivity of symmetric nondegenerate bilinear forms on real vector spaces are self-dual cones.  A bilinear form on a real vector space is just a map that is linear in each argument.  (In other words, if you fix , the function that takes to is linear, and similarly if you fix the other argument.)  It's called nondegenerate if the only such that for all , is .  And, of course, it's symmetric if for all , .

A closed domain of positivity of such a form is a maximal set such that .  Maximal means maximal in the ordering of sets by containment, i.e. is not contained in any other set satisfying .  This notion was introduced, or at least used, by Max Koecher in the late 1950s, in work that led to the celebrated result, published in 1958 in "The Geodesics of Domains of Positivity"  (well, actually, "Die Geodatische von Positivitatsbereichen" (Mathematische Annalen 135 (1958), pp. 192--202)), that homogeneous self-dual cones in finite dimension are precisely the cones of squares in finite-dimensional formally real (aka Euclidean) Jordan algebras.  Indeed, probably the very interpretation of the main result of that paper as concerning homogeneous self-dual cones relies on the identification of domains of positivity with self-dual cones that I'm looking for a proof of.

If the form were positive semidefinite, i.e. for all (which implies symmetry) then a domain of positivity for would clearly  be a self-dual cone.  This is practically the definition of a self-dual cone.  The dual of a cone in a real inner product space is the set of all vectors whose inner product with everything in the cone is nonnegative---and the definition of an inner product on a real vector space is that it's a nondegenerate positive semidefinite bilinear form.  A self-dual cone is one that's equal to its dual cone.

For our definition of domain of positivity, the form was required only to be symmetric, not necessarily also positive semidefinite.  Nevertheless, according to things I've read, its domains of positivity are self-dual cones.   These domains are not necessarily unique, of course, although they are maximal, i.e. no one of them contains another).  Although I have a vague recollection of having seen a proof that they are self-dual, I haven't been able to find the paper or come up with a proof.

It's easy to prove that such a domain is a pointed, convex, closed cone.  A natural way to prove that it is a self-dual cone would be to exhibit a positive semidefinite form , depending on and possibly also on , such that is a domain of positivity of .   An idea for how to do this involves the fact that such a form can be diagonalized: we can find a basis for the vector space such that the matrix with elements is diagonal, with diagonal elements .  The number of signs on the diagonal is the signature of the form.  A natural candidate for is the Euclidean inner product in the basis (i.e are the components of in this basis).  That is, we just change the 's to 's in the diagonal form of .

Nondegenerate symmetric bilinear forms are interesting for a variety of reasons.  One of them is that they are closely related to the metric structure on a pseudo-Riemannian manifold.  Something like the following is true: you specify such a form at each point of the manifold, in such a way that the forms at the various points are nicely related to each other, and you've specified the geometric structure of a pseudo-Riemannian manifold.  (One restriction here, I believe, is that the signature of the forms has to be the same everywhere; the forms also need to vary somewhat smoothly, in a manner I should look up and summarize, but not now.)  For example, in the general relativistic description of spacetime, the spacetime manifold has signature .  Or ; people use different conventions.  I'm attracted to , because the odd-one-out corresponds in relativity theory to time, and this way, the forward and backward light cones are the (only!) domains of positivity for the form.  I.e. the form is ; we have (here , etc...).  Interestingly, with the other choice of signature, the domains of positivity consist of spacelike vectors, and there is a continuum of them.  To get a picture of what's going on, consider one time and two space dimensions, with signature .  You can visualize this in , with the vertical axis as time (associated with the diagonal element of the form) and the horizontal planes for constant time as a spacelike plane.  If you rotate the 45 degree line between and say the axis, around the axis, you get the boundary of a double cone, the forward and backward light cones.  But similar cones pointing along any ray in the plane are clearly domains of positivity for the form.  I suspect lots of other cones---basically, any self-dual cone you can fit into the "conic doughnut" that is the closed complement of the double light-cone, i.e. into the spacelike (and null) vectors, are also domains of positivity for this form.

My main reason for interest in the problem isn't pseudo-Riemannian geometry, however.  More on the main reason later.  (It has to do with the Koecher result cited above).

If you found this problem first on mathoverflow, and you have the answer, please post your answer there, and link to it here if you feel like it; if you encountered it first here, please post the answer here indicating you encountered the problem here, and it would be nice if you'd also post it on mathoverflow indicating you found it on my blog.  We can have a little race between we happy few who read this blog, and the overflowing mathematicians.  I know who I'm betting on---your mission, readers, should you choose to accept it, and should any of you actually exist, is to prove me wrong!

(Thanks to Will Jagy, of MSRI, for noticing that I defined nondegeneracy wrong here at first: as requiring that the only for which is . This wrong definition, corrected above, of course says that the form has no nontrivial "isotropic" or "null" vectors (ones for which ). And we certainly don't want to assume that! Sorry about the slip-up, which I dont think affected anything else in the post.)