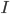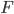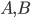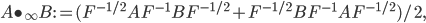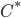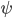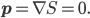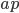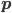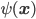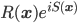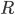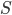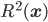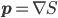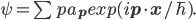Category Archives: Foundations of Quantum Theory

Anthony Aguirre is looking for postdoc at Santa Cruz in Physics of the Observer

Posted on by

Anthony Aguirre points out that UC Santa Cruz is advertising for postdocs in the "Physics of the Observer" program; and although review of applications began in December with a Dec. 15 deadline "for earliest consideration", if you apply fast you will still be considered.  He explicitly states they are looking for strong applicants from the quantum foundations community, among other things.

My take on this: The interaction of quantum and spacetime/gravitational physics is an area of great interest these days, and people doing rigorous work in quantum foundations, quantum information, general probabilistic theories have much to contribute.  It's natural to think about links with cosmology in this context.  I think this is a great opportunity, foundations postdocs and students, and Anthony and Max are good people to be connected with, very proactive in seeking out sources of funding for cutting-edge research and very supportive of interdisciplinary interaction.  The California coast around Santa Cruz is beautiful, SC is a nice funky town on the ocean, and you're within striking distance of the academic and venture capital powerhouses of the Bay Area.  So do it!

Martin Idel: the fixed-point sets of positive trace-preserving maps on quantum systems are Jordan algebras!

Posted on by

Kasia Macieszczak is visiting the ITP at Leibniz Universität Hannover (where I arrived last month, and where I'll be based for the next 7 months or so), and gave a talk on metastable manifolds of states in open quantum systems.  She told me about a remarkable result in the Master's thesis of Martin Idel at Munich: the fixed point set of any trace-preserving, positive (not necessarily completely positive) map on the space of Hermitian operators of a finite-dimensional quantum system, is a Euclidean Jordan algebra.  It's not necessarily a Jordan subalgebra of the usual Jordan algebra associated with the quantum system (whose Jordan product is the antisymmetrized matrix multiplication, ).  We use the usual characterization of the projector onto the fixed-point space of a linear map :  .  The maximum-rank fixed point is (where is the identity matrix), which we'll call , and the Jordan product on the fixed-point space is the original one "twisted" to have as its unit:  for fixed-points, this Jordan product, which I'll denote by , is:

which we could also write in terms of the original Jordan product as , where is the map defined by .

Idel's result, Theorem 6.1 in his thesis, is stated in terms of the map on all complex matrices, not just the  Hermitian ones; the fixed-point space is then the complexification of the Euclidean Jordan algebra.  In the case of completely positive maps, this complexification is "roughly a algebra" according to Idel.  (I suspect, but don't recall offhand, that it is a direct sum of full matrix algebras, i.e. isomorphic to a quantum system composed of several "superselection sectors" (the full matrix algebras in the sum), but as in the Euclidean case, not necessarily a -subalgebra of the ambient matrix algebra.)

I find this a remarkable result because I'm interested in places where Euclidean Jordan algebras appear in nature, or in mathematics.  One reason for this is that the finite-dimensional ones are in one-to-one correspondence with homogeneous, self-dual cones; perhaps I'll discuss this beautiful fact another time.  Alex Wilce, Phillip Gaebeler and I related the property of homogeneity to "steering" (which Schrödinger considered a fundamental weirdness of the newly developed quantum theory) in this paper.  I don't think I've blogged about this before, but Matthew Graydon, Alex Wilce, and I have developed ways of constructing composite systems of the general probabilistic systems based on reversible Jordan algebras, along with some results that I interpret as no-go theorems for such composites when one of the factors is not universally reversible.  The composites are still based on Jordan algebras, but are necessarily (if we wish them to still be Jordan-algebraic) not locally tomographic unless both systems are quantum.  Perhaps I'll post more on this later, too.  For now I just wanted to describe this cool result of Martin Idel's that I'm happy to have learned about today from Kasia.

ITFP, Perimeter: selective guide to talks. #1: Brukner on quantum theory with indefinite causal order

Posted on by

Excellent conference the week before last at Perimeter Institute: Information Theoretic Foundations for Physics.  The talks are online; herewith a selection of some of my favorites, heavily biased towards ideas new and particularly interesting to me (so some excellent ones that might be of more interest to you may be left off the list!).  Some of what would have been possibly of most interest and most novel to me happened on Weds., when the topic was spacetime physics and information, and I had to skip the day to work on a grant proposal.  I'll have to watch those online sometime.  This was going to be one post with thumbnail sketches/reviews of each talk, but as usual I can't help running on, so it may be one post per talk.

All talks available here, so you can pick and choose. Here's #1 (order is roughly temporal, not any kind of ranking...):

Caslav Brukner kicked off with some interesting work on physical theories in with indefinite causal structure.  Normally in formulating theories in an "operational" setting (in which we care primarily about the probabilities of physical processes that occur as part of a complete compatible set of possible processes) we assume a definite causal (partial) ordering, so that one process may happen "before" or "after" another, or "neither before nor after".  The formulation is "operational" in that an experimenter or other agent may decide upon, or at least influence, which set of processes, out of possible compatible sets, the actual process will be drawn, and then nature decides (but with certain probabilities for each possible process, that form part of our theory), which one actually happens.  So for instance, the experimenter decides to perform a Stern-Gerlach experiment with a particular orientation X of the magnets; then the possible processes are, roughly, "the atom was deflected in the X direction by an angle theta," for various angles theta.  Choose a different orientation, Y, for your apparatus, you choose a different set of possible compatible processes.  ("The atom was deflected in the Y direction by an angle theta.")  Then we assume that if one set of compatible processes happens after another, an agent's choice of which complete set of processes is realized later, can't influence the probabilities of processes occuring in an earlier set.  "No signalling from the future", I like to call this; in formalized operational theories it is sometimes called the "Pavia causality axiom".   Signaling from the past to the future is fine, of course.  If two complete  sets of processes are incomparable with respect to causal order ("spacelike-separated"), the no-signalling constraint operates both ways:  neither Alice's choice of which compatible set is realized, nor Bob's, can influence the probabilities of processes occuring at the other agent's site.   (If it could, that would allow nearly-instantaneous signaling between spatially separated sites---a highly implausible phenomenon only possible in preposterous theories such as the Bohmian version of quantum theory with "quantum disequilibrium", and Newtonian gravity. ) Anyway, Brukner looks at theories that are close to quantum, but in which this assumption doesn't necessarily apply: the probabilities exhibit "indeterminate causal structure".  Since the theories are close to quantum, they can be interpreted as allowing "superpositions of different causal structures", which is just the sort of thing you might think you'd run into in, say, theories combining features of quantum physics with features of general relativistic spacetime physics.  As Caslav points out, since in general relativity the causal structure is influenced by the distribution of mass and energy, you might hope to realize such indefinite causal structure by creating a quantum superposition of states in which a mass is in one place, versus being in another.  (There are people who think that at some point---some combinations of spatial scales (separation of the areas in which the mass is located) and mass scales (amount of mass to be separated in "coherent" superposition)) the possibility of such superpositions breaks down.  Experimentalists at Vienna (where Caslav---a theorist, but one who likes to work with experimenters to suggest experiments---is on the faculty) have created what are probably the most significant such superpositions.)

Situations with a superposition of causal orders seem to be exhibit some computational advantages over standard causally-ordered quantum computation, like being able to tell in fewer queries (one?) whether a pair of unitaries commutes or anticommutes.  Not sure whose result that was (Giulio Chiribella and others?), but Caslav presents some more recent results on query complexity in this model, extending the initial results.  I am generally wary about results on computation in theories with causal anomalies.  The stuff on query complexity with closed timelike curves, e.g. by Dave Bacon and by  Scott Aaronson and John Watrous has seemed uncompelling---not the correctness of the mathematical results, but rather the physical relevance of the definition of computation---to me for reasons similar to those given by Bennett, Leung, Smith and Smolin.  But I tend to suspect that Caslav and the others who have done these query results, use a more physically compelling framework because they are well versed in the convex operational or "general probabilistic theories" framework which aims to make the probabilistic behavior of processes consistent under convex combination ("mixture", i.e. roughly speaking letting somebody flip coins to decide which input to present your device with).  Inconsistency with respect to such mixing is part of the Bennett/Leung/Smolin/Smith objection to the CTC complexity classes as originally defined.

[Update:  This article at Physics.org quotes an interview with Scott Aaronson responding to the Bennett et. al. objections.  Reasonably enough, he doesn't think the question of what a physically relevant definition of CTC computing is has been settled.  When I try to think about this issue sometimes I wonder if the thorny philosophical question of whether we court inconsistency by trying to combine intervention ("free choice of inputs") in a physical theory is rearing its head.  As often with posts here, I'm reminding myself to revisit the issue at some point... and think harder.]

Quantum imaging with entanglement and undetected photons in Vienna

Posted on by
5

[Update 9/1:  I have been planning (before any comments, incidentally) to write a version of this post which just provides a concise verbal explanation of the experiment, supplemented perhaps with a little formal calculation.  However, I think the discussion below comes to a correct understanding of the experiment, and I will leave it up as an example of how a physicist somewhat conversant with but not usually working in quantum optics reads and quickly comes to a correct understanding of a paper.  Yes, the understanding is correct even if some misleading language was used in places, but I thank commenter Andreas for pointing out the latter.]

Thanks to tweeters @AtheistMissionary and @robertwrighter for bringing to my attention this experiment by a University of Vienna group (Gabriela Barreto Lemos, Victoria Borish, Garrett D. Cole, Sven Ramelo, Radek Lapkiewicz and Anton Zeilinger), published in Nature, on imaging using entangled pairs of photons.  It seems vaguely familiar, perhaps from my visit to the Brukner, Aspelmeyer and Zeilinger groups in Vienna earlier this year;  it may be that one of the group members showed or described it to me when I was touring their labs.  I'll have to look back at my notes.

This New Scientist summary prompts the Atheist and Robert to ask (perhaps tongue-in-cheek?) if it allows faster-than-light signaling.  The answer is of course no. The New Scientist article fails to point out a crucial aspect of the experiment, which is that there are two entangled pairs created, each one at a different nonlinear crystal, labeled NL1 and NL2 in Fig. 1 of the Nature article.  [Update 9/1: As I suggest parenthetically, but in not sufficiently emphatic terms, four sentences below, and as commenter Andreas points out,  there is (eventually) a superposition of an entangled pair having been created at different points in the setup; "two pairs" here is potentially misleading shorthand for that.] To follow along with my explanation, open the Nature article preview, and click on Figure 1 to enlarge it.  Each pair is coherent with the other pair, because the two pairs are created on different arms of an interferometer, fed by the same pump laser.  The initial beamsplitter labeled "BS1" is where these two arms are created (the nonlinear crystals come later). (It might be a bit misleading to say two pairs are created by the nonlinear crystals, since that suggests that in a "single shot" the mean photon number in the system after both nonlinear crystals  have been passed is 4, whereas I'd guess it's actually 2 --- i.e. the system is in a superposition of "photon pair created at NL1" and "photon pair created at NL2".)  Each pair consists of a red and a yellow photon; on one arm of the interferometer, the red photon created at NL1 is passed through the object "O".  Crucially, the second pair is not created until after this beam containing the red photon that has passed through the object is recombined with the other beam from the initial beamsplitter (at D2).  ("D" stands for "dichroic mirror"---this mirror reflects red photons, but is transparent at the original (undownconverted) wavelength.)  Only then is the resulting combination passed through the nonlinear crystal, NL2.  Then the red mode (which is fed not only by the red mode that passed through the object and has been recombined into the beam, but also by the downconversion process from photons of the original wavelength impinging on NL2) is pulled out of the beam by another dichroic mirror.  The yellow mode is then recombined with the yellow mode from NL1 on the other arm of the interferometer, and the resulting interference observed by the detectors at lower right in the figure.

It is easy to see why this experiment does not allow superluminal signaling by altering the imaged object, and thereby altering the image.  For there is an effectively lightlike or timelike (it will be effectively timelike, given the delays introduced by the beamsplitters and mirrors and such) path from the object to the detectors.  It is crucial that the red light passed through the object be recombined, at least for a while, with the light that has not passed through the object, in some spacetime region in the past light cone of the detectors, for it is the recombination here that enables the interference between light not passed through the object, and light passed through the object, that allows the image to show up in the yellow light that has not (on either arm of the interferometer) passed through the object.  Since the object must be in the past lightcone of the recombination region where the red light interferes, which in turn must be in the past lightcone of the final detectors, the object must be in the past lightcone of the final detectors.  So we can signal by changing the object and thereby changing the image at the final detectors, but the signaling is not faster-than-light.

Perhaps the most interesting thing about the experiment, as the authors point out, is that it enables an object to be imaged at a wavelength that may be difficult to efficiently detect, using detectors at a different wavelength, as long as there is a downconversion process that creates a pair of photons with one member of the pair at each wavelength.  By not pointing out the crucial fact that this is an interference experiment between two entangled pairs [Update 9/1: per my parenthetical remark above, and Andreas' comment, this should be taken as shorthand for "between a component of the wavefunction in which an entangled pair is created in the upper arm of the interferometer, and one in which one is created in the lower arm"], the description in New Scientist does naturally suggest that the image might be created in one member of an entangled pair, by passing the other member through the object,  without any recombination of the photons that have passed through the object with a beam on a path to the final detectors, which would indeed violate no-signaling.

I haven't done a calculation of what should happen in the experiment, but my rough intuition at the moment   is that the red photons that have come through the object interfere with the red component of the beam created in the downconversion process, and since the photons that came through the object have entangled yellow partners in the upper arm of the interferometer that did not pass through the object, and the red photons that did not pass through the object have yellow partners created along with them in the lower part of the interferometer, the interference pattern between the red photons that did and didn't pass through the object corresponds perfectly to an interference pattern between their yellow partners, neither of which passed through the object.  It is the latter that is observed at the detectors. [Update 8/29: now that I've done the simple calculation, I think this intuitive explanation is not so hot.  The phase shift imparted by the object "to the red photons" actually pertains to the entire red-yellow entangled pair that has come from NL1 even though it can be imparted by just "interacting" with the red beam, so it is not that the red photons interfere with the red photons from NL2, and the yellow with the yellow in the same way independently, so that the pattern could be observed on either color, with the statistical details perfectly correlated. Rather, without recombining the red photons with the beam, no interference could be observed between photons of a single color, be it red or yellow, because the "which-beam" information for each color is recorded in different beams of the other color.  The recombination of the red photons that have passed through the object with the undownconverted photons from the other output of the initial beamsplitter ensures that the red photons all end up in the same mode after crystal NL2 whether they came into the beam before the crystal or were produced in the crystal by downconversion, thereby ensuring that the red photons contain no record of which beam the yellow photons are in, and allowing the interference due to the phase shift imparted by the object to be observed on the yellow photons alone.]

As I mentioned, not having done the calculation, I don't think I fully understand what is happening.  [Update: Now that I have done a calculation of sorts, the questions raised in this paragraph are  answered in a further Update at the end of this post.  I now think that some of the recombinations of beams considered in this paragraph are not physically possible.]  In particular, I suspect that if the red beam that passes through the object were mixed with the downconverted beam on the lower arm of the interferometer after the downconversion, and then peeled off before detection, instead of having been mixed in before the downconversion and peeled off afterward, the interference pattern would not be observed, but I don't have clear argument why that should be.  [Update 8/29: the process is described ambiguously here.  If we could peel off the red photons that have passed through the object while leaving the ones that came from the downconversion at NL2, we would destroy the interference.  But we obviously can't do that; neither we nor our apparatus can tell these photons apart (and if we could, that would destroy interference anyway).  Peeling off *all* the red photons before detection actually would allow the interference to be seen, if we could have mixed back in the red photons first; the catch is that this mixing-back-in is probaby not physically possible.]  Anyone want to help out with an explanation?  I suspect one could show that this would be the same as peeling off the red photons from NL2 after the beamsplitter but before detection,  and only then recombining them with the red photons from the object, which would be the same as just throwing away the red photons from the object to begin with.  If one could image in this way, then that would allow signaling, so it must not work.  But I'd still prefer a more direct understanding via a comparison of the downconversion process with the red photons recombined before, versus after.  Similarly, I suspect that mixing in and then peeling off the red photons from the object before NL2 would not do the job, though I don't see a no-signaling argument in this case.  But it seems crucial, in order for the yellow photons to bear an imprint of interference between the red ones, that the red ones from the object be present during the downconversion process.

The news piece summarizing the article in Nature is much better than the one at New Scientist, in that it does explain that there are two pairs, and that the one member of one pair is passed through the object and recombined with something from the other pair.  But it does not make it clear that the recombination takes place before the second pair is created---indeed it strongly suggests the opposite:

According to the laws of quantum physics, if no one detects which path a photon took, the particle effectively has taken both routes, and a photon pair is created in each path at once, says Gabriela Barreto Lemos, a physicist at Austrian Academy of Sciences and a co-author on the latest paper.

In the first path, one photon in the pair passes through the object to be imaged, and the other does not. The photon that passed through the object is then recombined with its other ‘possible self’ — which travelled down the second path and not through the object — and is thrown away. The remaining photon from the second path is also reunited with itself from the first path and directed towards a camera, where it is used to build the image, despite having never interacted with the object.

Putting the quote from Barreta Lemos about a pair being created on each path before the description of the recombination suggests that both pair-creation events occur before the recombination, which is wrong. But the description in this article is much better than the New Scientist description---everything else about it seems correct, and it gets the crucial point that there are two pairs, one member of which passes through the object and is recombined with elements of the other pair at some point before detection, right even if it is misleading about exactly where the recombination point is.

[Update 8/28: clearly if we peel the red photons off before NL2, and then peel the red photons created by downconversion at NL2 off after NL2 but before the final beamsplitter and detectors, we don't get interference because the red photons peeled off at different times are in orthogonal modes, each associated with one of the two different beams of yellow photons to be combined at the final beamsplitter, so the interference is destroyed by the recording of "which-beam" information about the yellow photons, in the red photons. But does this mean if we recombine the red photons into the same mode, we restore interference? That must not be so, for it would allow signaling based on a decision to recombine or not in a region which could be arranged to be spacelike separated from the final beamsplitter and detectors.  But how do we see this more directly?  Having now done a highly idealized version of the calculation (based on notation like that in and around Eq. (1) of the paper) I see that if we could do this recombination, we would get interference.  But to do that we would need a nonphysical device, namely a one-way mirror, to do this final recombination.  If we wanted to do the other variant I discussed above, recombining the red photons that have passed the object with the red (and yellow) photons created at NL2 and then peeling all red photons off before the final detector, we would even need a dichroic one-way mirror (transparent to yellow, one-way for red), to recombine the red photons from the object with the beam coming from NL2.  So the only physical way to implement the process is to recombine the red photons that have passed through the object with light of the original wavelength in the lower arm of the interferometer before NL2; this just needs an ordinary dichroic mirror, which is a perfectly physical device.]

Free will and retrocausality at Cambridge II: Conspiracy vs. Retrocausality; Signaling and Fine-Tuning

Posted on by

Expect (with moderate probability) substantial revisions to this post, hopefully including links to relevant talks from the Cambridge conference on retrocausality and free will in quantum theory, but for now I think it's best just to put this out there.

Conspiracy versus Retrocausality

One of the main things I hoped to straighten out for myself at the conference on retrocausality in Cambridge was whether the correlation between measurement settings and "hidden variables" involved in a retrocausal explanation of Bell-inequality-violating quantum correlations are necessarily "conspiratorial", as Bell himself seems to have thought.  The idea seems to be that correlations between measurement settings and hidden variables must be due to some "common cause" in the intersection of the backward light cones of the two.  That is, a kind of "conspiracy" coordinating the relevant hidden variables that can affect the meausrement outcome with all sorts of intricate processes that can affect which measurement is made, such as those affecting your "free" decision as to how to set a polarizer, or, in case you set up a mechanism to control the polarizer setting according to some apparatus reasonably viewed as random ("the Swiss national lottery machine" was the one envisioned by Bell), the functioning of this mechanism.  I left the conference convinced once again (after doubts on this score had been raised in my mind by some discussions at New Directions in the Philosophy of Physics 2013) that the retrocausal type of explanation Price has in mind is different from a conspiratorial one.

Deflationary accounts of causality: their impact on retrocausal explanation

Distinguishing "retrocausality" from "conspiratorial causality" is subtle, because it is not clear that causality makes sense as part of a fundamental physical theory.   (This is a point which, in this form, apparently goes back to Bertrand Russell early in this century.  It also reminds me of David Hume, although he was perhaps not limiting his "deflationary" account of causality to causality in physical theories.)  Causality might be a concept that makes sense at the fundamental level for some types of theory, e.g. a version ("interpretation") of quantum theory that takes measurement settings and outcomes as fundamental, taking an "instrumentalist" view of the quantum state as a means of calculating outcome probabilities giving settings, and not as itself real, without giving a further formal theoretical account of what is real.  But in general, a theory may give an account of logical implications between events, or more generally, correlations between them, without specifying which events cause, or exert some (perhaps probabilistic) causal influence on others.  The notion of causality may be something that is emergent, that appears from the perspective of beings like us, that are part of the world, and intervene in it, or model parts of it theoretically.  In our use of a theory to model parts of the world, we end up taking certain events as "exogenous".  Loosely speaking, they might be determined by us agents (using our "free will"), or by factors outside the model.  (And perhaps "determined" is the wrong word.)   If these "exogenous" events are correlated with other things in the model, we may speak of this correlation as causal influence.  This is a useful way of speaking, for example, if we control some of the exogenous variables:  roughly speaking, if we believe a model that describes correlations between these and other variables not taken as exogenous, then we say these variables are causally influenced by the variables we control that are correlated with them.  We find this sort of notion of causality valuable because it helps us decide how to influence those variables we can influence, in order to make it more likely that other variables, that we don't control directly, take values we want them to.  This view of causality, put forward for example in Judea Pearl's book "Causality", has been gaining acceptance over the last 10-15 years, but it has deeper roots.  Phil Dowe's talk at Cambridge was an especially clear exposition of this point of view on causality (emphasizing exogeneity of certain variables over the need for any strong notion of free will), and its relevance to retrocausality.

This makes the discussion of retrocausality more subtle because it raises the possibility that a retrocausal and a conspiratorial account of what's going on with a Bell experiment might describe the same correlations, between the Swiss National lottery machine, or whatever controls my whims in setting a polarizer, all the variables these things are influenced by, and the polarizer settings and outcomes in a Bell experiment, differing only in the causal relations they describe between these variables.  That might be true, if a retrocausalist decided to try to model the process by which the polarizer was set.  But the point of the retrocausal account seems to be that it is not necessary to model this to explain the correlations between measurement results.  The retrocausalist posits a lawlike relation of correlation between measurement settings and some of the hidden variables that are in the past light cone of both measurement outcomes.  As long as this retrocausal influence does not influence observable past events, but only the values of "hidden", although real, variables, there is nothing obviously more paradoxical about imagining this than about imagining----as we do all the time---that macroscopic variables that we exert some control over, such as measurement settings, are correlated with things in the future.   Indeed, as Huw Price has long (I have only recently realized for just how long) been pointing out, if we believe that the fundamental laws of physics are symmetric with respect to time-reversal, then it would be the absence of retrocausality, if we dismiss its possibility, and even if we accept its possibility to the limited extent needed to potentially explain Bell correlations, its relative scarcity, that needs explaining.  Part of the explanation, of course, is likely that causality, as mentioned above, is a notion that is useful for agents situated within the world, rather than one that applies to the "view from nowhere and nowhen" that some (e.g. Price, who I think coined the term "nowhen") think is, or should be,  taken by fundamental physical theories.  Therefore whatever asymmetries---- these could be somewhat local-in-spacetime even if extremely large-scale, or due to "spontaneous" (i.e. explicit, even if due to a small perturbation) symmetry-breaking --- are associated with our apparently symmetry-breaking experience of directionality of time may also be the explanation for why we introduce the causal arrows we do into our description, and therefore why we so rarely introduce retrocausal ones.  At the same time, such an explanation might well leave room for the limited retrocausality Price would like to introduce into our description, for the purpose of explaining Bell correlations, especially because such retrocausality does not allow backwards-in-time signaling.

Signaling (spacelike and backwards-timelike) and fine-tuning. Emergent no-signaling?

A theme that came up repeatedly at the conference was "fine-tuning"---that no-spacelike-signaling, and possibly also no-retrocausal-signaling, seem to require a kind of "fine-tuning" from a hidden variable model that uses them to explain quantum correlations.  Why, in Bohmian theory, if we have spacelike influence of variables we control on physically real (but not necessarily observable) variables, should things be arranged just so that we cannot use this influence to remotely control observable variables, i.e. signal?  Similarly one might ask why, if we have backwards-in-time influence of controllable variables on physically real variables, things are arranged just so that we cannot use this influence to remotely control observable variables at an earlier time?  I think --- and I think this possibility was raised at the conference --- that a possible explanation, suggested by the above discussion of causality, is that for macroscopic agents such as us, with usually-reliable memories, some degree of control over our environment and persistence over time, to arise, it may be necessary that the scope of such macroscopic "observable" influences be limited, in order that there be a coherent macroscopic story at all for us to tell---in order for us even be around to wonder about whether there could be such signalling or not.  (So the term "emergent no-signalling" in the section heading might be slightly misleading: signalling, causality, control, and limitations on signalling might all necessarily emerge together.) Such a story might end up involving thermodynamic arguments, about the sorts of structures that might emerge in a metastable equilibrium, or that might emerge in a dynamically stable state dependent on a temperature gradient, or something of the sort.  Indeed, the distribution of hidden variables (usually, positions and/or momenta) according to the squared modulus of the wavefunction, which is necessary to get agreement of Bohmian theory with quantum theory and also to prevent signaling (and which does seem like "fine-tuning" inasmuch as it requires a precise choice of probability distribution over initial conditions), has on various occasions been justified by arguments that it represents a kind of equilibrium that would be rapidly approached even if it did not initially obtain.  (I have no informed view at present on how good these arguments are, though I have at various times in the past read some of the relevant papers---Bohm himself, and Sheldon Goldstein, are the authors who come to mind.)

I should mention that at the conference the appeal of such statistical/thermodynamic  arguments for "emergent" no-signalling was questioned---I think by Matthew Leifer, who with Rob Spekkens has been one of the main proponents of the idea that no-signaling can appear like a kind of fine-tuning, and that it would be desirable to have a model which gave a satisfying explanation of it---on the grounds that one might expect "fluctuations" away from the equilibria, metastable structures, or steady states, but we don't observe small fluctuations away from no-signalling---the law seems to hold with certainty.  This is an important point, and although I suspect there are  adequate rejoinders, I don't see at the moment what these might be like.

Free will and retrocausality in the quantum world, at Cambridge. I: Bell inequalities and retrocausality

Posted on by

I'm in Cambridge, where the conference on Free Will and Retrocausality in the Quantum World, organized (or rather, organised) by Huw Price and Matt Farr will begin in a few hours.  (My room at St. Catherine's is across from the chapel, and I'm being serenaded by a choir singing beautifully at a professional level of perfection and musicality---I saw them leaving the chapel yesterday and they looked, amazingly, to be mostly junior high school age.)  I'm hoping to understand more about how "retrocausality", in which effects occur before their causes, might help resolve some apparent problems with quantum theory, perhaps in ways that point to potentially deeper underlying theories such as a "quantum gravity". So, as much for my own use as anyone else's, I thought perhaps I should post about my current understanding of this possibility.

One of the main problems or puzzles with quantum theory that Huw and others (such as Matthew Leifer, who will be speaking) think retrocausality may be able to help with, is the existence of Bell-type inequality violations. At their simplest, these involve two spacelike-separated regions of spacetime, usually referred to as "Alice's laboratory" and "Bob's laboratory", at each of which different possible experiments can be done. The results of these experiments can be correlated, for example if they are done on a pair of particles, one of which has reached Alice's lab and the other Bob's, that have previously interacted, or were perhaps created simultaneously in the same event. Typically in actual experiments, these are a pair of photons created in a "downconversion" event in a nonlinear crystal.  In a "nonlinear"  optical process photon number is not conserved (so one can get a "nonlinearity" at the level of a Maxwell's equation where the intensity of the field is proportional to photon number; "nonlinearity" refers to the fact that the sum of two solutions is not required to be a solution).  In parametric downconversion, a photon is absorbed by the crystal which emits a pair of photons in its place, whose energy-momentum four-vectors add up to that of the absorbed photon (the process does conserve energy-momentum).   Conservation of angular momentum imposes correlations between the results of measurements made by "Alice" and "Bob" on the emitted photons. These are correlated even if the measurements are made sometime after the photons have separated far enough that the changes in the measurement apparatus that determine which component of polarization it measures (which we'll henceforth call the "polarization setting"), on one of the photons, are space-like separated from the measurement process on the other photon, so that effects of the polarization setting in Alice's laboratory, which one typically assumes can propagate only forward in time, i.e. in their forward light-cone, can't affect the setting or results in Bob's laboratory which is outside of this forward light-cone.  (And vice versa, interchanging Alice and Bob.)

Knowledge of how their pair of photons were prepared (via parametric downconversion and propagation to Alice and Bob's measurement sites) is encoded in a "quantum state" of the polarizations of the photon pair.  It gives us, for any pair of polarization settings that could be chosen by Alice and Bob, an ordinary classical joint probability distribution over the pair of random variables that are the outcomes of the given measurements.  We have different classical joint distributions, referring to different pairs of random variables, when different pairs of polarization settings are chosen.   The Bell "paradox" is that there is no way of introducing further random variables that are independent of these polarization settings, such that for each pair of polarization settings, and each assignment of values to the further random variables, Alice and Bob's measurement outcomes are independent of each other, but when the further random variables are averaged over, the experimentally observed correlations, for each pair of settings, are reproduced. In other words, the outcomes of the polarization measurements, and in particular the fact that they are correlated, can't be "explained" by variables uncorrelated with the settings. The nonexistence of such an explanation is implied by the violation of a type of inequality called a "Bell inequality". (It's equivalent to to such a violation, if "Bell inequality" is defined generally enough.)

How I stopped worrying and learned to love quantum correlations

One might have hoped to explain the correlations by having some physical quantities (sometimes referred to as "hidden variables") in the intersection of Alice and Bob's backward light-cone, whose effects, propagating forward in their light-cone to Alice and Bob's laboratories, interact their with the physical quantities describing the polarization settings to produce---whether deterministically or stochastically---the measurement outcomes at each sites, with their observed probabilities and correlations. The above "paradox" implies that this kind of "explanation" is not possible.

Some people, such as Tim Maudlin, seem to think that this implies that quantum theory is "nonlocal" in the sense of exhibiting some faster-than-light influence. I think this is wrong. If one wants to "explain" correlations by finding---or hypothesizing, as "hidden variables"---quantities conditional on which the probabilities of outcomes, for all possible measurement settings, factorize, then these cannot be independent of measurement settings. If one further requires that all such quantities must be localized in spacetime, and that their influence propagates (in some sense that I'm not too clear about at the moment, but that can probably be described in terms of differential equations---something like a conserved probability current might be involved) locally and forward in time, perhaps one gets into inconsistencies. But one can also just say that these correlations are a fact. We can have explanations of these sorts of fact---for example, for correlations in photon polarization measurements, the one alluded to above in terms of energy-momentum conservation and previous interaction or simultaneous creation---just not the sort of ultra-classical one some people wish for.

Retrocausality

It seems to me that what the retrocausality advocates bring to this issue is the possibility of something that is close to this type of classical explanation. It may allow for the removal of these types of correlation by conditioning on physical quantities. [Added July 31: this does not conflict with Bell's theorem, for the physical quantities are not required to be uncorrelated with measurement settings---indeed, being correlated with the measurement settings is to be expected if there is retrocausal influence from a measurement setting to physical quantities in the backwards light-cone of the measurement setting.] And unlike the Bohmian hidden variable theories, it hopes to avoid superluminal propagation of the influence of measurement settings to physical quantities, even unobservable ones.  It does this, however, by having the influence of measurement settings pursue a "zig-zag" path from Alice to Bob: in Alice's backward light-cone back to the region where Alice and Bob's backward light-cones intersect, then forward to Bob's laboratory. What advantages might this have over superluminal propagation? It probably satisfies some kind of spacetime continuity postulate, and seems more likely to be able to be Lorentz-invariant. (However, the relation between formal Lorentz invariance and lack of superluminal propagation is subtle, as Rafael Sorkin reminded me at breakfast today.)

Bohm on measurement in Bohmian quantum theory

Posted on by

Prompted, as described in the previous post, by Craig Callender's post on the uncertainty principle, I've gone back to David Bohm's original series of two papers "A suggested interpretation of the quantum theory in terms of "hidden" variables I" and "...II", published in Physical Review in 1952 (and reprinted in Wheeler and Zurek's classic collection "Quantum Theory and Measurement", Princeton University Press, 1983).  The Bohm papers and others appear to be downloadable here.

Question 1 of my previous post asked whether it is true that

"a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus."

It is fairly clear from Bohm's papers that the answer is "Yes". In section 5 of the second paper, he writes

"in the measurement of an "observable," Q, we cannot obtain enough information to provide a complete specification of the state of an electron, because we cannot infer the precisely defined values of the particle momentum and position, which are, for example, needed if we wish to make precise predictions about the future behavior of the electron. [...] the measurement of an "observable" is not really a measurement of any physical property belonging to the observed system alone. Instead, the value of an "observable" measures only an incompletely predictable and controllable potentiality belonging just as much to the measuring apparatus as to the observed system itself."

Since the first sentence quoted says we cannot infer precise values of "momentum and position", it is possible to interpret it as referring to an uncertainty-principle-like tradeoff of precision in measurement of one versus the other, rather than a statement that it is not possible to measure either precisely, but I think that would be a misreading, as the rest of the quote, which clearly concerns any single observable, indicates. Later in the section, he unambiguously gives the answer "Yes" to a mutation of my Question 1 which substitutes momentum for position. Indeed, most of the section is concerned with using momentum measurement as an example of the general principle that the measurements described by standard quantum theory, when interpreted in his formalism, do not measure pre-existing properties of the measured system.

Here's a bit of one of two explicit examples he gives of momentum measurement:

"...consider a stationary state of an atom, of zero angular momentum. [...] the -field for such a state is real, so that we obtain

Thus, the particle is at rest. Nevertheless, we see from (14) and (15) that if the momentum "observable" is measured, a large value of this "observable" may be obtained if the -field happens to have a large fourier coefficient, , for a high value of . The reason is that in the process of interaction with the measuring apparatus, the -field is altered in such a way that it can give the electron particle a correspondingly large momentum, thus transferring some of the potential energy of interaction of the particle with its -field into kinetic energy."

Note that the Bohmian theory involves writing the complex-valued wavefunction as , i.e. in terms of its (real) modulus and (real) phase . Expressing the Schrödinger equation in terms of these variables is in fact probably what suggested the interpretation, since one gets something resembling classical equations of motion, but with a term that looks like a potential, but depends on . Then one takes these classical-like equations of motion seriously, as governing the motions of actual particles that have definite positions and momenta. In order to stay in agreement with quantum theory concerning observed events such as the outcomes of measurements, m theory, one in addition keeps, from quantum theory, the assumption that the wavefunction evolves according to the Schrödinger equation. And one assumes that we don't know the particles' exact position but only that this is distributed with probability measure given (as quantum theory would predict for the outcome of a position measurement) by , and that the momentum is . That's why the real-valuedness of the wavefunction implies that momentum is zero: because the momentum, in Bohmian theory, is the gradient of the phase of the wavefunction.

For completeness we should reproduce Bohm's (15).

(15)

At least in the Wheeler and Zurek book, the equation has instead of as the subscript on , and instead of ; I consider these typos, and have corrected them. (Bohm's reference to (14), which is essentially the same as (15) seems to me to be redundant.)

The upshot is that

"the actual particle momentum existing before the measurement took place is quite different from the numerical value obtained for the momentum "observable,"which, in the usual interpretation, is called the "momentum." "

It would be nice to have this worked out for a position measurement example, as well. The nicest thing, from my point of view, would be an example trajectory, for a definite initial position, under a position-measurement interaction, leading to a final position different from the initial one. I doubt this would be too hard, although it is generally considered to be the case that solving the Bohmian equations of motion is difficult in the technical sense of complexity theory. I don't recall just how difficult, but more difficult than solving the Schrödinger equation, which is sometimes taken as an argument against the Bohmian interpretation: why should nature do all that work, only to reproduce, because of the constraints mentioned above---distribution of according to , ---observable consequences that can be more easily calculated using the Schrödinger equation?
I think I first heard of this complexity objection (which is of course something of a matter of taste in scientific theories, rather than a knockdown argument) from Daniel Gottesman, in a conversation at one of the Feynman Fests at the University of Maryland, although Antony Valentini (himself a Bohmian) has definitely stressed the ability of Bohmian mechanics to solve problems of high complexity, if one is allowed to violate the constraints that make it observationally indistinguishable from quantum theory. It is clear from rereading Bohm's 1952 papers that Bohm was excited about the physical possibility of going beyond these constraints, and thus beyond the limitations of standard quantum theory, if his theory was correct.

In fairness to Bohmianism, I should mention that in these papers Bohm suggests that the constraints that give standard quantum behavior may be an equilibrium, and in another paper he gives arguments in favor of this claim. Others have since taken up this line of argument and done more with it. I'm not familiar with the details. But the analogy with thermodynamics and statistical mechanics breaks down in at least one respect, that one can observe nonequilibrium phenomena, and processes of equilibration, with respect to standard thermodynamics, but nothing like this has so far been observed with respect to Bohmian quantum theory. (Of course that does not mean we shouldn't think harder, guided by Bohmian theory, about where such violations might be observed... I believe Valentini has suggested some possibilities in early-universe physics.)

A question about measurement in Bohmian quantum mechanics

Posted on by

I was disturbed by aspects of Craig Callender's post "Nothing to see here," on the uncertainty principle, in the New York Times' online philosophy blog "The Stone," and I'm pondering a response, which I hope to post here soon.  But in the process of pondering, some questions have arisen which I'd like to know the answers to.  Here are a couple:

Callender thinks it is important that quantum theory be formulated in a way that does not posit measurement as fundamental.  In particular he discusses the Bohmian variant of quantum theory (which I might prefer to describe as an alternative theory) as one of several possibilities for doing so.  In this theory, he claims,

Uncertainty still exists. The laws of motion of this theory imply that one can’t know everything, for example, that no perfectly accurate measurement of the particle’s velocity exists. This is still surprising and nonclassical, yes, but the limitation to our knowledge is only temporary. It’s perfectly compatible with the uncertainty principle as it functions in this theory that I measure position exactly and then later calculate the system’s velocity exactly.

While I've read Bohm's and Bell's papers on the subject, and some others, it's been a long time in most cases, and this theory is not something I consider very promising as physics even though it is important as an illustration of what can be done to recover quantum phenomena in a somewhat classical theory (and of the weird properties one can end up with when one tries to do so).  So I don't work with it routinely.  And so I'd like to ask anyone, preferably more expert than I am in technical aspects of the theory, though not necessarily a de Broglie-Bohm adherent, who can help me understand the above claims, in technical or non-technical terms, to chime in in the comments section.

I have a few specific questions.  It's my impression that in this theory, a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus.

Question 1:  Is that correct?

A little more discussion of Question 1.  On my understanding, what is claimed is, rather, something like: that if one has a probability distribution over particle positions and momenta and a "pilot wave" (quantum wave function) whose squared amplitude agrees with these distributions (is this required in both position and momentum space? I'm guessing so), then the probability (calculated using the distribution over initial positions and momenta, and the deterministic "laws of motion" by which these interact with the "pilot wave" and the apparatus) for the apparatus to end up showing position in a given range, is the same as the integral of the squared modulus of the wavefunction, in the position representation, over that range.  Prima facie, this could be achieved in ways other than having the measurement reading being perfectly correlated with the initial position on a given trajectory, and my guess is that in fact it is not achieved in that way in the theory.    If that were so it seems like the correlation should hold whatever the pilot wave is.  Now, perhaps that's not a problem, but it makes the pilot wave feel a bit superfluous to me, and I know that it's not, in this theory.  My sense is that what happens is more like:  whatever the initial position is, the pilot wave guides it to some---definite, of course---different final position, but when the initial distribution is given by the squared modulus of the pilot wave itself, then the distribution of final positions is given by the squared modulus of the (initial, I guess) pilot wave.

But if the answer to question 1 is "Yes", I have trouble understanding what Callender means by "I measure position exactly".  Also, regardless of the answer to Question 1, either there is a subtle distinction being made between measuring "perfectly accurately" and measuring "exactly" (in which case I'd like to know what the distinction is), or these sentences need to be reformulated more carefully.  Not trying to do a gotcha on Callender here, just trying to understand the claim, and de Broglie Bohm.

My second question relates to Callender's statement that:

It’s perfectly compatible with the uncertainty principle as it functions in this theory that I measure position exactly and then later calculate the system’s velocity exactly

Question 2: How does this way of ascertaining the system's velocity differ from the sort of "direct measurement" that is, presumably, subject to the uncertainty principle? I'm guessing that by the time one has enough information (possibly about further positions?) to calculate what the velocity was, one can't do with it the sorts of things that one could have done if one had known the position and velocity simultaneously.  But this depends greatly on what it would mean to "have known" the position and/or velocity, which --- especially if the answer to Question 1 was "Yes"--- seems a rather subtle matter.

So, physicists and other readers knowledgeable on these matters (if any such exist), your replies with explanations, or links to explanations, of these points would be greatly appreciated.  And even if you don't know the answers, but know de Broglie-Bohm well on a technical level... let's figure this out!  (My guess is that it's well known, and indeed that the answer to Question 1 in particular is among the most basic things one learns about this interpretation...)

My short review of David Deutsch's "The Beginning of Infinity" in Physics Today

Posted on by

Here is a link to my short review of David Deutsch's book The Beginning of Infinity, in Physics Today, the monthly magazine for members of the American Physical Society.  I had much more to say about the book, which is particularly ill-suited to a short-format review like those in Physics Today.  (The title is suggestive; and a reasonable alternative would have been "Life, the Universe, and Everything.")   It was an interesting exercise to boil it down to this length, which was already longer than their ideal.  I may say some of it in a blog post later.

It was also interesting to have such extensive input from editors.  Mostly this improved things, but in a couple of cases (not helped by my internet failing just as the for-publication version had been produced) the result was not good.  In particular, the beginning of the second-to-last paragraph, which reads "For some of Deutsch’s concerns, prematurity is irrelevant. But fallibilism undermines some of his claims ... " is not as I'd wanted.  I'd had "this" in place of "prematurity" and "it" in place of "fallibilism".  I'd wanted, in both cases, to refer in general to the immediately preceding discussion, more broadly than just to "prematurity" in one case and "fallibilism" in the other.  It seems the editors felt uncomfortable with a pronoun whose antecedent was not extremely specific.  I'd have to go back to notes to see what I ultimately agreed to, but definitely not plain "prematurity".

One other thing I should perhaps point out is that when I wrote:

Deutsch’s view that objective correctness is possible in areas outside science is appealing. And his suggestion that Popperian explanation underwrites that possibility is intriguing, but may overemphasize the importance of explanations as opposed to other exercises of reason. A broader, more balanced perspective may be found in the writings of Roger Scruton, Thomas Nagel, and others.

I was referring to a broader perspective on the role of reason in arriving at objectively correct views in areas outside science. "More balanced" was another editorial addition, in this case one that I acquiesced in, but perhaps I should not have as some of its possible connotations are more negative than I intended.  "Appealing," though not an editorial edition, is somewhat off from what I intended.  I wanted also to include suggestion of "probably correct" since something can be appealing but wrong, but couldn't find the right word.  I shortened this discussion for reasons of space, but I had initially cited Scruton specifically for aesthetics, and recommended his "On Beauty", "Art and the Imagination", and "The Aesthetics of Architecture".  I haven't read much of his work on politics (he is a conservative, although from what I have read a relatively sensible one at the philosophical level) nor his "Sexual Desire", so don't mean to endorse them.  Likewise I had initially recommended specifically Nagel's "The View from Nowhere" and "The Last Word", and was not aware of his recent "Mind and Cosmos"; I emphatically did not mean to endorse his skepticism, in that book, about evolutionary explanations of the origins of life and mind, although I do think there is much of interest in that book, and some (but certainly not all!) of the criticism of it that I've seen on the web is misguided.  I am much more in sympathy with Deutsch's views on reductionism than with Nagel's:  both are skeptical about the prospects for a thoroughoing reduction of mind, reason, and consciousness to physical terms, but Nagel, bafflingly, seems to think that an evolutionary explanation of such phenomena is tantamount to such physical reductionism.  Deutsch seems to me more sophisticated about the nature of actual science, and how non-reductionist many scientific explanations are, and about how that can nevertheless be compatible with physical law.  I should say, though, that I am less sympathetic than Deutsch is to accounts of mind and consciousness as being essentially a computer running a certain kind of program.  I view embodiment, interaction with a sufficiently rich environment, and probably a difficulty in disentangling "hardware" and "software" (perhaps related to Douglas Hofstadter's notion of "strange loops") as likely to be crucial elements of an understanding of mind and consciousness.  Of course it may be that with a sufficiently loose notion of "kind of computer program" and "kind of input" some of this could be understood in the computational terms Deutsch seeks.

Physics and philosophy: a civil and enlightening discussion

Posted on by

So, more on physics and philosophy:  this discussion thread involving Wayne Myrvold, Vishnya Maudlin, and Matthew Leifer is a model of civil discussion in which it looks like mutual understanding is increased, and that should be enlightening, or at least clarifying, to "listeners".  Matthew makes a point I made in my previous post:

Matthew Leifer [...] Wayne, I disagree with you that studying the foundations of quantum theory is philosophy. It is physics, it is just that most physicists do not realize that it is physics yet. Of course, there are some questions of a more philosophical nature, but I would argue that the most fertile areas are those which are not obviously purely philosophy.

Wayne Myrvold (June 12 at 6:42am)

Ah, but Matt, but part of the main point of the post was that we shouldn’t worry too much about where we draw the boundaries between disciplines. It’s natural philosophy in the sense of Newton, not counted as physics by many physicists, and may one day will be regarded as clearly part of physics by the physics community—- does it really matter what we call it? [...]

Matthew's response: "Well, it matters a lot on a personal level if you are trying to get a job doing foundations of quantum theory in a physics department 🙂 More seriously, I think there is a distinction to be made between studying the foundations of a theory in order to better comprehend the theory as it presently exists and studying them in order to arrive at the next theory."

Matthew puts a smiley face on the first sentence, and continues "More seriously..." But I think this is more serious than he is letting on here. In my view, thinking about M-theory and string theory and thinking about the foundations of quantum theory are roughly evenly matched as far as their likelihood (by which I mean probability) of giving rise to genuine progress in our understanding of the world (I'd give quantum foundations the advantage by about a factor of 10.) In fact, thinking about quantum foundations led David Deutsch to come up with what is pretty much our present concept of universal quantum computation. Yet you basically can't do it in a US physics department without spending much of your time on something else in order to get tenure. This is part of why I'm not just annoyed, but more like outraged, when I read pronouncements like Hawking's about philosophy being dead.

As with Wayne's post on which this thread comments, I thank Matthew Leifer for the link to this thread. Do read the whole thing if you find this topic area at all interesting as there are several other excellent and clearly expressed insights in it.