Kasia Macieszczak is visiting the ITP at Leibniz Universität Hannover (where I arrived last month, and where I'll be based for the next 7 months or so), and gave a talk on metastable manifolds of states in open quantum systems.  She told me about a remarkable result in the Master's thesis of Martin Idel at Munich: the fixed point set of any trace-preserving, positive (not necessarily completely positive) map on the space of Hermitian operators of a finite-dimensional quantum system, is a Euclidean Jordan algebra.  It's not necessarily a Jordan subalgebra of the usual Jordan algebra associated with the quantum system (whose Jordan product is the antisymmetrized matrix multiplication, 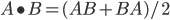).  We use the usual characterization of the projector 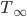onto the fixed-point space of a linear map 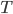:  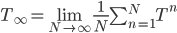.  The maximum-rank fixed point is 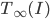(where 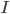is the identity matrix), which we'll call 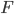, and the Jordan product on the fixed-point space is the original one "twisted" to have 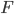as its unit:  for 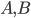fixed-points, this Jordan product, which I'll denote by , is:

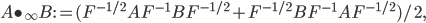
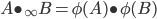which we could also write in terms of the original Jordan product as , where 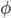is the map defined by .

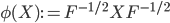Idel's result, Theorem 6.1 in his thesis, is stated in terms of the map on all complex matrices, not just the  Hermitian ones; the fixed-point space is then the complexification of the Euclidean Jordan algebra.  In the case of completely positive maps, this complexification is "roughly a 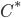algebra" according to Idel.  (I suspect, but don't recall offhand, that it is a direct sum of full matrix 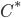algebras, i.e. isomorphic to a quantum system composed of several "superselection sectors" (the full matrix algebras in the sum), but as in the Euclidean case, not necessarily a 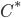-subalgebra of the ambient matrix algebra.)

I find this a remarkable result because I'm interested in places where Euclidean Jordan algebras appear in nature, or in mathematics.  One reason for this is that the finite-dimensional ones are in one-to-one correspondence with homogeneous, self-dual cones; perhaps I'll discuss this beautiful fact another time.  Alex Wilce, Phillip Gaebeler and I related the property of homogeneity to "steering" (which Schrödinger considered a fundamental weirdness of the newly developed quantum theory) in this paper.  I don't think I've blogged about this before, but Matthew Graydon, Alex Wilce, and I have developed ways of constructing composite systems of the general probabilistic systems based on reversible Jordan algebras, along with some results that I interpret as no-go theorems for such composites when one of the factors is not universally reversible.  The composites are still based on Jordan algebras, but are necessarily (if we wish them to still be Jordan-algebraic) not locally tomographic unless both systems are quantum.  Perhaps I'll post more on this later, too.  For now I just wanted to describe this cool result of Martin Idel's that I'm happy to have learned about today from Kasia.