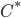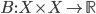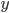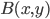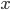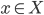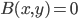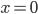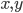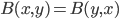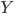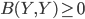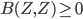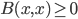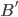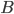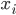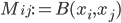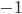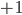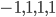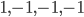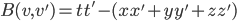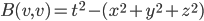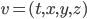Category Archives: General Probabilistic Theories

Strongly Symmetric Spectral Convex Sets are Jordan Algebra State Spaces

Posted on by

The title of this post is also the title of my most recent paper on the arXiv, from 2019, with Joachim Hilgert of the University of Paderborn. The published version is titled Spectral Properties of Convex Bodies, Journal of Lie Theory 30 (2020) 315-355.

Here's a preprint version of the J Lie Theory article:

BarnumHilgertSpectralPropertiesOfConvexBodiesPreprintVersion2Download

Compared to the arXiv version, the J Lie Theory version (and the above-linked preprint) has less detail about the background results by other authors (mainly Jiri Dadok's theory of polar representations of compact Lie groups, and the Madden-Robertson theory of regular convex bodies) which we use, and a bit more detail in the proof of our main result. It also has a more extensive discussion of infinite-dimensional Jordan algebraic systems, in the context of discussion of ways in which the Jordan algebraic systems can be narrowed down to the complex quantum ones. I like the title of the arXiv version better, since it states the main result of the paper, but Joachim was scheduled to give a talk at the celebration of Jimmie Lawson's 75th birthday in 2018, while we were writing up the main result, so he gave a talk on our work titled Spectral Properties…, and we decided to publish the paper in the proceedings, which are a special issue of J Lie Theory, so it ended up with the same title as the talk.

Here are slides from a talk on the result I gave to an audience of mathematicians and mathematical physicists:

MadridOperatorAlgebras2019

MadridOperatorAlgebras2019Download

Although the paper's main theorem is a result in pure mathematics, and, I think, interesting even purely from that point of view, it is also a result in the generalized probabilistic theories (GPT) framework for formulating physical theories from a very general point of view, which describes physical systems in terms of the probabilities of the various results of all possible ways of observing (we often say "measuring") those systems. The state in which a system has been prepared (whether by an experimenter or by some natural process) is taken to be defined by specifying these probabilities of measurement-results, and it is then very natural to take the set of all possible states in which a system can be prepared to be a compact convex set. Such sets are usually taken to live in some real affine space, for instance the three-dimensional one of familiar Euclidean geometry, which may be taken to host the qubit, whose state space is a solid ball, sometimes called the Bloch ball. In this framework, measurement outcomes are associated with affine functionals on the set taking real values---in fact, values between 0 and 1 --- probabilities, and measurements are associated with lists of such functionals, which add up to the unit functional---the constant functional taking the value 1 on all states of the system. (This ensures that whatever state of the system is prepared, the probabilities of outcomes of a measurement add up to 1.) This allows an extremely wide variety of convex sets as state spaces, most of which are neither the state spaces of quantum systems nor classical systems. An important part of the research program of those of us who spend some of our time working in the GPT framework is to characterize the state spaces of quantum systems by giving mathematically natural axioms, or axioms concerning the physical properties exhibited by, or the information-processing protocols we can implement using, such systems, such that all systems having these properties are quantum systems. To take just a few examples of the type of properties we might ask about: can we clone states of such systems? Do we have what Schroedinger called "steering" using entangled states of a pair of such systems? Can we define a notion of entropy in a way similar to the way we define the von Neumann entropy of a quantum system, and if so, are there thermodynamic protocols or processes similar to those possible with quantum systems, in which the entropy plays a similar role? Are there analogues of the spectral theorem for quantum states (density matrices), of the projection postulate of quantum theory, of the plethora of invertible transformations of the state space that are described, in the quantum case, by unitary operators? We often limit ourselves (as Joachim and I did in our paper) to finite-dimensional GPT systems to make the mathematics easier while still allowing most of the relevant conceptual points to become clear.

This paper with Joachim builds on work by me, Markus Mueller and Cozmin Ududec, who showed that three principles characterize irreducible finite-dimensional Jordan-algebraic systems (plus finite-dimensional classical state spaces). Since these systems were shown (by Jordan, von Neumann, and Wigner in the 1930s, shortly after Jordan defined the algebras named after him) to be just the finite-dimensional quantum systems over the real, complex, and quaternionic numbers, plus systems whose state space is a ball (of any finite dimension), plus three-dimensional quantum theory over the octonions (associated with the so-called exceptional Jordan algebra), this already gets us very close to a characterization of the usual complex quantum state space (of density matrices) and the associated measurement theory described by positive operators. The principles are (1) A generalized spectral decomposition: every state is a convex combination of perfectly distinguishable pure states, (2) Strong Symmetry: every set of perfectly distinguishable pure states may be taken to any other such set (of the same size) by a symmetry of the state space, and (3) that there is no irreducible three (or more) path interference. Joachim and I characterized the same class of systems using only (1) and (2). In order for you to understand these properties, I need to explain some terms used in them: pure states are defined as states that cannot be viewed as convex combinations of any other states---that is, there is no "noise" involved in their preparation---they are sometimes called "states of maximal information". The states in a given list of states are "perfectly distinguishable" from each other if, when we are guaranteed that the state of a system is one of those in the list, there is a single measurement that can tell us which state it is. The measurement that does the distinguishing may, of course, depend on which list it is. Indeed one can take it as a definition of classical system, at least in this finite-dimensional context, that there is a single measurement that is capable of distinguishing the states in any list of distinct pure states of the system.

If one wants to narrow things down further from the Jordan-algebraic systems to the complex quantum systems, there are known principles that will do it: for instance, energy observability (from the Barnum, Mueller, Ududec paper linked above, although it should be noted that it's closely related to concepts of Alfsen and Shultz ("dynamical correspondence") and of Connes ("orientation")): that the generators of continuous symmetries of the state space are also observables, and are conserved by the dynamics that they generate, a requirement very reminiscent of Noether's theorem on conserved generators of symmetries. Mathematically speaking, we formulate this as a requirement that the Lie algebra of the symmetry group of the state space embeds, injectively and linearly, into the space of observables (which we take to be the ambient real vector space spanned by the measurement outcomes) of the system, in such a way that the embedded image of a Lie algebra generator is conserved by the dynamics it generates. In the quantum case, this is just the fact that the Lie algebra su(n) of an n-dimensional quantum system's symmetry group is the real vector space of anti-Hermitian matrices, which embeds linearly (over the reals) and injectively into the Hermitian matrices (indeed, bijectively onto the traceless Hermitian matrices), which are of course the observables of a finite-dimensional quantum system. This embedding is so familiar to physicists that they usually just consider the generators of the symmetry group to be Hermitian matrices ("Hamiltonians"), and map them back to the antiHermitian generators by considering multiplication by i (that's the square root of -1) as part of the "generation" of unitary evolution. This is discussed in the arXiv version, but the Journal of Lie Theory version discusses it more extensively, and along the way indicates some results on infinite-dimensional Jordan algebraic systems since Alfsen and Shultz, and Connes, worked in frameworks allowing some infinite-dimensional systems. See also John Baez' excellent recent paper, Getting to the Bottom of Noether's Theorem. One can also narrow things down to complex quantum systems by requiring that systems compose in a "tomographically local" way, which means that there is a notion of composite system, made up of two distinct systems, such that all states of the composite system, even the entangled ones (a notion which makes sense in this general probabilistic context, not only in quantum theory), are determined by the probabilities they give to pairs of local meausurement outcomes (i.e. the way in which they correlate (or fail to correlate) these outcomes).

Anthony Aguirre is looking for postdoc at Santa Cruz in Physics of the Observer

Posted on by

Anthony Aguirre points out that UC Santa Cruz is advertising for postdocs in the "Physics of the Observer" program; and although review of applications began in December with a Dec. 15 deadline "for earliest consideration", if you apply fast you will still be considered.  He explicitly states they are looking for strong applicants from the quantum foundations community, among other things.

My take on this: The interaction of quantum and spacetime/gravitational physics is an area of great interest these days, and people doing rigorous work in quantum foundations, quantum information, general probabilistic theories have much to contribute.  It's natural to think about links with cosmology in this context.  I think this is a great opportunity, foundations postdocs and students, and Anthony and Max are good people to be connected with, very proactive in seeking out sources of funding for cutting-edge research and very supportive of interdisciplinary interaction.  The California coast around Santa Cruz is beautiful, SC is a nice funky town on the ocean, and you're within striking distance of the academic and venture capital powerhouses of the Bay Area.  So do it!

Martin Idel: the fixed-point sets of positive trace-preserving maps on quantum systems are Jordan algebras!

Posted on by

Kasia Macieszczak is visiting the ITP at Leibniz Universität Hannover (where I arrived last month, and where I'll be based for the next 7 months or so), and gave a talk on metastable manifolds of states in open quantum systems.  She told me about a remarkable result in the Master's thesis of Martin Idel at Munich: the fixed point set of any trace-preserving, positive (not necessarily completely positive) map on the space of Hermitian operators of a finite-dimensional quantum system, is a Euclidean Jordan algebra.  It's not necessarily a Jordan subalgebra of the usual Jordan algebra associated with the quantum system (whose Jordan product is the antisymmetrized matrix multiplication, ).  We use the usual characterization of the projector onto the fixed-point space of a linear map :  .  The maximum-rank fixed point is (where is the identity matrix), which we'll call , and the Jordan product on the fixed-point space is the original one "twisted" to have as its unit:  for fixed-points, this Jordan product, which I'll denote by , is:

which we could also write in terms of the original Jordan product as , where is the map defined by .

Idel's result, Theorem 6.1 in his thesis, is stated in terms of the map on all complex matrices, not just the  Hermitian ones; the fixed-point space is then the complexification of the Euclidean Jordan algebra.  In the case of completely positive maps, this complexification is "roughly a algebra" according to Idel.  (I suspect, but don't recall offhand, that it is a direct sum of full matrix algebras, i.e. isomorphic to a quantum system composed of several "superselection sectors" (the full matrix algebras in the sum), but as in the Euclidean case, not necessarily a -subalgebra of the ambient matrix algebra.)

I find this a remarkable result because I'm interested in places where Euclidean Jordan algebras appear in nature, or in mathematics.  One reason for this is that the finite-dimensional ones are in one-to-one correspondence with homogeneous, self-dual cones; perhaps I'll discuss this beautiful fact another time.  Alex Wilce, Phillip Gaebeler and I related the property of homogeneity to "steering" (which Schrödinger considered a fundamental weirdness of the newly developed quantum theory) in this paper.  I don't think I've blogged about this before, but Matthew Graydon, Alex Wilce, and I have developed ways of constructing composite systems of the general probabilistic systems based on reversible Jordan algebras, along with some results that I interpret as no-go theorems for such composites when one of the factors is not universally reversible.  The composites are still based on Jordan algebras, but are necessarily (if we wish them to still be Jordan-algebraic) not locally tomographic unless both systems are quantum.  Perhaps I'll post more on this later, too.  For now I just wanted to describe this cool result of Martin Idel's that I'm happy to have learned about today from Kasia.

ITFP, Perimeter: selective guide to talks. #1: Brukner on quantum theory with indefinite causal order

Posted on by

Excellent conference the week before last at Perimeter Institute: Information Theoretic Foundations for Physics.  The talks are online; herewith a selection of some of my favorites, heavily biased towards ideas new and particularly interesting to me (so some excellent ones that might be of more interest to you may be left off the list!).  Some of what would have been possibly of most interest and most novel to me happened on Weds., when the topic was spacetime physics and information, and I had to skip the day to work on a grant proposal.  I'll have to watch those online sometime.  This was going to be one post with thumbnail sketches/reviews of each talk, but as usual I can't help running on, so it may be one post per talk.

All talks available here, so you can pick and choose. Here's #1 (order is roughly temporal, not any kind of ranking...):

Caslav Brukner kicked off with some interesting work on physical theories in with indefinite causal structure.  Normally in formulating theories in an "operational" setting (in which we care primarily about the probabilities of physical processes that occur as part of a complete compatible set of possible processes) we assume a definite causal (partial) ordering, so that one process may happen "before" or "after" another, or "neither before nor after".  The formulation is "operational" in that an experimenter or other agent may decide upon, or at least influence, which set of processes, out of possible compatible sets, the actual process will be drawn, and then nature decides (but with certain probabilities for each possible process, that form part of our theory), which one actually happens.  So for instance, the experimenter decides to perform a Stern-Gerlach experiment with a particular orientation X of the magnets; then the possible processes are, roughly, "the atom was deflected in the X direction by an angle theta," for various angles theta.  Choose a different orientation, Y, for your apparatus, you choose a different set of possible compatible processes.  ("The atom was deflected in the Y direction by an angle theta.")  Then we assume that if one set of compatible processes happens after another, an agent's choice of which complete set of processes is realized later, can't influence the probabilities of processes occuring in an earlier set.  "No signalling from the future", I like to call this; in formalized operational theories it is sometimes called the "Pavia causality axiom".   Signaling from the past to the future is fine, of course.  If two complete  sets of processes are incomparable with respect to causal order ("spacelike-separated"), the no-signalling constraint operates both ways:  neither Alice's choice of which compatible set is realized, nor Bob's, can influence the probabilities of processes occuring at the other agent's site.   (If it could, that would allow nearly-instantaneous signaling between spatially separated sites---a highly implausible phenomenon only possible in preposterous theories such as the Bohmian version of quantum theory with "quantum disequilibrium", and Newtonian gravity. ) Anyway, Brukner looks at theories that are close to quantum, but in which this assumption doesn't necessarily apply: the probabilities exhibit "indeterminate causal structure".  Since the theories are close to quantum, they can be interpreted as allowing "superpositions of different causal structures", which is just the sort of thing you might think you'd run into in, say, theories combining features of quantum physics with features of general relativistic spacetime physics.  As Caslav points out, since in general relativity the causal structure is influenced by the distribution of mass and energy, you might hope to realize such indefinite causal structure by creating a quantum superposition of states in which a mass is in one place, versus being in another.  (There are people who think that at some point---some combinations of spatial scales (separation of the areas in which the mass is located) and mass scales (amount of mass to be separated in "coherent" superposition)) the possibility of such superpositions breaks down.  Experimentalists at Vienna (where Caslav---a theorist, but one who likes to work with experimenters to suggest experiments---is on the faculty) have created what are probably the most significant such superpositions.)

Situations with a superposition of causal orders seem to be exhibit some computational advantages over standard causally-ordered quantum computation, like being able to tell in fewer queries (one?) whether a pair of unitaries commutes or anticommutes.  Not sure whose result that was (Giulio Chiribella and others?), but Caslav presents some more recent results on query complexity in this model, extending the initial results.  I am generally wary about results on computation in theories with causal anomalies.  The stuff on query complexity with closed timelike curves, e.g. by Dave Bacon and by  Scott Aaronson and John Watrous has seemed uncompelling---not the correctness of the mathematical results, but rather the physical relevance of the definition of computation---to me for reasons similar to those given by Bennett, Leung, Smith and Smolin.  But I tend to suspect that Caslav and the others who have done these query results, use a more physically compelling framework because they are well versed in the convex operational or "general probabilistic theories" framework which aims to make the probabilistic behavior of processes consistent under convex combination ("mixture", i.e. roughly speaking letting somebody flip coins to decide which input to present your device with).  Inconsistency with respect to such mixing is part of the Bennett/Leung/Smolin/Smith objection to the CTC complexity classes as originally defined.

[Update:  This article at Physics.org quotes an interview with Scott Aaronson responding to the Bennett et. al. objections.  Reasonably enough, he doesn't think the question of what a physically relevant definition of CTC computing is has been settled.  When I try to think about this issue sometimes I wonder if the thorny philosophical question of whether we court inconsistency by trying to combine intervention ("free choice of inputs") in a physical theory is rearing its head.  As often with posts here, I'm reminding myself to revisit the issue at some point... and think harder.]

How does one prove that domains of positivity of symmetric nondegenerate bilinear forms are self-dual cones?

Posted on by

On mathoverflow, I've asked how one proves that domains of positivity of symmetric nondegenerate bilinear forms on real vector spaces are self-dual cones.  A bilinear form on a real vector space is just a map that is linear in each argument.  (In other words, if you fix , the function that takes to is linear, and similarly if you fix the other argument.)  It's called nondegenerate if the only such that for all , is .  And, of course, it's symmetric if for all , .

A closed domain of positivity of such a form is a maximal set such that .  Maximal means maximal in the ordering of sets by containment, i.e. is not contained in any other set satisfying .  This notion was introduced, or at least used, by Max Koecher in the late 1950s, in work that led to the celebrated result, published in 1958 in "The Geodesics of Domains of Positivity"  (well, actually, "Die Geodatische von Positivitatsbereichen" (Mathematische Annalen 135 (1958), pp. 192--202)), that homogeneous self-dual cones in finite dimension are precisely the cones of squares in finite-dimensional formally real (aka Euclidean) Jordan algebras.  Indeed, probably the very interpretation of the main result of that paper as concerning homogeneous self-dual cones relies on the identification of domains of positivity with self-dual cones that I'm looking for a proof of.

If the form were positive semidefinite, i.e. for all (which implies symmetry) then a domain of positivity for would clearly  be a self-dual cone.  This is practically the definition of a self-dual cone.  The dual of a cone in a real inner product space is the set of all vectors whose inner product with everything in the cone is nonnegative---and the definition of an inner product on a real vector space is that it's a nondegenerate positive semidefinite bilinear form.  A self-dual cone is one that's equal to its dual cone.

For our definition of domain of positivity, the form was required only to be symmetric, not necessarily also positive semidefinite.  Nevertheless, according to things I've read, its domains of positivity are self-dual cones.   These domains are not necessarily unique, of course, although they are maximal, i.e. no one of them contains another).  Although I have a vague recollection of having seen a proof that they are self-dual, I haven't been able to find the paper or come up with a proof.

It's easy to prove that such a domain is a pointed, convex, closed cone.  A natural way to prove that it is a self-dual cone would be to exhibit a positive semidefinite form , depending on and possibly also on , such that is a domain of positivity of .   An idea for how to do this involves the fact that such a form can be diagonalized: we can find a basis for the vector space such that the matrix with elements is diagonal, with diagonal elements .  The number of signs on the diagonal is the signature of the form.  A natural candidate for is the Euclidean inner product in the basis (i.e are the components of in this basis).  That is, we just change the 's to 's in the diagonal form of .

Nondegenerate symmetric bilinear forms are interesting for a variety of reasons.  One of them is that they are closely related to the metric structure on a pseudo-Riemannian manifold.  Something like the following is true: you specify such a form at each point of the manifold, in such a way that the forms at the various points are nicely related to each other, and you've specified the geometric structure of a pseudo-Riemannian manifold.  (One restriction here, I believe, is that the signature of the forms has to be the same everywhere; the forms also need to vary somewhat smoothly, in a manner I should look up and summarize, but not now.)  For example, in the general relativistic description of spacetime, the spacetime manifold has signature .  Or ; people use different conventions.  I'm attracted to , because the odd-one-out corresponds in relativity theory to time, and this way, the forward and backward light cones are the (only!) domains of positivity for the form.  I.e. the form is ; we have (here , etc...).  Interestingly, with the other choice of signature, the domains of positivity consist of spacelike vectors, and there is a continuum of them.  To get a picture of what's going on, consider one time and two space dimensions, with signature .  You can visualize this in , with the vertical axis as time (associated with the diagonal element of the form) and the horizontal planes for constant time as a spacelike plane.  If you rotate the 45 degree line between and say the axis, around the axis, you get the boundary of a double cone, the forward and backward light cones.  But similar cones pointing along any ray in the plane are clearly domains of positivity for the form.  I suspect lots of other cones---basically, any self-dual cone you can fit into the "conic doughnut" that is the closed complement of the double light-cone, i.e. into the spacelike (and null) vectors, are also domains of positivity for this form.

My main reason for interest in the problem isn't pseudo-Riemannian geometry, however.  More on the main reason later.  (It has to do with the Koecher result cited above).

If you found this problem first on mathoverflow, and you have the answer, please post your answer there, and link to it here if you feel like it; if you encountered it first here, please post the answer here indicating you encountered the problem here, and it would be nice if you'd also post it on mathoverflow indicating you found it on my blog.  We can have a little race between we happy few who read this blog, and the overflowing mathematicians.  I know who I'm betting on---your mission, readers, should you choose to accept it, and should any of you actually exist, is to prove me wrong!

(Thanks to Will Jagy, of MSRI, for noticing that I defined nondegeneracy wrong here at first: as requiring that the only for which is . This wrong definition, corrected above, of course says that the form has no nontrivial "isotropic" or "null" vectors (ones for which ). And we certainly don't want to assume that! Sorry about the slip-up, which I dont think affected anything else in the post.)

Gross, Mueller, Colbeck, and Dahlsten: "All reversible dynamics in maximally non-local theories are trivial"

Posted on by

David Gross, Markus Mueller, Roger Colbeck, and Oscar Dahlsten have considered the "maximal non-signaling tensor product" of "boxlets", and shown that the reversible dynamics of this state space consists just of permutations of the systems (the boxlets) followed by reversible local transformations (i.e., ones on the individual boxlets).

What the heck does that mean, you ask?  Well, "boxlets" were introduced in several contexts.  In the "operational quantum logic" literature they're sometimes called "semiclassical test spaces".  In quantum foundations and informations, they were introduced as a generalization of a notion of Popescu and Rohrlich, who introduced the two-measurement, two-outcome-per-measurement boxlet in order to describe correlations between measurement results on distinct systems that can be stronger than quantum correlations, but still don't allow someone ("Alice") in possession of one of the systems to signal to the other ("Bob") just by making measurements on her system.

A "boxlet" is a system on which there are M distinct alternative measurements one can make, each with K outcomes.  (More complex versions allow different measurements to have different numbers of outcomes.)  The allowable states of a boxlet are given by specifying M probability distributions, each one over K alternatives:  for each measurement, the probabilities of each of its K outcomes.  All possible lists of M such distributions are allowed; this is a convex, compact subset of an MK dimensional vector space (one dimension for each probability).  The M normalization constraints mean that this set lies in an MK-M (i.e., M(K-1)) dimensional affine subspace  (higher dimensional generalization of the line, plane, etc... of high-school geometry).  The possible states of a pair of such systems are given by the "maximal tensor product" of a pair of these compact convex state spaces.  The technical definition of maximal tensor product of state spaces can be found here.  Another way of defining this is that it's the state space of the  Foulis-Randall tensor product  of the "test spaces" (definitions reviewed in Sections II and IV of this paper) describing each of the boxlets.  A test space is just a collection of subsets of some set; the elements of the set interpreted as measurement outcomes, and the subsets, called "tests", as measurements.  The semiclassical test space of a boxlet like the ones I described above just consists of a set of MK elements, partitioned into M sets of K elements.  A state on a (finite, like the ones in question) test space is a function from the set to the real numbers between zero and 1, i.e. to probabilities, such that for each test, the probabilities of the elements of the test add up to one.  The Foulis-Randall tensor product of two test spaces just takes their Cartesian product, and allows any probability assignments such that the "marginal states" obtained by fixing a measurement on one side and marginalizing all the joint distributions of this fixed measurement with measurements on the other side, is independent of which measurement is marginalized over.  That is, Alice can't signal to Bob (by affecting the probabilities of the outcomes of one or more of his measurements) just by her choice of measurement.

Now, a transformation of the state space is an affine map from the state space to itself (i.e. one that preserves convex combination, which seems only reasonable), and a reversible one is one that has an inverse that is also an affine map of the state space.  So what GMCD are saying is that, if you combine boxlets this way, there are no very interesting reversible dynamics:  just combinations of local reversible dynamics on the individual boxlets, and permuting the boxes amongst themselves.

An interesting question is, can one extend this result to maximal tensor products of *arbitrary* systems with convex state space (locally equipped, let's say, with the maximal set of possible effects)?

See the comments on the Information Causality thread at Dave Bacon's blog for a bit more discussion (and related interesting matters).