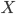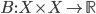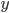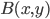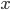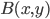On mathoverflow, I've asked how one proves that domains of positivity of symmetric nondegenerate bilinear forms on real vector spaces are self-dual cones.  A bilinear form on a real vector space is just a map that is linear in each argument.  (In other words, if you fix , the function that takes to is linear, and similarly if you fix the other argument.)  It's called nondegenerate if the only 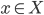such that 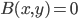for all 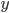, is 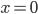.  And, of course, it's symmetric if for all , .

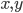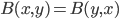A closed domain of positivity of such a form is a maximal set 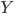such that 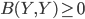.  Maximal means maximal in the ordering of sets by containment, i.e. 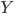is not contained in any other set 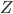satisfying 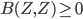.  This notion was introduced, or at least used, by Max Koecher in the late 1950s, in work that led to the celebrated result, published in 1958 in "The Geodesics of Domains of Positivity"  (well, actually, "Die Geodatische von Positivitatsbereichen" (Mathematische Annalen 135 (1958), pp. 192--202)), that homogeneous self-dual cones in finite dimension are precisely the cones of squares in finite-dimensional formally real (aka Euclidean) Jordan algebras.  Indeed, probably the very interpretation of the main result of that paper as concerning homogeneous self-dual cones relies on the identification of domains of positivity with self-dual cones that I'm looking for a proof of.

If the form were positive semidefinite, i.e. 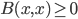for all 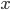(which implies symmetry) then a domain of positivity for would clearly  be a self-dual cone.  This is practically the definition of a self-dual cone.  The dual of a cone in a real inner product space is the set of all vectors 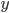whose inner product with everything in the cone is nonnegative---and the definition of an inner product on a real vector space is that it's a nondegenerate positive semidefinite bilinear form.  A self-dual cone is one that's equal to its dual cone.

For our definition of domain of positivity, the form was required only to be symmetric, not necessarily also positive semidefinite.  Nevertheless, according to things I've read, its domains of positivity are self-dual cones.   These domains are not necessarily unique, of course, although they are maximal, i.e. no one of them contains another).  Although I have a vague recollection of having seen a proof that they are self-dual, I haven't been able to find the paper or come up with a proof.

It's easy to prove that such a domain is a pointed, convex, closed cone.  A natural way to prove that it is a self-dual cone would be to exhibit a positive semidefinite form 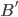, depending on 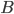and possibly also on 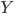, such that 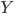is a domain of positivity of 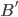.   An idea for how to do this involves the fact that such a form can be diagonalized: we can find a basis 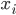for the vector space such that the matrix with elements 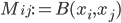is diagonal, with diagonal elements 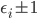.  The number of signs on the diagonal is the signature of the form.  A natural candidate for 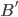is the Euclidean inner product 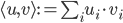in the basis 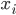(i.e 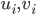are the components of 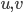in this basis).  That is, we just change the 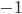's to 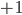's in the diagonal form of .

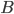Nondegenerate symmetric bilinear forms are interesting for a variety of reasons.  One of them is that they are closely related to the metric structure on a pseudo-Riemannian manifold.  Something like the following is true: you specify such a form at each point of the manifold, in such a way that the forms at the various points are nicely related to each other, and you've specified the geometric structure of a pseudo-Riemannian manifold.  (One restriction here, I believe, is that the signature of the forms has to be the same everywhere; the forms also need to vary somewhat smoothly, in a manner I should look up and summarize, but not now.)  For example, in the general relativistic description of spacetime, the spacetime manifold has signature 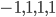.  Or 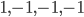; people use different conventions.  I'm attracted to 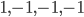, because the odd-one-out corresponds in relativity theory to time, and this way, the forward and backward light cones are the (only!) domains of positivity for the form.  I.e. the form is 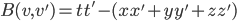; we hav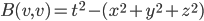e (here 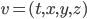, etc...).  Interestingly, with the other choice of signature, the domains of positivity consist of spacelike vectors, and there is a continuum of them.  To get a picture of what's going on, consider one time and two space dimensions, with signature 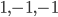.  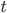You can visualize this in , with the vertical axis as time (associated with the 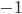diagonal element of the form) and the horizontal 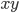planes for constant time 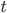as a spacelike plane.  If you rotate the 45 degree line between 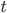and say the 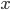axis, around the 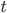axis, you get the boundary of a double cone, the forward and backward light cones.  But similar cones pointing along any ray in the 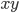plane are clearly domains of positivity for the form.  I suspect lots of other cones---basically, any self-dual cone you can fit into the "conic doughnut" that is the closed complement of the double light-cone, i.e. into the spacelike (and null) vectors, are also domains of positivity for this form.

My main reason for interest in the problem isn't pseudo-Riemannian geometry, however.  More on the main reason later.  (It has to do with the Koecher result cited above).

If you found this problem first on mathoverflow, and you have the answer, please post your answer there, and link to it here if you feel like it; if you encountered it first here, please post the answer here indicating you encountered the problem here, and it would be nice if you'd also post it on mathoverflow indicating you found it on my blog.  We can have a little race between we happy few who read this blog, and the overflowing mathematicians.  I know who I'm betting on---your mission, readers, should you choose to accept it, and should any of you actually exist, is to prove me wrong!

(Thanks to Will Jagy, of MSRI, for noticing that I defined nondegeneracy wrong here at first: as requiring that the only 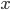for which 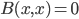is 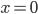. This wrong definition, corrected above, of course says that the form has no nontrivial "isotropic" or "null" vectors (ones for which 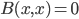). And we certainly don't want to assume that! Sorry about the slip-up, which I dont think affected anything else in the post.)