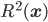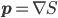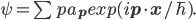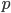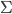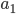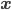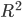Category Archives: Philosophy

Deutsch, Popper, Gelman and Shalizi, with a side of Mayo, on Bayesian ideas, models and fallibilism in the philosophy of science and in statistics (I)

Posted on by

A few years back, when I reviewed David Deutsch's The Beginning of Infinity for Physics Today (see also my short note on the review at this blog), I ended up spending a fair amount of time revisiting an area of perennial interest to me: the philosophy of science, and the status of Popper's falsificationist and anti-inductive view of scientific reasoning. I tend to like the view that one should think of scientific reasoning in terms of coherently updating subjective probabilities, which might be thought of as Bayesian in a broad sense. (Broad because it might be more aligned with Richard Jeffrey's point of view, in which any aspect of one's probabilities might be adjusted in light of experience, rather than a more traditional view on which belief change is always and only via conditioning the probabilities of various hypotheses on newly acquired data, with one's subjective probabilities of data given the hypotheses never adjusting.) I thought Deutsch didn't give an adequate treatment of this broadly Bayesian attitude toward scientific reasoning, and wrote:

Less appealing is Deutsch and Popper’s denial of the validity of inductive reasoning; if this involves a denial that evidence can increase the probability of general statements such as scientific laws, it is deeply problematic. To appreciate the nature and proper role of induction, one should also read such Bayesian accounts as Richard Jeffrey’s (Cambridge University Press, 2004) and John Earman’s (MIT Press, 1992).

Deutsch and Popper also oppose instrumentalism and physical reductionism but strongly embrace fallibilism. An instrumentalist believes that particular statements or entities are not literally true or real, but primarily useful for deriving predictions about other matters. A reductionist believes that they have explanations couched in the terms of some other subject area, often physics. Fallibilism is the view that our best theories and explanations are or may well be false. Indeed many of the best have already proved not to be strictly true. How then does science progress? Our theories approximate truth, and science replaces falsified theories with ones closer to the truth. As Deutsch puts it, we “advance from misconception to ever better misconception.” How that works is far from settled. This seems to make premature Deutsch’s apparent dismissal of any role for instrumentalist ideas, and his neglect of pragmatist ones, according to which meaning and truth have largely to do with how statements are used and whether they are useful.

Thanks to Brad DeLong I have been reading a very interesting paper from a few years back by Andrew Gelman and Cosma Shalizi, "Philosophy and the practice of Bayesian statistics" that critiques the Bayesian perspective on the philosophy of science from a broadly Popperian---they say "hypothetico-deductive"---point of view, that embraces (as did Popper in his later years) fallibilism (in the sense of the quote from my review above).  They are particularly concerned to point out that the increasing use of Bayesian methods in statistical analysis should not necessarily be interpreted as supporting a Bayesian viewpoint on the acquisition of scientific knowledge more generally.  That point is well taken; indeed I take it to be similar to my point in this post that the use of classical methods in statistical analysis need not be interpreted as supporting a non-Bayesian viewpoint on the acquisition of knowledge.  From this point of view, statistical analysis, whether formally Bayesian or "classical" is an input to further processes of scientific reasoning; the fact that Bayesian or classical methods may be useful at some stage of statistical analysis of the results of some study or experiment does not imply that all evaluation of the issues being investigated must be done by the same methods.  While I was most concerned to point out that use of classical methods in data analysis does not invalidate a Bayesian (in the broad sense) point of view toward how the results of that analysis should be integrated with the rest of our knowledge, Gelman and Shalizi's point is the mirror image of this.  Neither of these points, of course, is decisive for the "philosophy of science" question of how that broader integration of new experience with knowledge should proceed.

Although it is primarily concerned to argue against construing the use of  Bayesian methods in data analysis as supporting a Bayesian view of scientific methods more generally, Gelman and Shalizi's paper does also contain some argument against Bayesian, and more broadly "inductive", accounts of scientific method, and in favor of a broadly Popperian, or what they call "hypothetico-deductive" view.  (Note that they distinguish this from the "hypothetico-deductive" account of scientific method which they associate with, for instance, Carl Hempel and others, mostly in the 1950s.)

To some extent, I think this argument may be reaching a point that is often reached when smart people, indeed smart communities of people,  discuss, over many years, fundamental issues like this on which they start out with strong differences of opinion:  positions become more nuanced on each side, and effectively closer, but each side wants to keep the labels they started with, perhaps in part as a way of wanting to point to the valid or partially valid insights that have come from "their" side of the argument (even if they have come from the other side as well in somewhat different terms), and perhaps also as a way of wanting to avoid admitting having been wrong in "fundamental" ways.  For example, one sees insights similar to those in the work of Richard Jeffrey and others from a "broadly Bayesian" perspective, about how belief change isn't always via conditionalization using fixed likelihoods, also arising in the work of the "hypothetico-deductive" camp, where they are used against the simpler "all-conditionalization-all-the-time" Bayesianism.  Similarly, probably Popperian ideas played a role in converting some  "relatively crude" inductivists to more sophisticated Bayesian or Jefferian approach.  (Nelson Goodman's "Fact, Fiction, and Forecast", with its celebrated "paradox of the grue emeralds", probably played this role a generation or two later.)  Roughly speaking, the "corroboration" of hypotheses of which Popper speaks, involves not just piling up observations compatible with the hypothesis (a caricature of "inductive support") but rather the passage of stringent tests. In the straight "falsification"  view of Popper, these are stringent because there is a possibility they will generate results inconsistent with the hypothesis, thereby "falsifying" it; on the view which takes it as pointing toward a more Bayesian view of things (I believe I once read something by I.J.Good in which he said that this was the main thing to be gotten from Popper), this might be relaxed to the statement that there are outcomes that are very unlikely if the hypothesis is true, thereby having the potential, at least, of leading to a drastic lowering of the posterior probability of the hypothesis (perhaps we can think of this as a softer version of falsification) if observed.  The posterior probability given that such an outcome is observed of course does not depend only on the prior probability of the hypothesis and the probability of the data conditional on the hypothesis---it also depends on many other probabilities.  So, for instance, one might also want such a test to have the property that "it would be difficult (rather than easy) to get an accordance between data x and H (as strong as the one obtained) if H were false (or specifiably flawed)".  The quote is from this post on Popper's "Conjectures and Refutations" by philosopher of science D. G. Mayo, who characterizes it as part of "a modification of Popper".  ("The one obtained" refers to an outcome in which the hypothesis is considered to pass the test.)  I view the conjunction of these two aspects of a test of a hypothesis or theory as rather Bayesian in spirit.  (I do not mean to attribute this view to Mayo.)
I'll focus later---most likely in a follow-up post---on Gelman and Shalizi's direct arguments against inductivism and more broadly Bayesian approaches to scientific methodology and the philosophy of science.  First I want to focus on a point that bears on these questions but arises in their discussion of Bayesian data analysis.  It is that in actual Bayesian statistical data analysis "the prior distribution is one of the assumptions of the model and does not need to represent the statistician's personal degree of belief in alternative parameter values".  They go on to say "the prior is connected to the data, so is potentially testable".  It is presumably just this sort of testing that Matt Leifer was referring to when he wrote (commenting on my earlier blog entry on Bayesian methods in statistics)

"What I often hear from statisticians these days is that it is good to use Bayesian methods, but classical methods provide a means to check the veracity of a proposed Bayesian method. I do not quite understand what they mean by this, but I think they are talking at a much more practical level than the abstract subjective vs. frequentist debate in the foundations of probability, which obviously would not countenance such a thing.

The point Gelman and Shalizi are making is that the Bayesian prior being used for data analysis may not capture "the truth", or more loosely, since they are taking into account the strong possibility that no model under consideration is literally true, that it may not adequately capture those aspects of the truth one is interested in---for example, may not be good at predicting things one is interested in. Hence one wants to do some kind of test of whether or not the model is acceptable. This can be based on using the Bayesian posterior distribution as a model to be tested further, typically with classical tests such as "pure significance tests".
As Matthew's comment above might suggest, those of us of more Bayesian tendencies, who might agree that the particular family of priors---and potential posteriors---being used in data analysis (qua "parameter fitting" where perhaps we think of the prior distribution as the (higher-level) "parameter" being fit) might well not "contain the truth", might be able to take these tests of the model, even if done using some classical statistic, as fodder for further, if perhaps less formal, Bayesian/Jeffreysian reasoning about what hypotheses are likely to do a good job of predicting what is of interest.

One of the most interesting things about Gelman and Shalizi's paper is that they are thinking about how to deal with "fallibilism" (Popper's term?), in particular, inference about hypotheses that are literally false but useful. This is very much in line with recent discussion at various blogs of the importance of models in economics, where it is clear that the models are so oversimplified as to be literally false, but nonetheless they may prove predictively useful.  (The situation is complicated, however, by the fact that the link to prediction may also be relatively loose in economics; but presumably it is intended to be there somehow.)  It is not very clear how Popperian "falsificationism" is supposed to adapt to the fact that most of the hypotheses that are up for falsification are already known to be false. Probably I should go back and see what Popper had to say on that score, later in his career when he had embraced fallibilism. (I do recall that he tried introducing a notion of "verisimilitude", i.e. some kind of closeness to the truth, and that the consensus seems to have been---as Gelman and Shalizi point out in a footnote---that this wasn't very successful.)  It seems to that a Bayesian might want to say one is reasoning about the probability of statements like "the model is a good predictor of X in circumstances Y", " the model does a good job capturing how W relates to Z" , and so forth. It is perhaps statements like these that are really being tested when one does the " pure significance tests" advocated by Gelman and Shalizi when they write things like "In designing a good test for model checking, we are interested in finding particular errors which, if present, would mess up particular inferences, and devise a test statistic which is sensitive to this sort of mis-specification."

As I said above, I hope to take up Gelman and Shalizi's more direct arguments (in the cited paper) against "inductivism" (some of which I may agree with) and Bayesianism sensu lato as scientific methodology in a later post. I do think their point that the increasing use of Bayesian analysis in actual statistical practice, such as estimation of models by calculating a posterior distribution over model parameters beginning with some prior, via formal Bayesian conditioning, does not necessarily tell in favor of a Bayesian account of scientific reasoning generally, is important. In fact this point is important for those who do hold such a loosely Bayesian view of scientific reasoning:  most of us do not wish to get stuck with interpreting such priors as the full prior input to the scientific reasoning process.  There is always implicit the possibility that such a definite specification is wrong, or, when it is already known to be wrong but thought to be potentially useful for some purposes nonetheless, "too wrong to be useful for those purposes".

A thought on resistance to Bayesian statistics

Posted on by

I'm not a statistician, and as a quantum theorist of a relatively abstract sort, I've done little actual data analysis.  But because of my abstract interests, the nature of probability and its use in making inferences from data are of great interest.  I have some relatively ill-informed thoughts on why the "classical statistics" community seems to have been quite resistant to "Bayesian statistics", at least for a while, that may be of interest, or at least worth logging for my own reference. Take this post in the original (?) spirit of the term "web log", rather than as a polished piece of the sort many blogs, functioning more in the spirit of online magazines, seem to aim at nowadays.

The main idea is this.  Suppose doing Bayesian statistics is thought of as actually adopting a prior which specifies, say, one's initial estimate of the probabilities of several hypotheses, and then, on the basis of the data, computing the posterior probability of the hypotheses.  In other words, what is usually called "Bayesian inference". That may be a poor way of presenting the results of an experiment, although it is a good way for individuals to reason about how the results of the experiment should affect their beliefs and decisions.  The problem is that different users of the experimental results, e.g. different readers of a published study, may have different priors.  What one would like is rather to present these users with a statistic, that is, some function of the data, much more succinct than simply publishing the data themselves, but just as useful, or almost as useful, in making the transition from prior probabilities to posterior probabilities, that is, of updating one's beliefs about the hypotheses of interest, to take into account the new data. Of course, for a compressed version of the data (a statistic) to be useful, it is probably necessary that the users share certain basic assumptions about the nature of the experiment.  These assumptions might involve the probabilities of various experimental outcomes, or sets of data, if various hypotheses are true (or if a parameter takes various values), i.e., the likelihood function;  they might also involve a restriction on the class of priors for which the statistic is likely to be useful.  These should be spelled out, and, if it is not obvious, how the statistic can be used in computing posterior probabilities should be spelled out as well.

It seems to me likely that many classical or "frequentist" statistics may be used in such a way; but, quite possibly, classical language, like saying that statistical inference leads to "acceptance" or "rejection" of hypotheses, tends to obscure this more desirable use of the statistic as a potential input to the computation of posterior probabilities.  In fact, I think people tend to have a natural tendency to want some notion of what the posterior probability of a hypothesis is; this is one source of the erroneous tendency, still sometimes found among the public, to confuse confidence levels with probabilities.  Sometimes an advocacy of classical statistical tests may go with an ideological resistance to the computation of posterior probabilities, but I suppose not always.  It also seems likely that in many cases, publishing actual Bayesian computations may be a good alternative to classical procedures, particularly if one is able to summarize in a formula what the data imply about posterior probabilities, for a broad enough range of priors that many or most users would find their prior beliefs adequately approximated by them.  But in any case, I think it is essential, in order to properly understand the meaning of reports of classical statistical tests, to understand how they can be used as inputs to Bayesian inference.  There may be other issues as well, e.g. that in some cases classical tests may make suboptimal use of the information available in the data.  In other words, they may not provide a sufficient statistic: a function of the data that contains all the information available in the data, about some random variable of interest (say, whether a particular hypothesis is true or not). Of course whether or not a statistic is sufficient will depend on how one models the situation.

Most of this is old hat, but it is worth keeping in mind, especially as a Bayesian trying to understand what is going on when "frequentist" statisticians get defensive about general Bayesian critiques of their methods.

Bohm on measurement in Bohmian quantum theory

Posted on by

Prompted, as described in the previous post, by Craig Callender's post on the uncertainty principle, I've gone back to David Bohm's original series of two papers "A suggested interpretation of the quantum theory in terms of "hidden" variables I" and "...II", published in Physical Review in 1952 (and reprinted in Wheeler and Zurek's classic collection "Quantum Theory and Measurement", Princeton University Press, 1983).  The Bohm papers and others appear to be downloadable here.

Question 1 of my previous post asked whether it is true that

"a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus."

It is fairly clear from Bohm's papers that the answer is "Yes". In section 5 of the second paper, he writes

"in the measurement of an "observable," Q, we cannot obtain enough information to provide a complete specification of the state of an electron, because we cannot infer the precisely defined values of the particle momentum and position, which are, for example, needed if we wish to make precise predictions about the future behavior of the electron. [...] the measurement of an "observable" is not really a measurement of any physical property belonging to the observed system alone. Instead, the value of an "observable" measures only an incompletely predictable and controllable potentiality belonging just as much to the measuring apparatus as to the observed system itself."

Since the first sentence quoted says we cannot infer precise values of "momentum and position", it is possible to interpret it as referring to an uncertainty-principle-like tradeoff of precision in measurement of one versus the other, rather than a statement that it is not possible to measure either precisely, but I think that would be a misreading, as the rest of the quote, which clearly concerns any single observable, indicates. Later in the section, he unambiguously gives the answer "Yes" to a mutation of my Question 1 which substitutes momentum for position. Indeed, most of the section is concerned with using momentum measurement as an example of the general principle that the measurements described by standard quantum theory, when interpreted in his formalism, do not measure pre-existing properties of the measured system.

Here's a bit of one of two explicit examples he gives of momentum measurement:

"...consider a stationary state of an atom, of zero angular momentum. [...] the -field for such a state is real, so that we obtain

Thus, the particle is at rest. Nevertheless, we see from (14) and (15) that if the momentum "observable" is measured, a large value of this "observable" may be obtained if the -field happens to have a large fourier coefficient, , for a high value of . The reason is that in the process of interaction with the measuring apparatus, the -field is altered in such a way that it can give the electron particle a correspondingly large momentum, thus transferring some of the potential energy of interaction of the particle with its -field into kinetic energy."

Note that the Bohmian theory involves writing the complex-valued wavefunction as , i.e. in terms of its (real) modulus and (real) phase . Expressing the Schrödinger equation in terms of these variables is in fact probably what suggested the interpretation, since one gets something resembling classical equations of motion, but with a term that looks like a potential, but depends on . Then one takes these classical-like equations of motion seriously, as governing the motions of actual particles that have definite positions and momenta. In order to stay in agreement with quantum theory concerning observed events such as the outcomes of measurements, m theory, one in addition keeps, from quantum theory, the assumption that the wavefunction evolves according to the Schrödinger equation. And one assumes that we don't know the particles' exact position but only that this is distributed with probability measure given (as quantum theory would predict for the outcome of a position measurement) by , and that the momentum is . That's why the real-valuedness of the wavefunction implies that momentum is zero: because the momentum, in Bohmian theory, is the gradient of the phase of the wavefunction.

For completeness we should reproduce Bohm's (15).

(15)

At least in the Wheeler and Zurek book, the equation has instead of as the subscript on , and instead of ; I consider these typos, and have corrected them. (Bohm's reference to (14), which is essentially the same as (15) seems to me to be redundant.)

The upshot is that

"the actual particle momentum existing before the measurement took place is quite different from the numerical value obtained for the momentum "observable,"which, in the usual interpretation, is called the "momentum." "

It would be nice to have this worked out for a position measurement example, as well. The nicest thing, from my point of view, would be an example trajectory, for a definite initial position, under a position-measurement interaction, leading to a final position different from the initial one. I doubt this would be too hard, although it is generally considered to be the case that solving the Bohmian equations of motion is difficult in the technical sense of complexity theory. I don't recall just how difficult, but more difficult than solving the Schrödinger equation, which is sometimes taken as an argument against the Bohmian interpretation: why should nature do all that work, only to reproduce, because of the constraints mentioned above---distribution of according to , ---observable consequences that can be more easily calculated using the Schrödinger equation?
I think I first heard of this complexity objection (which is of course something of a matter of taste in scientific theories, rather than a knockdown argument) from Daniel Gottesman, in a conversation at one of the Feynman Fests at the University of Maryland, although Antony Valentini (himself a Bohmian) has definitely stressed the ability of Bohmian mechanics to solve problems of high complexity, if one is allowed to violate the constraints that make it observationally indistinguishable from quantum theory. It is clear from rereading Bohm's 1952 papers that Bohm was excited about the physical possibility of going beyond these constraints, and thus beyond the limitations of standard quantum theory, if his theory was correct.

In fairness to Bohmianism, I should mention that in these papers Bohm suggests that the constraints that give standard quantum behavior may be an equilibrium, and in another paper he gives arguments in favor of this claim. Others have since taken up this line of argument and done more with it. I'm not familiar with the details. But the analogy with thermodynamics and statistical mechanics breaks down in at least one respect, that one can observe nonequilibrium phenomena, and processes of equilibration, with respect to standard thermodynamics, but nothing like this has so far been observed with respect to Bohmian quantum theory. (Of course that does not mean we shouldn't think harder, guided by Bohmian theory, about where such violations might be observed... I believe Valentini has suggested some possibilities in early-universe physics.)

A question about measurement in Bohmian quantum mechanics

Posted on by

I was disturbed by aspects of Craig Callender's post "Nothing to see here," on the uncertainty principle, in the New York Times' online philosophy blog "The Stone," and I'm pondering a response, which I hope to post here soon.  But in the process of pondering, some questions have arisen which I'd like to know the answers to.  Here are a couple:

Callender thinks it is important that quantum theory be formulated in a way that does not posit measurement as fundamental.  In particular he discusses the Bohmian variant of quantum theory (which I might prefer to describe as an alternative theory) as one of several possibilities for doing so.  In this theory, he claims,

Uncertainty still exists. The laws of motion of this theory imply that one can’t know everything, for example, that no perfectly accurate measurement of the particle’s velocity exists. This is still surprising and nonclassical, yes, but the limitation to our knowledge is only temporary. It’s perfectly compatible with the uncertainty principle as it functions in this theory that I measure position exactly and then later calculate the system’s velocity exactly.

While I've read Bohm's and Bell's papers on the subject, and some others, it's been a long time in most cases, and this theory is not something I consider very promising as physics even though it is important as an illustration of what can be done to recover quantum phenomena in a somewhat classical theory (and of the weird properties one can end up with when one tries to do so).  So I don't work with it routinely.  And so I'd like to ask anyone, preferably more expert than I am in technical aspects of the theory, though not necessarily a de Broglie-Bohm adherent, who can help me understand the above claims, in technical or non-technical terms, to chime in in the comments section.

I have a few specific questions.  It's my impression that in this theory, a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus.

Question 1:  Is that correct?

A little more discussion of Question 1.  On my understanding, what is claimed is, rather, something like: that if one has a probability distribution over particle positions and momenta and a "pilot wave" (quantum wave function) whose squared amplitude agrees with these distributions (is this required in both position and momentum space? I'm guessing so), then the probability (calculated using the distribution over initial positions and momenta, and the deterministic "laws of motion" by which these interact with the "pilot wave" and the apparatus) for the apparatus to end up showing position in a given range, is the same as the integral of the squared modulus of the wavefunction, in the position representation, over that range.  Prima facie, this could be achieved in ways other than having the measurement reading being perfectly correlated with the initial position on a given trajectory, and my guess is that in fact it is not achieved in that way in the theory.    If that were so it seems like the correlation should hold whatever the pilot wave is.  Now, perhaps that's not a problem, but it makes the pilot wave feel a bit superfluous to me, and I know that it's not, in this theory.  My sense is that what happens is more like:  whatever the initial position is, the pilot wave guides it to some---definite, of course---different final position, but when the initial distribution is given by the squared modulus of the pilot wave itself, then the distribution of final positions is given by the squared modulus of the (initial, I guess) pilot wave.

But if the answer to question 1 is "Yes", I have trouble understanding what Callender means by "I measure position exactly".  Also, regardless of the answer to Question 1, either there is a subtle distinction being made between measuring "perfectly accurately" and measuring "exactly" (in which case I'd like to know what the distinction is), or these sentences need to be reformulated more carefully.  Not trying to do a gotcha on Callender here, just trying to understand the claim, and de Broglie Bohm.

My second question relates to Callender's statement that:

It’s perfectly compatible with the uncertainty principle as it functions in this theory that I measure position exactly and then later calculate the system’s velocity exactly

Question 2: How does this way of ascertaining the system's velocity differ from the sort of "direct measurement" that is, presumably, subject to the uncertainty principle? I'm guessing that by the time one has enough information (possibly about further positions?) to calculate what the velocity was, one can't do with it the sorts of things that one could have done if one had known the position and velocity simultaneously.  But this depends greatly on what it would mean to "have known" the position and/or velocity, which --- especially if the answer to Question 1 was "Yes"--- seems a rather subtle matter.

So, physicists and other readers knowledgeable on these matters (if any such exist), your replies with explanations, or links to explanations, of these points would be greatly appreciated.  And even if you don't know the answers, but know de Broglie-Bohm well on a technical level... let's figure this out!  (My guess is that it's well known, and indeed that the answer to Question 1 in particular is among the most basic things one learns about this interpretation...)

Nagel's Mind and Cosmos, Objective Value, Delong and Blackburn

Posted on by

I have trouble understanding why critics of Thomas Nagel's Mind and Cosmos are coming down so hard on his belief that value statements---particularly ethical ones, can (some of them, at any rate) be objectively true or false.  I'll consider two examples here.  Brad DeLong's objection seems to me based primarily on his continued mistaken view that Nagel views his reason as infallible.  It's therefore not specific to the case of moral or other value judgments.  Simon Blackburn's objections are more interesting because they are more specific to value judgments, and better address Nagel's actual position.

Brad DeLong seems to think that Nagel's juxtaposition of reasoning in the form modification of a belief about the direction one is driving in, because of its inconsistency with newly acquired evidence, with reasoning like Nagel's "I oppose the abolition of the inheritance tax... because I recognize that the design of property rights should be sensitive not only to autonomy but also to fairness..." is self-evidently ridiculous.  Says Brad:

"I do wonder: Does Gene Callahan have any idea what he has committed himself to when he endorses Thomas Nagel's claim that Nagel has transcendent direct access to truths of objective reality? I think not:

Thomas Nagel: [...my (HB's) ellipsis here, in place of a typo by Brad that repeated part of his own introduction, quoted above, to this quote...] I decide, when the sun rises on my right, that I must be driving north instead of south... because I recognize that my belief that I am driving south is inconsistent with that observation, together with what I know about the direction of rotation of the earth. I abandon the belief because I recognize that it could not be true.... I oppose the abolition of the inheritance tax... because I recognize that the design of property rights should be sensitive not only to autonomy but also to fairness...

Game, set, match, and tournament!"

That last sentence, which is Brad's, seems revealing of a mindset that sometimes creeps into his writing in his blog, less aimed at truth than at victory in some argumentative competition. I like a lot of what he does on his blog, but that attitude, and the related one that reads like an attempt to exhibit his hip and with-it-ness by using internet jargon that the unhip like me have to google ("self-pwnage", which Callahan is said to have committed), are not so appealing. The "transcendent direct access" I have already argued is mostly a straw-man of Brad's own creation, Nagel's point being primarily that (as says immediately following what Brad has quoted) "As the saying goes, I operate in the space of reasons." One aspect of operating in the space of reasons is trying to preserve some consistency between ones various beliefs; that seems to be the nub of the driving example (but we should not forget the important point that there is more than just deductive logic going on here... we have to decide which of the contradictory beliefs to give up). And we are also to some extent doing so (preserving consistency) in the case of the inheritance tax, though the full argument in this case is likely to be much more involved and less clear than in the case of the driving example. Nagel is arguing that we try to square our beliefs about the particular case of the inheritance tax with general beliefs that we (may) hold about how social institutions like property rights should be designed. Focusing on this consistency issue, though, can --- in both factual and ethical situations --- obscure the essential role of factors other than mere consistency in the process of reasoning about what beliefs to hold. As I mentioned in earlier posts, Nagel gives this somewhat short shrift, notably by not discussing inductive reasoning much, though he's clear about the fact that it's needed. But it's remarkable that DeLong---who I would guess shares Nagel's views on the inheritance tax, and possibly even his reasons (although he may also find some strength in arguments involving "social welfare functions) should think that this passage grounds an immediate declaration of victory. I guess it's because he wrongly thinks the issue is about "direct transcendent access".

Even more remarkable is philosopher Simon Blackburn's very similar reaction---if, as I am guessing, his example of "why income distribution in the US is unjust" is prompted in part by Nagel's reference to the inheritance tax. There are points I agree with in Blackburn's article, but then there is this:

According to Nagel, Darwinians can explain, say, why we dislike pain and seek to minimize bringing it about for ourselves and for others we love. But, Nagel thinks, for the Darwinian, its “real badness” can be no part of the explanation of why we are averse to it. So it is another mystery how real badness and other real normative properties enter our minds. Nagel here manifests his founding membership of a peculiar and fortunately local philosophical subculture that thrives by resolutely dismissing the resources of the alternative, Humean picture, which sees our judgement that pain is a bad thing as a useful expression of our natural aversion to it. All he says about this is that it “denies that value judgements can be true in their own right”, which he finds implausible. He is silent about why he thinks this, perhaps wisely, if only because nobody thinks that value judgements are true in their own right. The judgement that income distribution in the US is unjust, for instance, is not true in its own right. It is true in virtue of that fact that after decades of lobbying, chief executives of major companies earn several hundred times the income of their rank-and-file workers. It is true because of natural facts.

Parenthetically, but importantly: I agree with Blackburn's characterization of Nagel as believing that the "real badness"
of pain cannot be a main part of a Darwinian explanation of our aversion to pain. And I disagree with this belief of Nagel's.

However, I don't know what's so peculiar and local about resolutely dismissing (sometimes with plenty of discussion, though one virtue of Nagel's book is that it is short, so a point like this may not get extensive discussion) the Humean view here that this badness is just "natural aversion".  But in any case, Blackburn's discussion of his example is truly weird.  It seems reasonable to view a statement like "income distribution in the US is unjust" as true both because of the "natural facts" Blackburn cites, which explain how it has come to be what it is, and because of the component where the actual "values" come in, which give reasons for our belief that this high degree of inequality, is in fact unjust.  True, according to some theories of justice, e.g. a libertarian one, the genesis of a pattern of income and wealth distribution may be germane to whether or not it is just.  Blackburn might be adducing such an explanation, since he mentions "lobbying" as a cause (and not, say "hard work").  But if so, he still hasn't explained: what's wrong with lobbying?  Why does it cast doubt on the justice of the resulting outcome?  What Nagel means by value judgements being true "in their own right" is not likely that every statement with a value component, like Blackburn's about US income and wealth distribution, is true in and of itself and no reasons can be given for it.  What I think he means is that at some point, probably at many different points, there enters into our beliefs about matters of value an element of irreducible judgement that something is right or wrong, good or bad, and that this is objective, not just a matter of personal taste or "natural aversion".  What Blackburn's statement reads most like, due to his emphasis on "natural facts", is an attempt to substitute the causal factors leading to US income distribution being what it is, for the moral and political considerations---quite involved, perhaps subtle, and certainly contentious---that have led many to judge that it should not be what it is.  It's quite clear from Nagel's discussion of the inheritance tax what he thinks some of those considerations are: "autonomy and fairness". I just don't understand how someone could think that Blackburn's discussion of why US income distribution is unjust is better than an account in terms of concepts like autonomy and fairness---the sort of account that Nagel would obviously give. I've gotten some value from parts of Blackburn's work, even parts of this article, but this part---if this reading is correct---seems monumentally misguided.  Or does he think that the rest of the explanation is that human beings just have a "natural aversion" to income distribution that is as unequal, or perhaps as influenced by lobbying, as the US's currently is.  But you might think that a cursory look at a large part of the Republican party in the US would have disabused him of that notion.

Perhaps I'm being excessively snarky here...advocates, like Blackburn, of the natural aversion view would probably argue that it needs to be supplemented and modified by reasoning.... perhaps it is just that the "irreducibly moral", as opposed to the deductive/analogical reasoning component, of this process, is still just a matter of natural aversion.  I would think more Hobbesian considerations would come into play as well, but that is a matter for (you may be sorry to hear) another post.

Russell Blackford on Thomas Nagel on "objective values"

Posted on by

Russell Blackford formulates what he thinks is Thomas Nagel's argument for "the existence of objective values".  I think I disagree with Blackford on this.  Blackford's point seems to be that although he doesn't want to die a premature death, or suffer horrible torture, it wouldn't really be bad if he did.  Or at least, that he is not logically committed to thinking it would be.  Perhaps the logical point is correct, I'm not sure.  I would have to figure out what the difference is between valuing something and thinking it is really valuable.  I'm kind of suspicious of this supposed difference, but I suppose it merits close thought.  (References, anyone?) How does it differ from the difference between thinking the cat is on the mat and thinking the cat is really on the mat?  True, there is the difference, in Blackford's formulation, between "valuing X" and "thinking X is valuable".  Is that the crucial bit of Blackford's argument?  Or, since we're concerned with practical reason here, is to state or think or that one values something just to state that or think that one will take action to bring it about, but not to make the "deontic" statement that it should come about?  (All subject to qualifications about other things being equal, or about how it should be traded off with other things valued, of course.)  But even if this distinction makes sense, which it may well do, I think Nagel would argue... and I would follow him... that most of us just DO not only value certain things, but think that those things really are valuable.

Nagel and Delong II: Fallibility and Transcendence

Posted on by

In my first post on Brad Delong's series of criticisms of Thomas Nagel's new book Mind and Cosmos I focused not on Brad's initial critcism but on a later post that seemed to be implying Nagel put too much weight on "common sense".  In this post I'll focus on Brad's initial criticism, and in particular on what seems to me his misunderstanding of Nagel's arguments concerning reason, as crucially dependent on the notion that reason is infallible at least in some cases.

Brad's critique began with a reaction to some remarks by Tyler Cowen, in particular Cowen's assertion that "People will dismiss his [Nagel's] arguments to remain in their comfort zone, while temporarily forgetting he is smarter than they are and furthermore that many of their views do not make sense or cohere internally."

Now I think it is unfortunate that Cowen is speculating about who's "smarter than" who, and unfortunate that Brad joins him in doing so.  Everyone involved seems to be quite smart, but unfortunately Brad seems to me to be misunderstanding what the main thrust of Nagel's argument is, and where its main weakness lies.  DeLong reacts to Cowen:

And here Tyler appears to me to have gone off the rails. Thomas Nagel is not smarter than we are--in fact, he seems to me to be distinctly dumber than anybody who is running even an eight-bit virtual David Hume on his wetware.

He fixates on a single example taken from Nagel's book and, I think, fails to understand the role Nagel thinks this example plays. Brad seems to think it is crucial that Nagel view reason as infallible. "And my certainty that I know must be correct!" as he puts it in his gloss on Nagel:

Nagel's argument, to the extent that I understand it and that it is coherent, goes roughly like this:

Suppose we think we are going south-southwest and see the sun rising before us. We don't think: "the heuristics of reasoning that have evolved because they tend to boost reproductive fitness conclude that it is very likely that I am not in fact going south-southwest". We think, instead: "I know that the sun rises in front of me when I am going east! Either I am hallucinating, or I must be going roughly east! I deduce this by my reason, and my reason is a mechanism that can see that the algorithm it follows is truth-preserving! My mind is in immediate contact with the rational order of the universe! I don't just think I am going east! I know I am either hallucinating or going east! And my certainty that I know must be correct! And I know that my certainty must be correct--and that triumph of reason cannot be given a purely physical explanation! Since I believe I am not hallucinating, I abandon the belief that I am going south-southwest because of my reason's transcendent grasp of objective reality! My consciousness is an instrument of transcendence that grasps objective reality! And no blind evolutionary process can produce such a transcendent instrument!"

Aspects of this example of Nagel's bothered me as well, but it plays a much less central part in Nagel's book than you might think from Brad's gloss. Note that even the material in quotes is a gloss, not a quote from Nagel, although it draws fairly heavily on him. (Further down in this post, I quote the passage in Nagel from the first appearance of the example to the last explicit reference to it.  Brad's post also contains further material on the general topic of reason directly quoted from Nagel.)  In the context of Brad's post, the term "Nagel's argument" seems to imply that this is the main argument of the book, on which it stands or falls.

As I said, I don't think the example is central. Rather, it is intended as an example of something central to the book, which is the claim that reason has the power --- imperfect and fallible, to be sure --- to get us in touch with objective reality, in a way that helps us transcend the appearance of things from our own particular viewpoint or perspective. It is probably also intended as part of a discussion of how logic --- the avoidance of contradiction --- is an essential part of our ability to engage in more subtle and substantive forms of reasoning. I will discuss this second point later, concentrating for the moment on the first.

Nagel is extremely clear that he does not believe that reason's power to help get us in touch with objective reality is infallible. (See the next quote I display from Nagel for an utterly explicit statement of this.)  It may seem that he is claiming it to be infallible in driving example, but even if he is, that does not seem crucial to his main line of argument. Most of Brad's ridicule of Nagel's argument is directed against the claim of infallibility, so it just misses its target if by "Nagel's argument" is meant, as is clear from the context, the overall line of argument of Nagel's book.

The overall argument of the book is not a single line of reasoning. But some main strands concern the nature and origin of life, of consciousness, and---what is under discussion here----of reason. Here is how Nagel puts his main argument concerning the nature of reason:

Thought and reasoning are correct or incorrect in virtue of something independent of the thinker's beliefs, and even independent of the community of thinkers to which he belongs. We take ourselves to have the capacity to form true beliefs about the world around us, about the timeless domains of logic and mathematics, and about the right thing to do. We don't take these capacities to be infallible, but we think they are often reliable, in an objective sense, and that they can give us knowledge. [Mind and Cosmos, pp. 80-81]

Perhaps some confusion has arisen because of Nagel's use of the word "reliable" elsewhere in the book (e.g. in the excerpt DeLong quotes)...it should not be taken to imply infallibility. In Brad's favor, the "directness" with which Nagel says reason "puts us in touch with the rational order of things" in this particular example, is thought by Nagel to strengthen his case. I just don't think it's the main point.

Lest anyone misunderstand, I don't agree with Nagel that our understanding of reason as part of a process enabling us to --- fallibly, Nagel admits, and partially, I might add --- get in touch with an objective reality that transcends each of our particular perspectives on it, provides support to the view that reason could not have evolved through natural selection.

Brad goes on to propose a counterexample to the claim that the bit of reasoning in Nagel's example is infallible. It is that "During northern hemisphere winter, if you are near the North Pole, it is perfectly possible to see the sun rise due south if you are due solar north of the center of the earth as you come out of the Earth's shadow. And I was. And I did."

Several things can be said about this. The most important one is that Nagel need not and does not claim infallibility. Less important is that Nagel explicitly described his example as one in which "I am driving...". Brad was flying. So Brad's "it happened to me" is not literally true. Moreover the distinction between flying and driving is not an irrelevant one (like that between its being Nagel or DeLong who is doing the reasoning...) but one that is probably relevant. I don't know whether there are any roads near enough the north pole that one could, driving, have the experience Brad did. Perhaps there is land, or at certain times of the year, perhaps there is still enough sea ice, near enough the pole that one could do this off-road, by driving a long way off-road, or bringing a vehicle in by air. Or perhaps not. I really don't think it matters much. There are some background assumptions that are not made explicit, though suggested by the framing of the situation, as there are in most pieces of reasoning.

Here's Nagel's introduction of the example, and its sequel:

But suppose I observe a contradiction among my beliefs and "see" that I must give up at least one of them. (I am driving south in the early morning and the sun rises on my right.) In that case, I see that the contradictory beliefs cannot all be true, and I see it simply because it is the case. I grasp it directly. It is not adequate to say that, faced with a contradiction, I feel the urgent need to alter my beliefs to escape it, which is explained by the fact that avoiding contradictions, like avoiding snakes and precipices, was fitness-enhancing for my ancestors. That would be an indirect explanation of how the impossibility of the contradiction explains my belief that it cannot be true. But even if some of our ancestors were prey to mere logical phobias and instincts, we have gone beyond that: We reject a contradiction just because we see that it is impossible, and we accept a logical entailment just because we see that it is necessarily true.

In ordinary perception, we are like mechanisms governed by a (roughly) truth-preserving algorithm. But when we reason, we are like a mechanism that can see that the algorithm it follows is truth-preserving. Something has happened that has gotten our minds into immediate contact with the rational order of the world, or at least with the basic elements of that order, which can in turn be used to reach a great deal more. That enables us to possess concepts that display the compatibility or incompatibility of particular beliefs with general hypotheses. We have to start by regarding our prereflective impressions as a partial and perspectival view of the world, but we are then able to use reason and imagination to construct candidates for a larger conception that can contain and account fo that part. This applies in the domain of value as well as of fact. The process is highly fallible, but it could not even be attempted without this hard core of self-evidence, on which all less certain reasoning depends. In the criticism and correction of reasoning, the final court of appeal is always reason itself.

What this means is that if we hope to include the human mind in the natural order, we have to explain not only consciousness as it enters into perception, emotion, desire, and aversion but also the conscious control of belief and conduct in response to the awareness of reasons---the avoidance of inconsistency, the subsumption of particular cases under general principles, the confirmation or disconfirmation of general principles by particular observations, and so forth. This is what it is to allow oneself to be guided by the objective truth rather than just by one's impressions. It is a kind of freedom---the freedom that reflective consciousness gives us from the rule of innate perceptual and motivational dispositions together with conditioning. Rational creatures can step back from these influences and try to make up their own minds. I set aside the question whether this kind of freedom is compatible or incompatible with causal determinism, but it does seem to be something that cannot be given a purely physical analysis and therefore, like the more passive forms of consciousness, cannot be given a purely physical explanation either.

If I decide, when the sun rises on my right, that I must be driving north instead of south, it is because I recognize that my belief that I am driving south is inconsistent with that observation, together with what I know about the direction of rotation of the earth. I abandon the belief because I recognize that it couldn't be true. If I put money into a retirement account because the future income it generates will be more valuable to me than what I could spend it on now, I act because I see that this makes it a good thing to do. If I oppose the abolition of the inheritance tax, it is because I recognize that the design of property rights should be sensitive not only to autonomy but also to fairness. As the saying goes, I operate in the space of reasons.[Mind and Cosmos, pp. 91-92]

Gene Callahan criticizes Brad as follows:

So Nagel gives us two beliefs:
1) The sun rises in the east (where I am); and
2) I am driving south, which means the east will be on my left.
And a fact: But the sun is rising to my right!

So Nagel's point is that we cannot continue to hold 1) and 2) simultaneously: "I must give up at least one of them." How could he have said that more plainly?

Then Nagel goes on to state that "IF" (notice, that "if" is right in the original text, I did not add it!) he decides to give up belief 2), it will be because he sees he cannot logically hold 1) and 2) at the same time. Notice what the "if" implies: Nagel clearly understands that he has the option of giving up belief 1) instead! Otherwise, no point to the "if."

Now, Brad Delong comes along and says, "What an idiot! [And he really does insult Nagel like that.] Once, I was in that situation, and I had to give up belief 1)!"

Ahem. One does not disprove the proposition that one ought to give up at least one of two contradictory beliefs by showing how once, one gave up one of two contradictory beliefs.

Brad's response:

Nagel does not believe: "the sun rises in the east (where I am)." Nagel believes: "the sun rises on my right".

Thus the two beliefs that Nagel's reason tells him are in conflict are (a) his belief that he is going south, and (b) his belief he sees the sun rising on his right. The choice he gives himself is between concluding that he is going north and concludeingthat he is hallucinating.

Now I understand that Callahan wishes that Nagel were not Nagel but rather some Nagel' who had added a third belief: (c) "I am in a normal place (but there are weird places on earth where the sun rises in a non-standard way)."

But we go to argument with the Nagel we have, and not the Nagel' Callahan wishes we had.

Callahan would presumably say that Nagel was just being sloppy, and that there is actually an unsloppy Nagel' who had made the argument that Callahan wishes he had made, and whose reason does have transcendental access to objective reality, and that we should deal with the argument not of Nagel but of Nagel'.

But Callahan's confusion of the Nagel' he wishes we were talking about with the Nagel who we are talking about demonstrates my big point quite effectively: powerful evidence that Nagel is a jumped-up monkey using wetware evolved to advance his reproductive fitness, rather than a winged angelic reasoning being with transcendental access to objective reality. No?

I think Callahan is roughly right here. Roughly because it's not obviously correct that "Nagel gives us two beliefs". Callahan's (2) is stated in Nagel's parenthetical introduction of the example (see the quote above). But the parenthetical introduction is probably best read as describing the situation, not explicitly attributing beliefs ("I am driving south", not "I believe I am driving south"). It's clear we're to take as implicit that the subject of the example believes this, though, and when Nagel returns to the example later in the passage I quoted it is made explicit: this is the belief that is given up. That return to the example also makes it clear that there are background beliefs not initially mentioned in Nagel's parenthetical introduction of the example: Nagel mentions "what I know about the direction of rotation of the earth". This is presumably where Callahan gets number (2) namely "The sun rises in the east (where I am)." That seems a correct reading of Nagel, so DeLong's "Nagel does not believe: "the sun rises in the east (where I am)." Nagel believes: "the sun rises on my right"." just seems wrong.  The Nagel of the example believes both of these things (if we understand "the sun rises on my right" to mean something like "the sun is rising on my right".  Brad's misinterpretation is probably based on taking the parenthetical sentence introducing the example as a statement of the two beliefs that are in contradiction, rather than a sketch of a situation in which "I observe a contradiction in my beliefs". (Brad also changes Nagel's "driving south" to "going south", which affects, as I discussed above, whether Brad's flying experience is relevant.)

I think Nagel is getting at several things with this example, in light of the surrounding discussion.

(1) One is the idea that deductive reason helps us access truths about the world that go beyond our own particular perspective on it, because the avoidance of inconsistency is integral to the use of language, which in turn enables us to describe how the world is or might be from a point of view that is not just the perspective of one being that it makes possible. I am not sure what Brad means by "transcendent access" to objective reality--- it may just be a rhetorical flourish, liked "winged" and "angelic". The term "transcendent access" does not appear in Mind and Cosmos. When Nagel uses words with the root "transcend", he is referring to transcending a limited point of view to come up with a view of the world "as it is independently of the thinker's beliefs and even independently of the community of thinkers to which he belongs." (He also uses it---probably in the same sense---to refer to "a transcendent being", a notion he finds unappealing.) In his description of "what it is to be guided by the objective truth" toward the end of the long quote above, he is quite clear that this involves observations and (broadly speaking) "inductive" reasoning ("confirmation and disconfirmation"), and earlier he mentions "imagination" in addition to reasoning. (So if Brad's "Humean heuristics" just means inductive reasoning broadly construed, then it looks like Nagel's on board with it.) When reading the discussion of the driving example in Mind and Cosmos and related passages in The Last Word, I have sometimes felt puzzled about why Nagel seems to be laying such emphasis on deductive reasoning. And in general, I'm slightly frustrated by the relative lack of discussion of induction or related non-inductive aspects of scientific reasoning in Nagel's writings. But I think the quoted passages make clear that for Nagel, reason comprises induction too. I think the reason for his stress on deduction and consistency is the importance --- as Nagel sees it --- of language, and language's intimate link with logic --- to the very formulation of theories and hypotheses, scientific and otherwise. Nagel's emphasis on "directness" in simple cases may or may not be misplaced, but I don't think it's the linchpin of his broader argument.

(2) Secondly, and perhaps more controversially, Nagel believes that we must conceive of our reasoning as autonomous and free---that we cannot view it as a mere disposition. A mere disposition is how Hume, on one reading, viewed "induction", if not deduction... here I think Nagel would disagree with Hume, and perhaps with DeLong, if "mere disposition" is what DeLong means by "Humean heuristics". The key point, for Nagel, is that "In the criticism and correction of reasoning, the final court of appeal is always reason itself." The theory of evolution itself is part of that objective picture of reality, transcending our individual perspectives on it, that reason enables us to arrive at. For Nagel, it would be absurd to let a belief in evolution by natural selection undermine our view that our reasoning, in conjunction with imagination and observation, can get us in touch with and is getting us in touch with objective reality, because our very belief in evolution itself relies on this view. It is this, and not infallibility or "transcendent access" (a term Nagel never uses) that is the most important, and that I think is crucial to his broader argument.  Note that this does not automatically imply that a belief in evolution by natural selection cannot modify our assessment of our reasoning, perhaps leading us to view particular judgments or modes of reasoning as suspect, because arising from heuristics that we can see to be reliable only in certain situations similar to those in which they evolved.  Indeed, Nagel seems overly impressed with this possibility---one of his main grounds for rejection of the notion that there could be an evolutionary-biological explanation of the advent of reason in humans is his view that such an explanation would necessarily undermine our assessment that the reasoning we exercise in conjunction with our other faculties actually is, on balance, tending to get us in touch with objective reality.

Brad does address some of these issues, in response to Callahan's pointing out that they are the main ones; I will take up that part of their discussion in a later post.

Let me here take up an element of the quoted passage from Nagel that is bound to have raised some hackles.
Nagel: "I set aside the question whether this kind of freedom [to decide what to believe and how to act for reasons, i.e. by reasoning -- HB] is compatible or incompatible with causal determinism, but it does seem to be something that cannot be given a purely physical analysis and therefore, like the more passive forms of consciousness, cannot be given a purely physical explanation either."

This really is a key argument for Nagel. However, in my view, it needs to be understood in terms of the subtleties of emergence. As I have written elsewhere, I think there is some crucial unclarity in Nagel (or in my understanding of him) about what "purely physical explanation" might mean. If it means "explanation in terms of the concepts of physics" then I suspect that the hypothesis that "this kind of freedom [...] cannot be given a purely physical explanation [...]" is correct.  (However, I think I still have a substantive disagreement with Nagel on the meaning of "explanation".)   But if we allow an evolutionary biological evolution to use concepts like "reason" (which seems rather reasonable if one is going to try to explain the origin of our ability to reason), it seems to me that this is compatible with our eventually having an evolutionary-biological explanation of its historical origin. Here also I think I disagree with Nagel, who sometimes refers to "physics extended to include biology", suggesting that to him an evolutionary-biological explanation is a kind of purely physical explanation. I've discussed this some in my first post on Mind and Cosmos, and will discuss it more in future posts. There are deep and subtle philosophical and scientific questions involved, but in my view it is here if anywhere that Nagel goes importantly astray in dealing with reason, and not primarily in some actual or putative attribution of infallibility to simple judgements of contradiction, nor even in the notion (which Nagel does appear to subscribe to, but which I'm not sure I want to endorse) that the faculty of avoiding contradiction involves our minds being in "immediate contact with the rational order of things" [Mind and Cosmos, p. 91].

 

 

Nagel and DeLong I: Common Sense

Posted on by

Brad DeLong has been hammering --- perhaps even bashing --- away at Thomas Nagel's new book Mind and Cosmos (Oxford, 2012).  Here's a link to his latest blow. I think Nagel's wrong on several key points in that book, but I think Brad is giving people a misleading picture of Nagel's arguments.  This matters because Nagel has made very important points --- some of which are repeated in this book, though more thoroughly covered in his earlier The Last Word (Oxford, 1997) --- about the nature of reason, defending the possibility of achieving, in part through the use of reason, objectively correct knowledge (if that is the right word) in areas other than science, and giving us some valuable ideas about how this can work in particular cases, for example, in the case of ethics, in The Possibility of Altruism [Princeton, 1979].

In his latest salvo Brad suggests that "If you are going to reject any branch of science on the grounds that it flies in the face of common sense, require[s] us to subordinate the incredulity of common sense, is not based ultimately on common sense, or is a heroic triumph of ideological theory over common sense--quantum mechanics is definitely the place to start…".  This is preceded by some quotes from Nagel:

  • But it seems to me that, as it is usually presented, the current orthodoxy about the cosmic order is the product of governing assumptions that are unsupported, and that it flies in the face of common sense…
  • My skepticism is… just a belief that the available scientific evidence, in spite of the consensus of scientific opinion, does not… rationally require us to subordinate the incredulity of common sense…
  • Everything we believe, even the most far-reaching cosmological theories, has to be based ultimately on common sense, and on what is plainly undeniable…
  • I have argued patiently against the prevailing form of naturalism, a reductive materialism that purports to capture life and mind through its neo-Darwinian extension…. I find this view antecedently unbelievable— a heroic triumph of ideological theory over common sense…

Now there are things I disagree with here, but Nagel is clearly not claiming that no theory that is not itself a piece of common sense is acceptable. Indeed, the second bullet point makes it clear that he allows for the possibility that scientific evidence could "rationally require" him to subordinate the incredulity of common sense. It is his judgment that it does not in this case. Now---at least with regard to the possibility of an explanation by evolutionary biology of the emergence of life, consciousness, and reason on our planet and in our species, which is what I think is at issue--- I don't share his incredulity, and I also suspect that I would weigh the scientific evidence much more heavily against such incredulity, if I did share some of it.  But Nagel is not commited to a blanket policy of "reject[ing] scientific theories because they fail to match up to your common sense." Regarding the third bullet point, it's perhaps stated in too-strong terms, but it's far from a claim that every scientific theory can directly be compared to common sense and judged on that basis. The claim that scientific theories are "ultimately based in common sense and on what is plainly undeniable" does not imply that this basis must be plain and direct. Logic and mathematics develop out of common-sense roots, counting and speaking and such... science develops to explain "plainly undeniable" results of experiments, accounts of which are given in terms of macroscopic objects... Some of this smacks a bit too much of notions that may have proved problematic for positivism ("plainly undeniable" observation reports?)... but the point is that common sense carries some weight and indeed is a crucial element of our scientific activities, not that whatever aspect of "common sense" finds quantum theory hard to deal with must outweigh the enormous weight of scientific experience and engineering practice, also rooted "ultimately" according to Nagel in common sense, in favor of that theory.

Just for the record I don't find that the bare instrumentalist version of quantum theory as an account of the probabilities of experimental results "flies in the face of common sense" --- but it does seem that it might create serious difficulty for the conception of physical reality existing independent of our interactions with it. At any rate it does not seem to provide us with a picture of that sort of physical reality (unless you accept the Bohm or Everett interpretations), despite what one might have hoped for from a formalism that is used to describe the behavior of what we tend to think of as the basic constituents of physical reality, the various elementary particles or better, quantum fields.  But if someone, say Nagel, did believe that this all flies in the face of common sense, it would be open to him to say that in this case, we are permitted, encourage, or perhaps even required to fly in said face by the weight of scientific evidence.

As I've said, I disagree on two counts with Nagel's skepticism about an evolutionary explanation of mind and reason: it doesn't fly in the face of my common sense, and I weigh the evidence as favoring it more strongly than does Nagel. Part of my disagreement may be that what Nagel has in mind is an evolutionary explanation that is commited to a "reductive materialism that purports to capture life and mind through its neo-Darwinian extension." Whereas I have in mind a less reductive approach, in which consciousness and reason are evolutionarily favored because they have survival value, but we do not necessarily reduce these concepts themselves to physical terms. In my view, biology is rife with concepts that are not physical, nor likely to be usefully reduced to physical terms--- like, say, "eye". As with "eye", there may be no useful reduction of "consciousness" or "perception" or "thought" or "word" or "proposition", etc.., to physics, but I don't think that implies that the appearance of such things cannot have an evolutionary explanation. (Nor, just to be clear, does it imply that these things are not realized in physical processes.) So I might share Nagel's incredulity that such things could have a "materialist" explanation, if by this he means one in terms of physics, but not his incredulity about evolutionary explanations of the appearance of mind and reason. To me, it seems quite credible that these phenomena form part of the mental aspect of structures made of physical stuff, though we will never have full explanations for all the phenomena of consciousness and the doings of reason, in terms of this physical structure.

(David Deutsch's recent book The Beginning of Infinity is one excellent source for understanding such non-reductionism---see in particular its Chapter 5, "The Reality of Abstractions".)

I'll likely make several more posts on this business, both on other ways in which I think Brad and others have mischaracterized Nagel's arguments or misplaced the emphasis in their criticisms, and on why this matters because some important points that Nagel has made on matters closely related to these, that I think have value, are in danger of being obscured, caricatured, or dismissed under the influence of the present discussion by Brad and others.

Thomas Nagel's "Mind and Cosmos"

Posted on by

I've just finished reading Thomas Nagel's newish book, "Mind and Cosmos" (Oxford, 2012).  It's deeply flawed, but in spite of its flaws some of the points it makes deserve more attention, especially in the broader culture, than they're likely to receive in the context of a book that's gotten plenty of people exercised about its flaws.  I'm currently undecided about whether to recommend reading his book for these points, as they are probably made, without the distracting context and possibly better formulated, equally well elsewhere, notably in Nagel's  "The Last Word" (Oxford, 1997).  The positive points are the emphasis on the reality of mental phenomena and (more controversially) their ireducibility to physical or even biological terms, the unacceptability of viewing the activities of reason in similarly reductive terms, and a sense that mind and reason are central to the nature of reality.  Its greatest flaws are an excessively reductionist view of the nature of science, and, to some degree in consequence of this, an excessive skepticism about the potential for evolutionary explanations of the origins of life, consciousness, and reason.

One of the main flaws of Nagel's book is that he seems --- very surprisingly --- to view explananations in terms of, say, evolutionary biology, as "reductively materialist".  He seems not to appreciate the degree to which the "higher" sciences involve "emergent" phenomena, not reducible---or not, in any case, reduced---to the terms of sciences "below" them in the putative reductionist hierarchy.  Of course there is no guarantee that explanations in terms of these disciplines' concepts will not be replaced by explanations in terms of the concepts of physics, but it has not happened, and may well never happen.  The rough picture is that the higher disciplines involve patterns or structures formed, if you like, out of the material of the lower ones, but the concepts in terms of which we deal with these patterns or structures are not those of physics, they are higher-order ones.  And these structures and their properties---described in the language of the higher sciences, not of physics---are just as real as the entities and properties of physics.  My view --- and while it is non-reductionist, I do not think it is hugely at variance with that of many, perhaps most, scientists who have considered the matter carefully --- is that at a certain very high level, some of these patterns have genuine mental aspects.  I don't feel certain that we will explain, in some sense, all mental phenomena in terms of these patterns, but neither does it seem unreasonable that we might.  ("Explanation" in this sense needn't imply the ability to predict perfectly (or even very well), nor, as is well known, need the ability to predict perfectly be viewed as providing us with a full and adequate explanation---simulation, for example, is not necessarily understanding.)   Among scientists and philosophers who like Nagel hold a broadly "rationalist" worldview David Deutsch, in his books The Fabric of Reality and especially The Beginning of Infinity, is much more in touch with the non-reductionist nature of much of science.

Note that none of this means there isn't in some sense a "physical basis" for mind and reason.  It is consistent with the idea that there can be "no mental difference without a physical difference", for example (a view that I think even Nagel, however, agrees with).

This excessively reductionist view of modern science can also be found among scientists and popular observers of science, though it is far from universal.   It is probably in part, though only in part, responsible for two other serious flaws in Nagel's book.  The first of these is his skepticism about the likelihood that we will arrive at an explanation of the origin of life in terms of physics, chemistry, and perhaps other sciences that emerge from them---planetary science, geology, or perhaps some area on the borderline between complex chemistry and biology that will require new concepts, but not in a way radically different from the way these disciplines themselves involve new concepts not found in basic physics.  The second is his skepticism that the origins of consciousness and reason can be explained primarily in terms of biological evolution.  I suspect he is wrong about this.  The kind of evolutionary explanation I expect is of course likely to use the terms "consciousness" and "reason" in ways that are not entirely reductive.   I don't think that will prevent us from understanding them as likely to evolve through natural selection.   I expect we will see that to possess the faculty of reason, understood (with Nagel) as having the---fallible, to be sure!---power to help get us in touch with a reality that transcends, while including, our subjective point of view, confers selective advantage.  Nagel is aware of the possibility of this type of explanation but --- surprisingly, in my view --- views it as implausible that it should be adaptive to possess reason in this strong sense, rather than just some locally useful heuristics.

The shortcomings in his views on evolution and the potential for an evolutionary explanation of life, consciousness, and reason deserve more discussion, but I'll leave that for a possible later post.

The part of Nagel's worldview that I like, and that may go underappreciated by those who focus on his shortcomings, is, as I mentioned above, the reality of the mental aspect of things, and the need to take seriously the view that we have the power, fallible as it may be, to make progress toward the truth about how reality is, about what is good, and about what is right and wrong.  I also like his insistence that much is still unclear about how and why this is so.  But to repeat, I think he's somewhat underplaying the potential involvement of evolution in an eventual understanding of these matters.  He may also be underplaying something I think he laid more stress on in previous books, notably The View from Nowhere and the collection of papers and essays Mortal Questions: the degree to which there may be an irreconcilable tension between the "inside" and "outside" views of ourselves.  However, his attitude here is to try to reconcile them. Indeed, one of the more appealing aspects of his worldview as expressed in both Mind and Cosmos and The Last Word is the observation that my experience "from inside" of what it is to be a reasoning subject, involves thinking of myself as part of a larger objective order and trying to situate my own perspective as one of many perspectives, including those of my fellow humans and any other conscious and reasoning beings that exist, upon it.  It is to understand much of my reasoning as attempting, even while operating as it must from my particular perspective, to gain an understanding of this objective reality that transcends that perspective.

So far I haven't said much about the positive possibilities Nagel moots, in place of a purely biological evolutionary account, for explaining the origin of life, consciousness, and reason.  These are roughly teleological, involving a tendency "toward the marvelous".  This is avowedly a very preliminary suggestion.  My own views on the likely role of mind and reason in the nature of reality, even more tentative than Nagel's, are that it is less likely that it arises from a teleological tendency toward the marvelous than that a potential for consciousness, reason, and value is deeply entwined with the very possibility of existence itself.  Obviously we are very far from understanding this.  I would like to think this is fairly compatible with a broadly evolutionary account of the origin of life and human consciousness and reasoning on our planet, and with the view that we're made out of physical stuff.