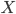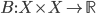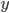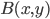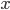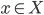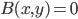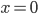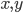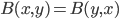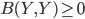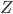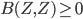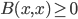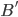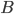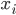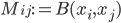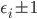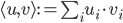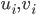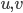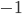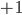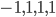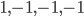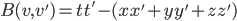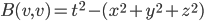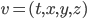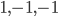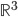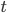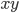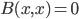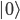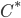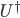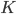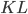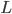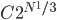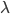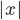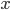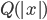Category Archives: Physics

No new enlightenment: A critique of "quantum reason"

Posted on by

I have a lot of respect for Scientific American contributing physics editor George Musser's willingness to solicit and publish articles on some fairly speculative and, especially, foundational, topics whether in string theory, cosmology, the foundations of quantum theory, quantum gravity, or quantum information.  I've enjoyed and learned from these articles even when I haven't agreed with them.  (OK, I haven't enjoyed all of them of course... a few have gotten under my skin.)  I've met George myself, at the most recent FQXi conference; he's a great guy and was very interested in hearing, both from me and from others, about cutting-edge research.  I also have a lot of respect for his willingness to dive in to a fairly speculative area and write an article himself, as he has done with "A New Enlightenment" in the November 2012 Scientific American (previewed here).  So although I'm about to critique some of the content of that article fairly strongly, I hope it won't be taken as mean-spirited.  The issues raised are very interesting, and I think we can learn a lot by thinking about them; I certainly have.

The article covers a fairly wide range of topics, and for now I'm just going to cover the main points that I, so far, feel compelled to make about the article.  I may address further points later; in any case, I'll probably do some more detailed posts, maybe including formal proofs, on some of these issues.

The basic organizing theme of the article is that quantum processes, or quantum ideas, can be applied to situations which social scientists usually model as involving the interactions of "rational agents"...or perhaps, as they sometimes observe, agents that are somewhat rational and somewhat irrational.  The claim, or hope, seems to be that in some cases we can either get better results by substituting quantum processes (for instance, "quantum games", or "quantum voting rules") for classical ones, or perhaps better explain behavior that seems irrational.  In the latter case, in this article, quantum theory seems to be being used more as a metaphor for human behavior than as a model of a physical process underlying it.  It isn't clear to me whether we're supposed to view this as an explanation of irrationality, or in some cases as the introduction of a "better", quantum, notion of rationality.  However, the main point of this post is to address specifics, so here are four main points; the last one is not quantum, just a point of classical political science.

 

(1) Quantum games.  There are many points to make on this topic.  Probably most important is this one: quantum theory does not resolve the Prisoner's Dilemma.  Under the definitions I've seen of "quantum version of a classical game", the quantum version is also a classical game, just a different one.  Typically the strategy space is much bigger.  Somewhere in the strategy space, typically as a basis for a complex vector space ("quantum state space") of strategies, or as a commuting ("classical") subset of the possible set of "quantum actions" (often unitary transformations, say, that the players can apply to physical systems that are part of the game-playing apparatus), one can set things up so one can compare the expected payoff of the solution, under various solution concepts such as Nash equilibrium, for the classical game and its "quantum version", and it may be that the quantum version has a better result for all players, using the same solution concept.  This was so for Eisert, Lewenstein, and Wilkens' (ELW for short) quantum version of Prisoner's Dilemma.  But this does not mean (nor, in their article, did ELW claim it did) that quantum theory "solves the Prisoner's Dilemma", although I suspect when they set out on their research, they might have had hope that it could.  It doesn't because the prisoners can't transform their situation into quantum prisoners dilemma; to play that game, whether by quantum or classical means, would require the jailer to do something differently.  ELW's quantum prisoner's dilemma involves starting with an entangled state of two qubits.  The state space consists of the unit Euclidean norm sphere in a 4-dimensional complex vector space (equipped with Euclidean inner product); it has a distinguished orthonormal basis which is a product of two local "classical bases", each of which is labeled by the two actions available to the relevant player in the classical game.  However the quantum game consists of each player choosing a unitary operator to perform on their local state.  Payoff is determined---and here is where the jailer must be complicit---by performing a certain two-qubit unitary---one which does not factor as a product of local unitaries---and then measuring in the "classical product basis", with payoffs given by the classical payoff corresponding to the label of the basis vector corresponding to the result.  Now, Musser does say that "Quantum physics does not erase the original paradoxes or provide a practical system for decision making unless public officials are willing to let people carry entangled particles into the voting booth or the police interrogation room."  But the situation is worse than that.  Even if prisoners could smuggle in the entangled particles (and in some realizations of prisoners' dilemma in settings other than systems of detention, the players will have a fairly easy time supplying themselves with such entangled pairs, if quantum technology is feasible at all), they won't help unless the rest of the world, implementing the game, implements the desired game, i.e. unless the mechanism producing the payoffs doesn't just measure in a product basis, but implements the desired game by measuring in an entangled basis.  Even more importantly, in many real-world games, the variables being measured are already highly decohered; to ensure that they are quantum coherent the whole situation has to be rejiggered.  So even if you didn't need the jailer to make an entangled measurement---if the measurement was just his independently asking each one of you some question---if all you needed was to entangle your answers---you'd have to either entangle your entire selves, or covertly measure your particle and then repeat the answer to the jailer.  But in the latter case, you're not playing the game where the payoff is necessarily based on the measurement result: you could decide to say something different from the measurement result.  And that would have to be included in the strategy set.

There are still potential applications:  if we are explicitly designing games as mechanisms for implementing some social decision procedure, then we could decide to implement a quantum version (according to some particular "quantization scheme") of a classical game.  Of course, as I've pointed out, and as ELW do in their paper, that's just another classical game.  But as ELW note, it is possible---in a setting where quantum operations (quantum computer "flops") aren't too much more expensive than their classical counterparts---that playing the game by quantum means might use less resources than playing it by simulating it classically.  In a mechanism design problem that is supposed to scale to a large number of players, it even seems possible that the classical implementation could scale so badly with the number of players as to become infeasible, while the quantum one could remain efficient.  For this reason, mechanism design for preference revelation as part of a public goods provision scheme, for instance, might be a good place to look for applications of quantum prisoners-dilemma like games.  (I would not be surprised if this has been investigated already.)

Another possible place where quantum implementations might have an advantage is in situations where one does not fully trust the referee who is implementing the mechanism.  It is possible that quantum theory might enable the referee to provide better assurances to the players that he/she has actually implemented the stated game.  In the usual formulation of game theory, the players know the game, and this is not an issue.  But it is not necessarily irrelevant in real-world mechanism design, even if it might not fit strictly into some definitions of game theory.  I don't have a strong intuition one way or the other as to whether or not this actually works but I guess it's been looked into.

(2) "Quantum democracy".  The part of the quote, in the previous item, about taking entangled particles into the voting booth, alludes to this topic.  Gavriel Segre has a 2008 arxiv preprint entitled "Quantum democracy is possible" in which he seems to be suggesting that quantum theory can help us the difficulties that Arrow's Theorem supposedly shows exist with democracy.  I will go into this in much more detail in another post.  But briefly, if we consider a finite set A of "alternatives", like candidates to fill a single position, or mutually exclusive policies to be implemented, and a finite set I of "individuals" who will "vote" on them by listing them in the order they prefer them, a "social choice rule" or "voting rule" is a function that, for every "preference profile", i.e. every possible indexed set of preference orderings (indexed by the set of individuals), returns a preference ordering, called the "social preference ordering", over the alternatives.  The idea is that then whatever subset of alternatives is feasible, society should choose the one mostly highly ranked by the social preference ordering,  from among those alternatives that are feasible.  Arrow showed that if we impose the seemingly reasonable requirements that if everyone prefers x to y, society should prefer x to y ("unanimity") and that whether or not society prefers x to y should be affected only by the information of which individuals prefer x to y, and not by othe aspects of individuals' preference orderings ("independence of irrelevant alternatives", "IIA"), the only possible voting rules are the ones such that, for some individual i called the "dictator" for the rule, the rule is that that individual's preferences are the social preferences.  If you define a democracy as a voting rule that satisfies the requirements of unanimity and IIA and that is not dictatorial, then "democracy is impossible".  Of course this is an unacceptably thin concept of individual and of democracy.  But anyway, there's the theorem; it definitely tells you something about the limitations of voting schemes, or, in a slighlty different interpretation, of the impossibility of forming a reasonable idea of what is a good social choice, if all that we can take into account in making the choice is a potentially arbitrary set of individuals' orderings over the possible alternatives.

Arrow's theorem tends to have two closely related interpretations:  as a mechanism for combining actual individual preferences to obtain social preferences that depend in desirable ways on individual ones, or as a mechanism for combining formal preference orderings stated by individuals, into a social preference ordering.  Again this is supposed to have desirable properties, and those properties are usually motivated by the supposition that the stated formal preference orderings are the individuals' actual preferences, although I suppose in a voting situation one might come up with other motivations.  But even if those are the motivations, in the voting interpretation, the stated orderings are somewhat like strategies in a game, and need not coincide with agents' actual preference orderings if there are strategic advantages to be had by letting these two diverge.

What could a quantum mitigation of the issues raised by Arrow's theorem---on either interpretation---mean?  We must be modifying some concept in the theorem... that of an individual's preference ordering, or voting strategy, or that of alternative, or---although this seems less promising---that of individual---and arguing that somehow that gets us around the problems posed by the theorem.  None of this seems very promising, for reasons I'll get around to in my next post.  The main point is that if the idea is similar to the --- as we've seen, dubious --- idea that superposing strategies can help in quantum games, it doesn't seem to help with interpretations where the individual preference ordering is their actual preference ordering.  How are we to superpose those?  Superposing alternatives seems like it could have applications in a many-worlds type interpretation of quantum theory, where all alternatives are superpositions to begin with, but as far as I can see, Segre's formalism is not about that.  It actually seems to be more about superpositions of individuals, but one of the big motivational problems with Segre's paper is that what he "quantizes" is not the desired Arrow properties of unanimity, independence of irrelevant alternatives, and nondictatoriality, but something else that can be used as an interesting intermediate step in proving Arrow's theorem.  However, there are bigger problems than motivation:  Segre's main theorem, his IV.4, is very weak, and actually does not differentiate between quantum and classical situations.  As I discuss in more detail below, it looks like for the quantum logics of most interest for standard quantum theory, namely the projection lattices of of von Neumann algebras, the dividing line between ones having what Segre would call a "democracy", a certain generalization of a voting rule satisfying Arrow's criteria, and ones that don't (i.e. that have an "Arrow-like theorem") is not commutativity versus noncommutativity of the algebra (ie., classicality versus quantumness), but just infinite-dimensionality versus finite-dimensionality, which was already understood for the classical case.  So quantum adds nothing.  In a later post, I will go through (or post a .pdf document) all the formalities, but here are the basics.

Arrow's Theorem can be proved by defining a set S of individuals to be decisive if for every pair x,y of alternatives, whenever everyone in S prefers x to y, and everyone not in x prefers y to x, society prefers x to y.  Then one shows that the set of decisive sets is an ultrafilter on the set of individuals.  What's an ultrafilter?  Well, lets define it for an arbitrary lattice.  The set, often called P(I), of subsets of any set I, is a lattice (the relevant ordering is subset inclusion, the defined meet and join are intersection and union).   A filter---not yet ultra---in a lattice is a subset of the lattice that is upward-closed, and meet-closed.  That is, to say that F is a filter is to say that  if x is in F, and y is greater than or equal to x, then y is in F, and that if x and y are both in f, so is x meet y.  For P(I), this means that a filter has to include every superset of each set in the filter, and also the intersection of every pair of sets in the filter.  Then we say a filter is proper if it's not the whole lattice, and it's an ultrafilter if it's a maximal proper filter, i.e. it's not properly contained in any other filter (other than the whole lattice).  A filter is called principal if it's generated by a single element of the lattice:  i.e. if it's the smallest filter containing that element.  Equivalently, it's the set consisting of that element and everything above it.  So in the case of P(I), a principal filter consists of a given set, and all sets containing that set.

To prove Arrow's theorem using ultrafilters, one shows that unanimity and IIA imply that the set of decisive sets is an ultrafilter on P(I).  But it was already well known, and is easy to show, that all ultrafilters on the powerset of a finite set are principal, and are generated by singletons of I, that is, sets containing single elements of I.  So a social choice rule satisfying unanimity and IIA has a decisive set containing a single element i, and furthermore, all sets containing i are decisive.  In other words, if i favors x over y, it doesn't matter who else favors x over y and who opposes it: x is socially preferred to y.  In other words, the rule is dictatorial.  QED.

Note that it is crucial here that the set I is finite.  If you assume the axiom of choice (no pun intended ahead of time), then non-principal ultrafilters do exist in the lattice of subspaces of an infinite set, and the more abstract-minded people who have thought about Arrow's theorem and ultrafilters have indeed noticed that if you are willing to generalize Arrow's conditions to an infinite electorate, whatever that means, the theorem doesn't generalize to that situation.  The standard existence proof for a non-principal ultrafilter is to use the axiom of choice in the form of Zorn's lemma to establish that any proper filter is contained in a maximal one (i.e. an ultrafilter) and then take the set of subsets whose complement (in I) is finite, show it's a filter, and show it's extension to an ultrafilter is not principal.  Just for fun, we'll do this in a later post.  I wouldn't summarize the situation by saying "infinite democracies exist", though.  As a sidelight, some people don't like the fact that the existence proof is nonconstructive.

As I said, I'll give the details in a later post.  Here, we want to examine Segre's proposed generalization.  He defines a quantum democracy  to be a nonprincipal ultrafilter on the lattice of projections of an "operator-algebraically finite von Neumann algebra".  In the preprint there's no discussion of motivation, nor are there explicit generalizations of unanimity and IIA to corresponding quantum notions.  To figure out such a correspondence for Segre's setup we'd need to convince ourselves that social choice rules, or ones satisfying one or the other of Arrow's properties, are related one to one to their sets of decisive coalitions, and then relate properties of the rule (or the remaining property), to the decisive coalitions' forming an ultrafilter.  Nonprincipality is clearly supposed to correspond to nondictatorship.  But I won't try to tease out, and then critique, a full correspondence right now, if one even exists.

Instead, let's look at Segre's main point.  He defines a quantum logic as a non-Boolean orthomodular lattice.  He defines a quantum democracy as a non-principal ultrafilter in a quantum logic.  His main theorem, IV.4, as stated, is that the set of quantum democracies is non-empty.  Thus stated, of course, it can be proved by showing the existence of even one quantum logic that has a non-principal ultrafilter.  These do exist, so the theorem is true.

However, there is nothing distinctively quantum about this fact.  Here, it's relevant that Segre's Theorem IV.3 as stated is wrong.  He states (I paraphrase to clarify scope of some quantifiers) that L is an operator-algebraically finite orthomodular lattice all of whose ultrafilters are principal if, and only if, L is a classical logic (i.e. a Boolean lattice).  But this is false.  It's true that to get his theorem IV.4, he doesn't need this equivalence.  But what is a von Neumann algebra?  It's a *-algebra consisting of bounded operators on a Hilbert space, closed in the weak operator topology.  (Or something isomorphic in the relevant sense to one of these.) There are commutative and noncommutative ones.  And there are finite-dimensional ones and infinite-dimensional ones.  The finite-dimensional ones include:  (1) the algebra of all bounded operators on a finite-dimensional Hilbert space (under operator multiplication and complex conjugation), these are noncommutative for dimension > 1  (2) the algebra of complex functions on a finite set I (under pointwise multiplication and complex conjugation) and (3) finite products (or if you prefer the term, direct sums) of algebras of these types.  (Actually we could get away with just type (1) and finite products since the type (2) ones are just finite direct sums of one-dimensional instances of type (1).)   The projection lattices of the cases (2) are isomorphic to P(I) for I the finite set.  These are the projection lattices for which Arrow's theorem can be proved using the fact that they have no nonprincipal ultrafilters.  The cases (1) are their obvious quantum analogues.  And it is easy to show that in these cases, too, there are no nonprincipal ultrafilters.  Because the lattice of projections of a von Neumann algebra is complete, one can use  essentially the same proof as for the case of P(I) for finite I.  So for the obvious quantum analogues of the setups where Arrow's theorem is proven, the analogue of Arrow's theorem does hold, and Segre's "quantum democracies" do not exist.

Moreover, Alex Wilce pointed out to me in email that essentially the same proof as for P(I) with I infinite, gives the existence of a nonprincipal ultrafilter for any infinite-dimensional von Neumann algebra:  one takes the set of projections of cofinite rank (i.e. whose orthocomplementary projection has finite rank), shows it's a filter, extends it (using Zorn's lemma) to an ultrafilter, and shows that's not principal.  So (if the dividing line between finite-dimensional and infinite-dimensional von Neumann algebras is precisely that their lowest-dimensional faithful representations are on finite-dimensional Hilbert spaces, which seems quite likely) the dividing line between projection lattices of von Neumann algebras on which Segre-style "democracies" (nonprincipal ultrafilters) exist, is precisely that between finite and infinite dimension, and not that between commutativity and noncommutativity.  I.e. the existence or not of a generalized decision rule satisfying a generalization of the conjunction of Arrow's conditions has nothing to do with quantumness.  (Not that I think it would mean much for social choice theory or voting if it did.)

(3) I'll only say a little bit here about "quantum psychology".  Some supposedly paradoxical empirical facts are described at the end of the article.  When subjects playing Prisoner's Dilemma are told that the other player will snitch, they always (nearly always? there must be a few mistakes...) snitch.  When they are told that the other player will stay mum, they usually also fink, but sometimes (around 20% of the time---it is not stated whether this typical of a single individual in repeated trials, or a percentage of individuals in single trials) stay mum.  However, if they are not told what the other player will do, "about 40% of the time" they stay mum.  Emanuel Pothos and Jerome Busemeyr devised a "quantum model" that reproduced the result.  As described in Sci Am, Pothos interprets it in terms of destructive interference between (amplitudes associated with, presumably) the 100% probability of snitching when the other snitches and the 80% probability of snitching when they other does not that reduces the probability to 60% when they are not sure whether the other will snitch.  It is a model; they do not claim that quantum physics of the brain is responsible.  However, I think there is a better explanation, in terms of what Douglas Hofstadter called "superrationality", Nigel Howard called "metarationality", and I like to call a Kantian equilibrium concept, after the version of Kant's categorial imperative that urges you to act according to a maxim that you could will to be a universal law.  Simply put, it's the line of reasoning that says "the other guy is rational like me, so he'll do what I do.  What does one do if he believes that?  Well, if we both snitch, we're sunk.  If we both stay mum, we're in great shape.  So we'll stay mum."  Is that rational?  I dunno.  Kant might have argued it is.  But in any case, people do consider this argument, as well, presumably, as the one for the Nash equilibrium.  But in either of the cases where the person is told what the other will do, there is less role for the categorical imperative; one is being put more in the Nash frame of mind.  Now it is quite interesting that people still cooperate a fair amount of the time when they know the other person is staying mum; I think they are thinking of the other person's action as the outcome of the categorical imperative reasoning, and they feel some moral pressure to stay with the categorical imperative reasoning.  Whereas they are easily swayed to completely dump that reasoning in the case when told the other person snitched: the other has already betrayed the categorical imperative.  Still, it is a bit paradoxical that people are more likely to cooperate when they are not sure whether the other person is doing so;  I think the uncertainty makes the story that "he will do what I do" more vivid, and the tempting benefit of snitching when the other stays mum less vivid, because one doesn't know *for sure* that the other has stayed mum.  Whether that all fits into the "quantum metaphor" I don't know but it seems we can get quite a bit of potential understanding here without invoking.  Moreover there probably already exists data to help explore some of these ideas, namely about how the same individual behaves under the different certain and uncertain conditions, in anonymous trials guaranteed not to involve repetition with the same opponent.

Less relevant to quantum theory, but perhaps relevant in assessing how important voting paradoxes are in the real world, is an entirely non-quantum point:

(4)  A claim by Piergiorgio Odifreddi, that the 1976 US election is an example of Condorcet's paradox of cyclic pairwise majority voting, is prima facie highly implausible to anyone who lived through that election in the US.  The claim is that a majority would have favored, in two-candidate elections:

Carter over Ford (as in the actual election)

Ford over Reagan

Reagan over Carter

I strongly doubt that Reagan would have beat Carter in that election.  There is some question of what this counterfactual means, of course:  using polls conducted near the time of the election does not settle the issue of what would have happened in a full general-election campaign pitting Carter against Reagan.  In "Preference Cycles in American Elections", Electoral Studies 13: 50-57 (1994), as summarized in Democracy Defended by Gerry Mackie, political scientist Benjamin Radcliff analyzed electoral data and previous studies concerning the US Presidential elections from 1972 through 1984, and found no Condorcet cycles.  In 1976, the pairwise orderings he found for (hypothetical, in two of the cases) two-candidate elections were Carter > Ford, Ford > Reagan, and Carter > Reagan.  Transitivity is satisfied; no cycle.  Obviously, as I've already discussed, there are issues of methodology, and how to analyze a counterfactual concerning a general election.  More on this, perhaps, after I've tracked down Odifreddi's article.  Odifreddi is in the Sci Am article because an article by him inspired Gavriel Segre to try to show that such problems with social choice mechanisms like voting might be absent in a quantum setting.

Odifreddi is cited by Musser as pointing out that democracies usually avoid Condorcet paradoxes because voters tend to line up on an ideological spectrum---I'm just sceptical until I see more evidence, that that was not the case also in 1976 in the US.  I have some doubt also about the claim that Condorcet cycles are the cause of democracy "becoming completely dysfunctional" in "politically unsettled times", or indeed that it does become completely dysfunctional in such times.  But I must remember that Odifreddi is from the land of Berlusconi.  But then again, I doubt cycles are the main issue with him...

Physics and philosophy: a civil and enlightening discussion

Posted on by

So, more on physics and philosophy:  this discussion thread involving Wayne Myrvold, Vishnya Maudlin, and Matthew Leifer is a model of civil discussion in which it looks like mutual understanding is increased, and that should be enlightening, or at least clarifying, to "listeners".  Matthew makes a point I made in my previous post:

Matthew Leifer [...] Wayne, I disagree with you that studying the foundations of quantum theory is philosophy. It is physics, it is just that most physicists do not realize that it is physics yet. Of course, there are some questions of a more philosophical nature, but I would argue that the most fertile areas are those which are not obviously purely philosophy.

Wayne Myrvold (June 12 at 6:42am)

Ah, but Matt, but part of the main point of the post was that we shouldn’t worry too much about where we draw the boundaries between disciplines. It’s natural philosophy in the sense of Newton, not counted as physics by many physicists, and may one day will be regarded as clearly part of physics by the physics community—- does it really matter what we call it? [...]

Matthew's response: "Well, it matters a lot on a personal level if you are trying to get a job doing foundations of quantum theory in a physics department 🙂 More seriously, I think there is a distinction to be made between studying the foundations of a theory in order to better comprehend the theory as it presently exists and studying them in order to arrive at the next theory."

Matthew puts a smiley face on the first sentence, and continues "More seriously..." But I think this is more serious than he is letting on here. In my view, thinking about M-theory and string theory and thinking about the foundations of quantum theory are roughly evenly matched as far as their likelihood (by which I mean probability) of giving rise to genuine progress in our understanding of the world (I'd give quantum foundations the advantage by about a factor of 10.) In fact, thinking about quantum foundations led David Deutsch to come up with what is pretty much our present concept of universal quantum computation. Yet you basically can't do it in a US physics department without spending much of your time on something else in order to get tenure. This is part of why I'm not just annoyed, but more like outraged, when I read pronouncements like Hawking's about philosophy being dead.

As with Wayne's post on which this thread comments, I thank Matthew Leifer for the link to this thread. Do read the whole thing if you find this topic area at all interesting as there are several other excellent and clearly expressed insights in it.

Myrvold on philosophy of physics and Hawking and Mlodinow

Posted on by

Since Hawking and Mlodinow's book "The Grand Design" (I keeping wanting to type "The Grand Illusion") is from 2010 (the stack of new copies I saw in the Harvard bookstore must have been remainders), there has, of course, been plenty of discussion of the "philosophy is dead" claim in the blogosphere.  Matthew Leifer kindly pointed me to a post by philosopher Wayne Myrvold in which Wayne tries to find what is reasonable in H & M's claim.  "The quest for the sorts of knowledge that Hawking and Mlodinow are talking has passed from people called philosophers to people called scientists, not because one group failed and had to pass on the torch, but because we started calling that quest “science,” rather than philosophy."  This is partly true, and my mention of "natural philosophy" was meant in part to allude to this, but let's look at the questions H&M pose again: "How can we understand the world in which we find ourselves?  How does the universe behave? What is the nature of reality?  Where did all this come from?  Did the universe need a creator?"  Inasmuch as philosophy of science is still a philosophical discipline, and not a part of science itself, the first question is still a major concern of what we call philosophy, even if scientists, obviously, have to address it at least tacitly because understanding the world is part of what they do.  As for the nature of reality, I suppose that depends in part upon what's meant by "the nature of reality".  But again, this is still a major concern of philosophy, even, perhaps especially, when reality is considered in its scientific aspect. What does it mean to say that the entities mentioned in scientific theories are real, when the theories they appear in get replaced by other theories, in which sometimes the old entities don't appear? It may be that physics will henceforth proveable to handle such questions with litle input from philosophers, but I don't think this is guaranteed. Inasmuch as science addresses the other two questions, about "where it all came from" and the existence of a creator, I also suspect that the broad point of view, and experience in the subtleties of the relevant concepts, of "analytic" philosophy, is still a valuable complement to science.  And then there are all the other questions that philosophy addresses.

Later, Myrvold says:

My own work consists, in part, of addressing the question, “What is the empirical success of quantum theory telling us about the world?”  This is a question that physicists don’t have to ask.  Much of the work done by physicists can proceed without an answer to this question.  Moreover, a case can be made, I think, that there have been moments in the development of quantum mechanics when progress was made by setting aside this question, at least temporarily.  But they can ask this question, and many of them do.  When they do so, they are engaged in philosophy of physics.

I guess physicists don't have to ask this, but many of them do. Plenty of scientists, in fact, think science is about finding out how the world is, beyond mere "empirical success". How "the way the world is" relates to "empirical success" is of course a classic philosophical question. But I think that often, when philosophers work on the question of what quantum theory tells us about the world, they are doing physics. This doesn't necessarily imply that Wayne is wrong that the physicists who ask that question are doing philosophy of physics. I take it rather to imply that this is where the unity of human thought that is suggested by terminology like calling science "natural philosophy" is evident. As I said in my first post on this subject, the people currently called "philosophers" have something to contribute, along with those called "physicists" and, perhaps especially, those who don't necessarily care what they are called.

I should point out that Wayne has a lot of good stuff to say following the paragraph I quoted, and I recommend reading it. (That's not to say I agree with all of it, of course.)

Philosophy is alive and well, whatever Hawking and Mlodinow may think.

Posted on by

Browsing in the Harvard Bookstore in Cambridge, MA last week, I looked at the first chapter of Stephen Hawking and Leonard Mlodinow's 2010 book "The Grand Design".  I was hit by this:

How can we understand the world in which we find ourselves?  How does the universe behave? What is the nature of reality?  Where did all this come from?  Did the universe need a creator? ...

Traditionally these are questions for philosophy, but philosophy is dead.  Philosophy has not kept up with modern developments in science, particularly physics.  Scientists have become the bearers of the torch of discovery in our quest for knowledge...

It's not only wrong, but even, I think, a bit arrogant to dismiss philosophy as dead.  Have these guys even read any contemporary philosophy of science, or mind? Have they been to any conferences on the philosophy of physics recently, like maybe New Directions in the Foundations of Physics?  Have they read Oxford philosopher David Wallace's recent work on the "many-worlds" interpretation of quantum theory which, although I'm quite out of sympathy with it, I think is genuine progress in understanding how one might make sense of --- and what are the obstacles to making sense of --- this view of quantum theory, which is subscribed to by some though certainly not all practicing physicists and cosmologists?   For that matter, are they not aware of the close interaction between some philosophers of science and cognitive scientists?  Or the attention that philosophers Paul and Patricia Churchland have paid to neuroscience (not that I agree with their views)?

So that's one point, that philosophy is hardly ignoring science.  I argue below (and the Wallace example already provides some evidence) that it has useful contributions to make to those parts of physics that deal with the kinds of big questions Hawking and Mlodinow raise.  But one other point needs to be made, which is that philosophy has much broader concerns, involving politics, morals, the good life, aesthetics, and social science, and in these areas too, it is alive and well and contributing.  I sincerely hope Hawking and Mlodinow don't think science is "the torch-bearer" there too, because although of course it is not irrelevant even there (probably no part of human thought can be declared a priori completely irrelevant to any other) that is a torch it is not capable of bearing.  If they really do think science is the torch-bearer here, I think they are contributing to the stunting of serious thought in these areas that are just as important to humanity as science, and indeed, to a stunted conception of humanity.

Now, I can dig that Hawking and Mlodinow, if they were to attend New Directions, might think that some of the stuff being done is not of interest.  In particular there is usually not that much philosophical discussion around string theory and M-theory, although quantum cosmology does come up on occasion.  Maybe they are not interested in the quantum foundations issues like "is the quantum state epistemic?" that come up frequently in New Directions.  I wouldn't be surprised, though, if there are other philosophy conferences that I don't attend where M-theory and quantum cosmology get much more attention.  Maybe they might think some of the stuff aimed at understanding the conceptual content of physical theories like general relativity that have been around for about 3/4 of a century, and comparing them to older theories like Newton's and heck maybe even Aristotle's, is pointless.  I'm referring to James Weatherall's excellent talk "Explaining intertial motion and the foundations of classical space-time theories".  (Here's a link to the paper the talk is based on.) But I'm speculating here; maybe they'd love it, realize that it's worth thinking about the conceptual structure of existing theories as one tries to incorporate what was good about them and go beyond (combining classical general relativistic space-time theory with quantum theory).  Or maybe they'd think it was all understood by physicists long ago, so while not pointless, just not contributing to progress.

Here's yet another point.  I frequently read or hear physicists spouting some methodological priniciple they got from some philosopher of science, often Karl Popper, or some view that is common in some branch of science but considered by philosophers to be quite problematic.  Sometimes it is used to good effect, sometimes used in a quite unsophisticated manner, with little consciousness of drawbacks and caveats well-known to philosophers.  For instance, some physicists freely use the frequency interpretation of probability with little or no understanding of its serious difficulties.  I have heard one of the world's most renowned cosmologists do this, and in response to my objections, dismiss the "Bayesian personalist" (sometimes called "subjective") view of probability by saying something along the lines of  "I'm not interested in betting, I'm interested in describing the world"), although I have also found that other reknowned cosmologists do have an active interest in the "personalist" interpretation of probabilty.  I suspect there are plenty of other places where, when physicists start addressing questions formerly thought of as "philosophical", or when they use philosophical principles or positions in formulating their physical theories (or their "interpretations" of such theories, which one might argue are really an essential part of the theories themselves), philosophers can help physicists avoid making both elementary and subtle philosophical (or perhaps we should just say conceptual) mistakes.

I have no problem with the view that the questions posed by Hawking and Mlodinow in the above quote are not just the province of philosophy, but require input from what used to be called "natural philosophy": science, including physics.  Nor do most contemporary philosophers!  But some of the careful conceptual analysis that philosophers have done, over the course of the twentieth century, of notions like truth, confirmation, induction, falsification, refutation, meaning, reality, perception, observation, theories, and so forth, is enormously relevant to any attempt to say what current physical theories, and speculations like M-theory, really mean for "the nature of physical reality".  It is cool that Hawking and Mlodinow are engaging in this attempt, and I plan to get their book out of the library and see what they have to say.  Perhaps I will even end up thinking that they have made enormous progress.  But I think they are foolish to dismiss the potential for contribution by philosophy to this enterprise.  Indeed, in their description on pages 6 and 7 of their philosophical approach, they say plenty of things that are easily found in the "analytic" philosophy of the latter part of the 20th century:  for example "we shall adopt an approach we call model-dependent realism.  it is based on the idea that our brains interpret the input from our sensory organs by making a model of the world.  When such a model is successful at explaining events, we tend to attribute to it, and to the elements and concepts that constitute it, the quality of reality or absolute truth.  But there may be different ways in which one could model the same physical situation, with each employing different fundamental elements and concepts.  If two such physical theories or models accurately predict the same events, one cannot be said to be more real than the other; rather, we are free to use whichever model is most convenient."  Well, philosophers have been discussing this possibility for decades.  Most usually, it is called "the underdetermination of theory by evidence." So, probably, have physicists; I am not sure in which community the possibility was first mooted, or whether it has occurred many times independently.  I'm looking forward to seeing what use Hawking and Mlodinow make of this possibility, but I consider it a strong possibility that the philosophers who have thought about it carefully may have something useful---useful to physics---to say about its use in physics, or in the application of physics to the big questions Hawking and Mlodinow aim to address.

Okay, enough rant.  I want physicists to think about the big questions; I hope Hawking and Mlodinow have genuine insight on them.  I'll report on that as I read their book.  But I really, really think it is miguided to dismiss the possibility that the field of philosophy as currently practiced has anything to contribute here.   And it goes beyond misguided to downright pernicious, and perhaps to a kind of narrow-minded science triumphalism which is, frankly, morally dangerous, to claim that "philosophy is dead" and that science is bearing its torch.  Let's hope that philosophers and physicsts continue to join forces where appropriate, as we do at New Directions, and indeed that they expand cooperative efforts, to deal with the big questions Hawking and Mlodinow want to address, to deal with other big questions, to deal with issues of how physics might best progress, how the insights of quantum theory and general relativistic spacetime theory can be combined into a more unified physical theory, and to understand better how physics and science fit into the broader picture of rational, and irrational, human activity.

Tim Maudlin on the training of physicists, the evolution of intelligence, and more

Posted on by

I had to link this interview with philosopher Tim Maudlin, in the Atlantic, when I read his observation that "The asking of fundamental physical questions is just not part of the training of a physicist anymore." But there's a lot more of interest in the interview as well. I found the article via Andrew Sullivan's blog; Sullivan found Tim's thoughts on the evolution of intelligence to be particularly interesting:

What people haven't seemed to notice is that on earth, of all the billions of species that have evolved, only one has developed intelligence to the level of producing technology. Which means that kind of intelligence is really not very useful. It's not actually, in the general case, of much evolutionary value. We tend to think, because we love to think of ourselves, human beings, as the top of the evolutionary ladder, that the intelligence we have, that makes us human beings, is the thing that all of evolution is striving toward. But what we know is that that's not true. Obviously it doesn't matter that much if you're a beetle, that you be really smart. If it were, evolution would have produced much more intelligent beetles. We have no empirical data to suggest that there's a high probability that evolution on another planet would lead to technological intelligence. There is just too much we don't know.

Indeed there is, but it points out some very interesting questions: is there a tendency, given enough time, for a species intelligent enough to produce technology to arise on an earth-like planet? Is there, perhaps, a tendency for it to inhibit the evolution of other such species? My personal guess (and it's just that, a guess, not supported by careful thought) is that there is such a tendency, but it takes a lot of time, it builds on, and is part of, a slow increase in the complexity of the most complex organisms. This is, of course, probably the "knee-jerk" view. Whether it inhibits the evolution of other species is something I'm less willing to speculate on (though if Neanderthals were another such species, we may have some evidence (one case!) for inhibition of the branching of a potentially technologically-capable intelligent species into two such species). Whether vertebrates have characteristics making it more likely for them to evolve technologically-capable intelligence than it is for, say, insects to evolve it is another interesting question.

Print-On-Demand publishing: will it allow academics to compete with major publishers?

Posted on by

Since I'm thinking of writing a scholarly book or two, I wonder whether print-on-demand publishing houses, combined with outlets like Amazon, allow academics to effectively compete directly with the more usual academic publishers like Springer, Cambridge UP, Oxford UP, etc...?  I've recently noticed that in ordering new books from all three of these publishers, I've frequently been sent what look like print-on-demand editions.  Here's a bit on Springer's POD activities.   To take one recent purchase, Faraut and Koranyi's Analysis on Symmetric Cones, Oxford, is now print-on-demand, and they're still charging $200 for it.  It's adequate, but much less attractive than the original edition which has the trademark Oxford deep-blue cloth-covered boards, with nicely finished paper (perhaps excessively sized, even) and extremely crisp type.  The print-on-demand edition is on paper that's not as nice, an almost inkjet-printed appearance where the edges of the characters are just not crisp enough for my taste, and the boards are thick, covered with something glossy, and more prone to warp outward so the book doesn't quite close firmly.  Springer and Cambridge POD books are similar.  It's a little more like you LaTeX'd something, printed it out two-pages-to-a-sheet, cut the sheets in half and glued them into a binding.  (Except maybe your average laser printer would produce sharper results---I'd need to do a direct comparison.)  This is quite serviceable for the right price, for usable math books, but $200 (I was able to find it for less, but still an outrageously high price) seems ridiculous.  But if academics were able to publish their works this way, sell for $40-65, deduct the cost of printing (about which I'm quite curious), do a little yearly accounting and extra business at tax time, and pocket the rest, it might be a much better deal than publishing through a major house.  I suspect that for a good academic work, reputation developed through citations and online access (one could make the book available chapter-by-chaper for free, if desired) might work almost as well as the publicity provided by an academic or corporate publisher.  The major issue might be library purchases, I'm guessing.  Anybody out there have any experience or ideas with this?

More info:  Amazon's POD printing and distribution unit, Createspace (Springer's US partner) has an expanded distribution plan claimed to wholesale books to libraries and bookstores.  Cambridge has partnered with LightningSource.

Here's a video of the Espresso Book Machine, for producing paperback books at or near the point of sale, in action:

Here's Amazon's "Pro Plan" at their CreateSpace. The combination of the terminology "royalties" for the money you get, and "self-publishing", seems, technically, contradictory.   Royalties are paid by a publisher for the right to publish and sell your book; if you were actually self-publishing, you would be hiring Amazon/Createspace to print your book, and do some of its distribution and sales, but what you keep would be profit, not royalties.  So I'm curious which it actually is, in their case.  Anyway, you seem to get about 43% of the list price on sales through Amazon, 23% on their Expanded Distribution Channel (to libraries, bookstores, and "certified resellers" at, presumably, wholesale prices, although maybe not since Amazon labels the entire difference between your share and list price "Our Share"), and 63% through something called an eStore (which is presumably an outlet at your own website, linked to Amazon; more investigation warranted).   Those are on a $16 book; on a $45, 320 page book with black and white interior, it looks like 30% through the EDC, 50% through Amazon, and 70% through your eStore.  I'm guessing this is for a paperback.

So, quite a bit better than the standard academic press royalty which I believe is something like 7% or so, but still, through the expanded distribution channel, not that hefty.

How does one prove that domains of positivity of symmetric nondegenerate bilinear forms are self-dual cones?

Posted on by

On mathoverflow, I've asked how one proves that domains of positivity of symmetric nondegenerate bilinear forms on real vector spaces are self-dual cones.  A bilinear form on a real vector space is just a map that is linear in each argument.  (In other words, if you fix , the function that takes to is linear, and similarly if you fix the other argument.)  It's called nondegenerate if the only such that for all , is .  And, of course, it's symmetric if for all , .

A closed domain of positivity of such a form is a maximal set such that .  Maximal means maximal in the ordering of sets by containment, i.e. is not contained in any other set satisfying .  This notion was introduced, or at least used, by Max Koecher in the late 1950s, in work that led to the celebrated result, published in 1958 in "The Geodesics of Domains of Positivity"  (well, actually, "Die Geodatische von Positivitatsbereichen" (Mathematische Annalen 135 (1958), pp. 192--202)), that homogeneous self-dual cones in finite dimension are precisely the cones of squares in finite-dimensional formally real (aka Euclidean) Jordan algebras.  Indeed, probably the very interpretation of the main result of that paper as concerning homogeneous self-dual cones relies on the identification of domains of positivity with self-dual cones that I'm looking for a proof of.

If the form were positive semidefinite, i.e. for all (which implies symmetry) then a domain of positivity for would clearly  be a self-dual cone.  This is practically the definition of a self-dual cone.  The dual of a cone in a real inner product space is the set of all vectors whose inner product with everything in the cone is nonnegative---and the definition of an inner product on a real vector space is that it's a nondegenerate positive semidefinite bilinear form.  A self-dual cone is one that's equal to its dual cone.

For our definition of domain of positivity, the form was required only to be symmetric, not necessarily also positive semidefinite.  Nevertheless, according to things I've read, its domains of positivity are self-dual cones.   These domains are not necessarily unique, of course, although they are maximal, i.e. no one of them contains another).  Although I have a vague recollection of having seen a proof that they are self-dual, I haven't been able to find the paper or come up with a proof.

It's easy to prove that such a domain is a pointed, convex, closed cone.  A natural way to prove that it is a self-dual cone would be to exhibit a positive semidefinite form , depending on and possibly also on , such that is a domain of positivity of .   An idea for how to do this involves the fact that such a form can be diagonalized: we can find a basis for the vector space such that the matrix with elements is diagonal, with diagonal elements .  The number of signs on the diagonal is the signature of the form.  A natural candidate for is the Euclidean inner product in the basis (i.e are the components of in this basis).  That is, we just change the 's to 's in the diagonal form of .

Nondegenerate symmetric bilinear forms are interesting for a variety of reasons.  One of them is that they are closely related to the metric structure on a pseudo-Riemannian manifold.  Something like the following is true: you specify such a form at each point of the manifold, in such a way that the forms at the various points are nicely related to each other, and you've specified the geometric structure of a pseudo-Riemannian manifold.  (One restriction here, I believe, is that the signature of the forms has to be the same everywhere; the forms also need to vary somewhat smoothly, in a manner I should look up and summarize, but not now.)  For example, in the general relativistic description of spacetime, the spacetime manifold has signature .  Or ; people use different conventions.  I'm attracted to , because the odd-one-out corresponds in relativity theory to time, and this way, the forward and backward light cones are the (only!) domains of positivity for the form.  I.e. the form is ; we have (here , etc...).  Interestingly, with the other choice of signature, the domains of positivity consist of spacelike vectors, and there is a continuum of them.  To get a picture of what's going on, consider one time and two space dimensions, with signature .  You can visualize this in , with the vertical axis as time (associated with the diagonal element of the form) and the horizontal planes for constant time as a spacelike plane.  If you rotate the 45 degree line between and say the axis, around the axis, you get the boundary of a double cone, the forward and backward light cones.  But similar cones pointing along any ray in the plane are clearly domains of positivity for the form.  I suspect lots of other cones---basically, any self-dual cone you can fit into the "conic doughnut" that is the closed complement of the double light-cone, i.e. into the spacelike (and null) vectors, are also domains of positivity for this form.

My main reason for interest in the problem isn't pseudo-Riemannian geometry, however.  More on the main reason later.  (It has to do with the Koecher result cited above).

If you found this problem first on mathoverflow, and you have the answer, please post your answer there, and link to it here if you feel like it; if you encountered it first here, please post the answer here indicating you encountered the problem here, and it would be nice if you'd also post it on mathoverflow indicating you found it on my blog.  We can have a little race between we happy few who read this blog, and the overflowing mathematicians.  I know who I'm betting on---your mission, readers, should you choose to accept it, and should any of you actually exist, is to prove me wrong!

(Thanks to Will Jagy, of MSRI, for noticing that I defined nondegeneracy wrong here at first: as requiring that the only for which is . This wrong definition, corrected above, of course says that the form has no nontrivial "isotropic" or "null" vectors (ones for which ). And we certainly don't want to assume that! Sorry about the slip-up, which I dont think affected anything else in the post.)

Pablo Arrighi: Unitarity plus Causality implies Locality

Posted on by

Pablo Arrighi of the University of Grenoble spoke on his result, with collaborators Vincent Nesme and Reinhard Werner (both now at the Leibniz University Hannover), that  Unitarity plus Causality implies Locality, at the PiQuDos seminar today at Perimeter.  I heard him speak on this result over a year ago at Foundational Structures for Quantum Information and Computation at Obergurgl, Austria;  I thought it was one of the standout talks of the workshop, and his talk today, which also covered more recent work along the same lines, reminded me how interesting I'd found his result when I first heard it.

Arrighi, Nesme, and Werner consider a quantum system associated with a graph having a countably infinite number of vertices, and an arbitrary edge structure.  At each vertex is a quantum system, finite or infinite dimensional, represented by a Hilbert space.  The edge structure is supposed to represent some notion of two systems being "nearby", so that it's physically reasonable for them to influence each other during one step of time evolution.  Roughly speaking, this is their notion of "causality" of a time evolution: that only such nearby systems have any influence on each other.  They define a Hilbert space associated with this infinite set of quantum systems.  It's not quite the tensor product of this infinite set of Hilbert spaces (which would not necessarily be a Hilbert space), but rather the span of all "finitely supported configurations", i.e. product states having a special state on all but a finite number of systems.  (You can do things -algebraically and do better, Pablo said, but this should be good enough.)  Their main result states, roughly speaking, that if a unitary evolution satisfies "causality", it can be represented as a circuit of quantum operators each acting on a neighborhood (a vertex and its neighbors) in the graph; the circuit has depth no greater than the square of the degree of the graph, plus 2.  (The degree of the graph is the largest number of edges emanating from a vertex.  For example, in lattices that repeat a hypercube of some dimension as their basic structure, the degree is twice the dimension).  In other words, there is a representation via "local"---although multi-way---interactions, happening in parallel on disjoint neighborhoods.  It may be necessary to take several successive rounds of interactions, happening on different sets of neigborhoods, but it's never necessary to take more than the degree squared plus two rounds.  So in a "spatial" hypercubic lattice in N dimensions, you never need more than 4N^2+2 rounds of interactions of interactions with neighbors.  (True, these are 2N+1-body interactions.)

I still haven't finished saying what the result is, because I didn't yet say (except roughly at the beginning) what the assumption of causality is.  It's that the state of the quantum system at a vertex after the overall unitary evolution U on the entire (infinite!) graph, depends only on the state of its neighbors before the evolution.  By state, he means reduced density matrix, after the other systems are traced out.  (Equivalently, in the Heisenberg picture we could say that an operator "supported only at site x", i.e. of the form "A at site x tensor the identity everywhere else", has, when evolved with , support only at the neigborhood of x, i.e., is of the form "Something on the tensor product of x's neighborhood, tensored with the identity everyplace else".)

Now, given that causality is defined by the influence of a state at a node in the graph propagating only to nearest neighbors (and the node itself) during the unitary evolution, it's perhaps not so surprising that it has a representation in terms of interactions among neighbors.  The important thing to remember, though, is that the causality condition concerns all the overlapping neighborhoods in the graph simultaneously, while the circuit-local representation involves only nonoverlapping neighborhoods, interacting in parallel, in each layer of the circuit, and bounds the number of layers as described above.

Actually, what I've described is a corollary to the main theorem, since this corollary has more immediate intuitive import.  I'll leave you to follow the link to the paper at the beginning of this post, if you want to see the details of the theorem as well.  Also, I've talked as if an edge between two nodes means that either node can influence the other during the evolution; actually, the authors allow for directed graphs, so that (x,y) maybe be an edge in the graph without (y,x) also being one;  the notions of causality and locality are then adjusted to refer to the graph and its transpose (i.e. the one specified by transposing its adjacency matrix) appropriately.  Here, a directed edge (x,y) in the graph means site x can influence site y in one step of unitary evolution;  (y,x) means y can influence x, and it's possible in their framework to allow influence in one direction but not the other, if desired.

One more thing, though: for those who think that this is too obvious, according to Pablo the analogous theorem probably doesn't hold if unitaries are replaced by completely positive maps.  He also thinks there is not a direct analogue even for classical stochastic evolution.  The development of an appealing strengthening of Causality that would allow a similar representation theorem for completely positive maps is something he's actively working on.

The talk also covered some related work that's more recent, such as cool results about the notion of "intriniscally universal" quantum cellular automata on certain kinds of graphs.  These things can simulate the action of any other cellular automaton by means of a short encoding, which takes the state of each cell in the simulated automaton to an encoded state on a block of adjacent cells in the graph of the universal automaton;  several steps---say, steps---of the universal automaton then simulate the action of the simulated automaton, on the encoded state.  After steps of the universal automaton, one can apply the inverse of the encoding map, to obtain the state that would have been obtained under steps of the simulated automaton.   A paper (with Jonathan Grattage)   is here.

The talk should soon be available at PIRSA.

QIP=PSPACE for the layperson I: Complexity Classes and Polynomial Time

Posted on by

Next time you're at a party and someone asks "hey, did you hear that Britney Spears was seen with the lead actor from Desperate Housewives at an L.A. disco last week?", try replying "No, but did you hear that Rahul Jain, Zhengfeng Ji, Sarvagya Uphadyay, and John Watrous showed that QIP=PSPACE in July?  This is likely to be a foolproof way of ensuring you don't get invited to any parties hosted by your interlocutor, which is likely to be a good thing.  If, however, your conversation partner is thinking fast enough to  reply, "No, so give me the skinny on it," you're going to want to be prepared.  Luckily it's not all that hard.  This is the first in a series of posts that will enable you to answer such a comeback in detail, captivating entire the party for at least a short while, and clearing your social schedule for months to come, as well as leaving you free in the moderately near-term to enjoy whatever remains of the Sutter Home Pink Zinfandel at the drinks table.  John Watrous gave an excellent colloquium at the IQC (Institute for Quantum Computing) yesterday, on the above-referenced work showing the the complexity classes QIP and PSPACE are identical. I originally imagined writing a fairly technical post aimed at colleagues; they will probably want to skip to number II or maybe even III; this post sets the stage for defining the complexity classes QIP and PSPACE, by reviewing the notion of complexity classes.

Complexity classes are, roughly speaking, sets (although I imagine the term "class" is used instead of "set" advisedly, for the set-theory-minded among you---perhaps I will come back to this) of computational problems.  Normally, they are taken to be classes of decision problems: problems of the form:  given an input from a set of possible inputs (the specification of this set is part of the specification of a particular computational problem), decide whether it has, or does not have, a certain property.  To say that a computer program solves such a problem is to say that it outputs "0" if the input doesn't have the property, and "1" if it does.  Normally, the set of possible inputs to a computational problem is taken to be countably infinite (like, for instance, the integers, or the set of finite-length strings of 0's or 1's ("binary strings"), or the set of ASCII text strings...).  So, an example of a problem would be "take a finite string of 0s and 1s; is the number of 1s odd?"  This problem is called PARITY, since evenness or oddness is a property known as the "parity" of a number.  Another example, often called OR, also involves binary strings as inputs; it asks, "is there a 1 in the string"?  Determining whether an integer is prime or not is another example; where the inputs are now integers instead of binary strings.  (But they can be coded, and often are coded, as binary strings---that is, they are written in their base-2 expansion.)  A problem that takes pairs of integers, instead of single integers, as inputs is to determine whether one integer divides another.  There are also more complicated problems, in which the output is not "0" or "1", but is drawn from a larger set of possibilities, but we won't discuss them much here.  An example would be: given an integer, tell us whether or not it is prime and if it isn't, exhibit a nontrivial factorization of it.

Not just any class of decision problems is a complexity class, although I haven't seen (nor do I expect to see) a formal definition of "complexity class", or even much in the way of necessary conditions for being a complexity class.  A complexity class is supposed to reflect something about how hard it is to solve a decision problem, and is often described as "the set of all problems that can be solved by computations of *this sort*", where "this sort" describes some model of how one might do computations.  The model is often quite zany compared to how we actually compute things, but it's rigorously specified.

Now, a computational decision problem, as we've defined it, in most cases clearly can't be "solved" once and for all by a computer.  It involves a countably infinite set of possible inputs, and so the "full solution" would involve listing, for each of these inputs, whether the answer is "0" or "1".  This answer would take an infinite amount of space (and presumably an infinite amount of time, given a lower bound on the amount of time it takes to write a character) just to write down.  So if we want to relate problems like this to reasonable notions of computation, we need to discuss programs that give the right answer for whatever input is presented.  To say things about how hard the problem is is not to say how hard it is to write down all the answers, but rather we need a notion of how hard it is to do the computation on an input.  What's often done is to study how the resources required---the number of computational steps, and the amount of computer memory needed---scale with the size of the input.  This means, of course, that we need not just a countable set of inputs, but one equipped with a notion of size.  In the case of binary strings, the length of the string is what's used.  This works for numbers, too---we just use the number of bits in the binary expansion.  (Up to a constant factor, this is the same as the number of digits in its decimal expansion.)  This is why you may need to choose things like "128-bit RSA key" versus "256-bit RSA key" when doing secure internet transactions, for example:  the security of these transactions is based on the idea that it's hard to factor integers, and what "hard" means here is roughly that the amount of computational resources needed to factor grows faster than any polynomial, with the number N of bits in the binary expansion of the number.  If I remember correctly, the worst-case resources for factoring an N-bit number using the best currently known algorithms scale as around , i.e. they are (up to a proportionality constant C) exponential in the cube root of the number of bits.  More needs to be said, of course---not every N-bit number will take this long to factor, but for large enough N, some numbers will take this long.  For cryptographic security, it's actually important to use a procedure for choosing key that is overwhelmingly likely to pick such hard instances---multiplying together large enough primes is, I guess, thought to work.  This is, of course, a side issue:  the main point is that the definitions of complexity classes often contain reference to how the resources used by a program that solves a decision in problem in the class, in a particular model of computation, scale with the size of the input.  The very important complexity class P, for polynomial time, is roughly the class of decision problems for which there's a polynomial Q (the polynomial may depend on the problem) that gives an upper bound to the time that it takes to solve the problem in a standard computational model closely related to actual computers, namely the Turing machine model (or any model polynomially equivalent to this, such as the -calculus introduced by Alonzo Church at around the same time Turing introduced the Turing machine).  That is, if is the length of input , the time it takes a Turing machine to solve the problem on input is no greater than .

The notion of polynomial time computation is important in the definition of many other complexity classes, and it's also the complexity class that's perhaps the most reasonable candidate for a class of "efficiently solvable" decision problems.  In actual practice, of course, we often solve smallish instances---or expend huge amounts of resources to solve moderate-sized instances---of problems from harder complexity classes;  and occasionally, we have polynomial algorithms for problems for which we'd like to solve large instances, but can't because the degree of the polynomial is too high.  If you hang out with cell-phone security folks, for instance, you'll find that encoding and decoding of messages that is linear in key length is considered a huge advantage compared to quadratic in the key length; forget about higher degree.  Here the small size of cell-phone processors is important.  But degree of a polynomial---and even, sometimes, the constant out front---can be important for big machines, too.  The ellipsoids methods for linear and semidefinite programming, although polynomial, has seen little practical use; interior-point methods, also polynomial, revolutionized the field as they perform much better in practice.  (I'm ashamed to say I don't know offhand if it's the constant or the degree that's mostly responsible for this.)  Actually, for LP the simplex method, which is worst-case exponential, is still in wide use because it performs just fine on most instances---the hard ones appear to be rare and bizarre.  But despite these caveats, P is an important complexity class, with a definite relevance to the line between what it's practical to compute and what it's not.

In the next instalment, I'll cover the classes IP, QIP, and PSPACE---classes that, it's pretty clear, go far beyond what it's practical to compute, but which are fun to think about nonetheless.  (I presume they have more scientific relevance than just being fun; perhaps we can be enlightened about that in the comments.)