 OK, I just had to copycat this link. Via the Quantum Pontiff, Universe Splitter, a supposed new app for the iphone that supposedly hooks up to a quantum randomness generator, allowing you to condition your decisions on quantum randomness and ensure---if you believe in the Everett interpretation of quantum mechanics---that you can "have your cake and eat it too. I hope this thing's for real, but unless it's just my lack of App savvy, Apple may not be buying the Everett interpretation.
OK, I just had to copycat this link. Via the Quantum Pontiff, Universe Splitter, a supposed new app for the iphone that supposedly hooks up to a quantum randomness generator, allowing you to condition your decisions on quantum randomness and ensure---if you believe in the Everett interpretation of quantum mechanics---that you can "have your cake and eat it too. I hope this thing's for real, but unless it's just my lack of App savvy, Apple may not be buying the Everett interpretation.
Category Archives: Physics
Gross, Mueller, Colbeck, and Dahlsten: "All reversible dynamics in maximally non-local theories are trivial"
David Gross, Markus Mueller, Roger Colbeck, and Oscar Dahlsten have considered the "maximal non-signaling tensor product" of "boxlets", and shown that the reversible dynamics of this state space consists just of permutations of the systems (the boxlets) followed by reversible local transformations (i.e., ones on the individual boxlets).
What the heck does that mean, you ask? Well, "boxlets" were introduced in several contexts. In the "operational quantum logic" literature they're sometimes called "semiclassical test spaces". In quantum foundations and informations, they were introduced as a generalization of a notion of Popescu and Rohrlich, who introduced the two-measurement, two-outcome-per-measurement boxlet in order to describe correlations between measurement results on distinct systems that can be stronger than quantum correlations, but still don't allow someone ("Alice") in possession of one of the systems to signal to the other ("Bob") just by making measurements on her system.
A "boxlet" is a system on which there are M distinct alternative measurements one can make, each with K outcomes. (More complex versions allow different measurements to have different numbers of outcomes.) The allowable states of a boxlet are given by specifying M probability distributions, each one over K alternatives: for each measurement, the probabilities of each of its K outcomes. All possible lists of M such distributions are allowed; this is a convex, compact subset of an MK dimensional vector space (one dimension for each probability). The M normalization constraints mean that this set lies in an MK-M (i.e., M(K-1)) dimensional affine subspace (higher dimensional generalization of the line, plane, etc... of high-school geometry). The possible states of a pair of such systems are given by the "maximal tensor product" of a pair of these compact convex state spaces. The technical definition of maximal tensor product of state spaces can be found here. Another way of defining this is that it's the state space of the Foulis-Randall tensor product of the "test spaces" (definitions reviewed in Sections II and IV of this paper) describing each of the boxlets. A test space is just a collection of subsets of some set; the elements of the set interpreted as measurement outcomes, and the subsets, called "tests", as measurements. The semiclassical test space of a boxlet like the ones I described above just consists of a set of MK elements, partitioned into M sets of K elements. A state on a (finite, like the ones in question) test space is a function from the set to the real numbers between zero and 1, i.e. to probabilities, such that for each test, the probabilities of the elements of the test add up to one. The Foulis-Randall tensor product of two test spaces just takes their Cartesian product, and allows any probability assignments such that the "marginal states" obtained by fixing a measurement on one side and marginalizing all the joint distributions of this fixed measurement with measurements on the other side, is independent of which measurement is marginalized over. That is, Alice can't signal to Bob (by affecting the probabilities of the outcomes of one or more of his measurements) just by her choice of measurement.
Now, a transformation of the state space is an affine map from the state space to itself (i.e. one that preserves convex combination, which seems only reasonable), and a reversible one is one that has an inverse that is also an affine map of the state space. So what GMCD are saying is that, if you combine boxlets this way, there are no very interesting reversible dynamics: just combinations of local reversible dynamics on the individual boxlets, and permuting the boxes amongst themselves.
An interesting question is, can one extend this result to maximal tensor products of *arbitrary* systems with convex state space (locally equipped, let's say, with the maximal set of possible effects)?
See the comments on the Information Causality thread at Dave Bacon's blog for a bit more discussion (and related interesting matters).
Tension detected!!! Worldview manager analyzes my views on quantum mechanics
Scott Aaronson has gotten a couple of students to help him realize Worldview Manager, which asks you to indicate a level of agreement or disagreement with various statements on a topic, and then detects "tension", i.e. something akin to inconsistency, between your responses. No significant tension was found in my views on quantum computing, but on quantum mechanics (mostly fairly foundational questions), here's what the thing came up with:
"Tension detected!
You indicated
- Disagreement with the statement "There is a single wave function for the universe, which has been evolving unitarily since the big bang."
- Agreement with the statement "There is no faster-than-light communication."
It would seem that this is logically inconsistent. Please consider modifying your responses. If you do not want to resolve this tension now, you can defer it until later.
If you are confused as to why this represents a logical inconsistency, you can read our explanation."
I did, although you could more properly say I was being too lazy to even be confused... As a not entirely irrelevant side note, I only indicated 20% agreement (via a slider scale with no numbers attached, though) with the "no faster-than-light communication" statement (and 80% disagreement with the other).
"Here is a brief explanation as to why your answer selection represents a logical inconsistency.
Let
* A be the statement:
There is no faster-than-light communication.
* B be the statement:
There is a single wave function for the universe, which has been evolving unitarily since the big bang.
* C be the statement:
The collapse of the wave function (i.e., measurement) is a real physical process, not explainable in terms of unitary evolution.
Then A implies B as follows:
* One of C or B because
If there's no collapse process, then presumably one could in principle write down a wavefunction for the entire universe.
* C implies not A because
If collapse is a real physical process, then it requires a form of faster-than-lightsignalling when applied to entangled states."
I guess I don't yet agree with the "presumably" above, and so not with "One of C or B". I don't believe "there's no collapse process", just that it's not a "physical process". On the view I lean toward, the wavefunction is probably not a "real physical entity", it is a tool we are using to help understand and predict the behavior of systems, so the fact that its collapse isn't a physical process doesn't imply that there's no collapse.
Time for some coffee. Am I missing something?
Just for the record, my full answers so far:
| Quantum Computing | ||
| The Threshold Theorem provides a convincing demonstration that, because of the linearity of quantum mechanics, it is possible in principle to correct errors in a quantum computer faster than they occur. | 80% Agreement | |
| It is possible to simulate any quantum system on a classical computer in polynomial time (i.e., exponentially faaster than the "naïve" method of writing down the entire wavefunction). | 80% Disagreement | |
| Quantum mechanics as described in standard physics textbooks is an accurate framework for all of physics. | 40% Disagreement | |
| If quantum mechanics as described in standard physics textbooks is true, then it is possible in principle to build a scalable quantum computer. | 90% Agreement | |
| Any quantum computer will inevitably be subject to noise and decoherence that will prevent it from exponentially outperforming a classical computer. | 80% Disagreement | |
| A fast classical algorithm for factoring integers will eventually be discovered. | 20% Disagreement | |
| The Extended Church-Turing Thesis is false: that is, it is possible in principle to build computers that efficiently solve problems outside the complexity class BPP. | 30% Agreement | |
| A quantum computer is essentially an analog computer, and will fail to scale for the same reasons classical analog computers failed to scale. | 80% Disagreement | |
| Quantum Mechanics | ||
| There is a single wave function for the universe, which has been evolving unitarily since the big bang. | 80% Disagreement | |
| Quantum mechanics is an experimentally successful description of the behavior of microscopic systems. | 90% Agreement | |
| For a physical theory to make sense, it must have some notion of "the past" besides just memories and records in the present. | Completely neutral | |
| There is no faster-than-light communication. | 20% Agreement | |
| Mixed states, as the most general representation of an agent's knowledge of a quantum system, are more fundamental than pure states. | Completely neutral | |
| Quantum mechanics is about our knowledge and information, not directly about ontology (i.e., what really exists). | 30% Agreement | |
| When measuring a quantum state, we have the freedom to choose the measurement basis (for instance, whether we want to measure the position or momentum). | 30% Agreement | |
| The outcome of every quantum measurement is "preordained" from the beginning of the universe. | 50% Disagreement | |
| Quantum mechanics shows that consciousness or observation must play some fundamental role in the laws of physics. | 20% | |
Physics and Song: Perimeter to U2 Tour 360, Rogers Centre, Toronto 9/16/2009, courtesy of Blackberry and/or Mike Lazaridis
Courtesy of Mike Lazaridis (CEO and co-founder of Research in Motion, the company that makes the Blackberry, and founder of Perimeter Institute, where I work), and/or his company (THANKS!!) the staff at Perimeter Institute was bused to Toronto and treated to the first of two U2 shows in the Rogers Centre, downtown next to the CN tower. The roof was open on the arena, and those on the west side could see changing, glowing colors lighting up the elevator strip all the way up the CN tower, and encircling the observation deck. In my account of the concert below, I'll link to mostly YouTube videos to that give a play-by-play record of most of the concert---be warned that some of these are pretty low quality, though a few are surprisingly good.
Overall, the concert rocked. Although I haven't followed U2 closely, I have a couple of their CDs from quite a while back---the excellent Achtung Baby, and a double live one, plus a few LPs kicking around that I haven't listened to recently. They haven't lost their touch. I particularly enjoyed some of the songs from their new album: the opening sequence "Breathe", "Magnificent", and "Get on Your Boots". My notes call the latter "surrealistic hard rock, with fuzz bass and Nirvana-y guitar riffs". Its title and tacky-but-tasty riffs (think snarfing a box of Snyder's of Hanover Honey Mustard & Onion Pretzels) remind me of Sonic Youth's "Dirty Boots". I liked the live "Boots" a bit better than the studio video version you can hear here--- a little grittier and harder-rocking.
Their traveling stage set (apparently one of three---the setup takes long enough that they need to start in one venue before the shows are finished in the next) is a giant pale-green thing, adorned with orange buttons and a tower sticking out the top, that looks like a cross between a giant four-legged beetle and the a lunar lander, and forms a tall canopy over the circular stage. Under the belly of this thing, there's a huge circular video screen made of elongate hexagonal chunks, which can be interpreted as the thrust nozzle of a rocket engine. Half-way through the show, the thing elongates vertically to more than twice its size, revealing that the screens are mounted on diagonally criss-crossing metal rods hinged to each other as in a folding set of coat-pegs, or wash-hanging rack. It's used to show closeups of the performers, and various other graphics integral to the show.
We unfortuately missed the opening act, Snow Patrol, as the bus ride from Waterloo to Toronto is a lengthy proposition when you leave at 4 PM on a weekday. The show started out with the bug thing towering over the empty stage as Bowie's "Space Oddity" was played on the sound system. Then some moody, pretty music as the lights went out, the band came on, and the spots came up on them one by one, segueing into the band playing "Breathe" off their new album (Here's longer, but better, video of the whole initial sequence from the last part of Space Oddity, through the band entrance and "Breathe"). Initially the sound balance left something to be desired---the low bass and kickdrum frequencies that resonate in your chest, and below, were overemphasized for my taste, while the actual low and low-midrange frequencies where the bass melody lives were underemphasized. And the non-kickdrum parts of the drumset, especially at lower frequencies, were a bit undermixed too (partially remedied by Bono's call for "more drums" early in the set). But basically the sound was pretty good, especially for an open arena which is probably pretty hard to fill sonically. Vocals and guitar lines were pretty clear. The band was able to carry things through Breathe and "No Line on the Horizon" as the sound settled down, or I stopped noticing it, and by Get On Your Boots things were rocking just fine. (Here's some good video footage, with crummy no-bass sound, of the CN tower ... not sure this is actually "No Line" as claimed by the tuber who posted it, though.) Here's the beginning of Magnificent (another song I liked from the new album, here's another snippet of it, and here's probably a better video of the whole song, from near the stage.) This was followed by Get on Your Boots---no acceptable video from Toronto, so here it is from the opening show of the tour, in Barcelona's Olympic Stadium. "Beautiful Day" from 2000's "All That You Can't Leave Behind" ended with a little snippet from Elvis Costello's "Alison", though with an somewhat altered, and I thought less interesting, melody. "I Still Haven't Found What I'm Looking For" from Achtung Baby, here beginning with the audience doing a good bit of the singing, was the first of the oldies but goodies for me, followed by a nice version of Elevation (also from "All..."), with the band really getting into a disjointed but rocking groove appropriate to the somewhat "surrealistic" lyrics ("why can't the sun // shoot me from a gun.."). "Your Blue Room" was a classic, lazing-across-inner-space "orbit" song, at a meandering tempo with looping "satellite" motifs and footage shot from the International Space Station, and a little sprechstimme from Commander Frank. Nice touch (as was the LEM-like stage-set) in the anniversary year of the moon landing. (Here it is from Chicago a few days earlier, from farther out so you can see the video display.) [Unknown Caller] Until the End of the World resumes the sequence from Achtung Baby (begun with "Still Haven't Found...") An even better video of End. Stay. Unforgettable Fire (nice sound and video, but cut off after 2:50. ). This is when the rocket nozzle video screen got vertically elongated. More good video of Unforgettable Fire; relatively decent sound for this kind of thing, but bass-challenged. City of Blinding Lights. Vertigo / Pump It Up. Bono announced that Elvis was in the house; this, and the bit of Alison and Oliver's Army, were presumably in his honor. (Some parts of this sound like Dirty Boots as well.) I'll Go Crazy if I Don't Go Crazy Tonight (sound issues), a lightweight but hard-rocking pogo-ey, poppy bit of infectious fluff off the new album. Another version of Crazy with different sound issues and funny audience vocal. Sunday Bloody Sunday (OK sound, long view; late beginning). Ends with a snippet of Elvis Costello's "Oliver's Army". MLK, for Aung San Suu Kyi. Walk On, and One, for Aung San Suu Kyi (seriously bad audience vocals from near whoever recorded this, but with some redeeming value (humor)). Amazing Grace. Where the Streets Have no Name.
Ultraviolet (Light My Way), another oldie but goodie from Achtung Baby. Bono doesn't slack off when covering old songs...the phrasing is different in different performances, his heart and mind is in it. With or Without You. Moment of Surrender.
2005 Winner's Tank Shiraz, Langhorne Creek, Australia... and the Future of Science
I've mentioned before how fantastic the 2005 Aussie Shirazes are, especially from the Barossa valley and McClaren Vale (e.g. The Maverick). Here's a review of the wine that got me started on them, in the form of an email I send to Michael Nielsen a few years back, when I first tasted this wine. The 2006 was also good, but like many of the '06 Australians, less balanced and suave, and a bit thinner and sharper, than the the '05 incarnation. I've added a few links. Maybe soon I'll post more on the '05 and '06 Shirazes from Oz.
Hi Michael---
I opened a wine tonight that in several ways reminded me of you. So I'm suggesting you try a bottle
or six before you depart your native land for the greener (?), but certainly colder (except in the summer when you'll be sweating buckets) pastures of Ontario. It's "The Winner's Tank" 2005 Aussie Shiraz, Langhorne Creek. I was dubious about this puppy because its label is a photo of some big square concrete tank in the middle of pasture, behind a barbed-wire fence, with "Hawks '05" inscribed, along with some shtick about how the local tradition is for the winners of the annual Aussie Rules football tournament to gather in the vineyard and paint their names on the tank.

Clearly just a bunch of hooey from some canny Aussie businessmen-winemakers to sucker some of us ever-gullible yanks into spending twelve bucks on a bottle---to be consumed, no doubt, with the shrimp we've got going on our barbie. But having allowed myself to be suckered into it by a salesman at the Santa Fe Cost Plus---or else at Kokoman, our local Pojoaque-pueblo based purveyor of cheap beer to the masses and expensive Bordeaux to the Santa Fe/Los Alamos crowd--I opened it tonight. Well, it was excellent. Probably shouldn't talk it up too much for that promotes disappointment (it's just wine, for crissake) but, what the heck. One of the better wines I've ever had---starting out kind of velvety, and also fruity but not with the enjoyable but somewhat tacky blueberries-'n-bubble-gum taste of some of the cheaper-but-still-decent Australian shirazes. Nope, this also had a hint of darkness, maybe even veering towards an off-taste, rubbery or rotty but opening out with air into a kind of stony complexity you get with the best Rhone Valley syrahs of France (or one I had from the Santa Barbara area). Of course the 15.5 percent alcohol could be influencing my perceptions too. (But more often it's hard for the flavors to stand up to that alcohol level.)
Anyway, recalling the tasty bottle of Jacob's Creek Cabernet you once bought me for my birthday, or my dissertation submission or wedding or something, and the fact that you're probably the first person I ever heard about Aussie Rules football from, I thought you might enjoy this recommendation, that is if you indulge in wine on occasion.
Sorry I cheesed out on QIP this year... I can't recall if it's because of some confusion about abstract submission and the international date line, or just not getting my paperwork in at LANL with the ever-lengthing lead time required. Possibly I was even doing some research at the time I needed to be paying attention to registration or paperwork. I got into the staying-up-late-at-night-trying-to-prove-stuff mode about extending the no-broadcasting theorem to a general ordered vector spaces context, with Jon Barrett, Matt Leifer, and Alex Wilce (cf. our quant-ph), and kind of let everything else go to hell. It was great, and I have a few other similarly abstract things in the pipeline as a side benefit. I'll bet QIP07 was great too, though.
Anyway, if you run into this wine, try a bottle. You might even stop by your local wine store and see if they have it. If you don't like it, complain to me and I'll reimburse you.
Cheers,
Howard
P.S. By the way, I just saw for the first time your 2004 blog post on effective research and really enjoyed it. It encapsulates some things I've been realizing. (You may see me next writing a book on information-processing in categories of ordered linear spaces, and hoping to reap some dividends in cool theorems along the way.)
I don't think Mike ever tried the wine. There are a lot of Aussie wines, and not all are available everywhere, especially not in Ontario, where I've learned to my chagrin that there is only one source---the Liquor Control Board of Ontario (well, there are some wineries you can buy from, too, but their stuff is well represnted at LCBO). I'm now in Ontario myself---at Perimeter institute, in part to work on the book referred to in the e-mail I quoted; Mike is still in Waterloo, but now instead of working at Perimeter on quantum information, he's writing his next book, The Future of Science, on how the internet will transform scientific research. We invited him to give the after-banquet talk at QIP 2009 in Santa Fe, and I found it inspiring; one of several things that led to me start this blog. For those of you who don't know, here's Michael Nielsen's first book (coauthored with Ike Chuang).
Foundational Questions in the Azores II: Limiting frequency arguments for the Born rule in Many Worlds
To take up where I left off, I was discussing the Many Worlds interpretation of quantum mechanics with Alan Guth at dinner the first night of the FQXi conference in the Azores. If I understood correctly, he seemed to think that the Many Worlds (in the sense of One Hilbert Space---Many Mutually Orthogonal Subspaces in which macroscopically distinct things appear to be happening) interpretation was useful, perhaps needed, to deal with quantum effects in cosmology. I asked him whether he though the question of justifying the Born probability rule in the MWI was an important issue, and whether he had any opinions on it. (The Born rule, introduced by Max Born early in the history of quantum theory, in a famous footnote in a paper of his, it says, rougly speaking, that the probability of finding a given outcome of a quantum measurement is given by the square of the modulus ("absolute value" of a complex number) of the complex component of the state vector in the subspace corresponding to that outcome.) He advocated the Farhi-Gutmann version of an argument going back to James Hartle in 1965, and perhaps earlier to Finkelstein. In his telling, the idea is that as long as one is willing to "neglect components of the wavefunction with vanishingly small modulus", the fact that when one makes 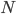 repetitions of the same measurement on the same state
repetitions of the same measurement on the same state 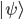 of Hilbert space
of Hilbert space 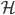 (prepared again for each measurement) the state is represented by a tensor products
(prepared again for each measurement) the state is represented by a tensor products 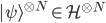 implies that the state is (except for a negligible component) in a subspace in which frequencies are close to those given by the Born rule---approaching the Born frequencies ever more closely as
implies that the state is (except for a negligible component) in a subspace in which frequencies are close to those given by the Born rule---approaching the Born frequencies ever more closely as 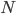 gets larger.
gets larger.
Hopefully I've rendered what Guth had in mind reasonably well---we didn't formalize things on a napkin or anything. In some versions of this argument, one actually goes to an infinite tensor product Hilbert space, and the claim is made that the vector corresponding to an infinite number of independent preparations of 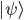 ---call it
---call it 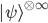 if you like---just is an eigenstate of a "relative frequency operator" on this infinite tensor product Hilbert space, with eigenvalue equal to the Born probabilities. I believe that's the claim of the Farhi and Gutmann paper --- but Caves and Schack claim it's incorrect. Then---by the "eigenvalue-eigenstate link", which is a "minimalist" interpretation of the state vector's relation to actual observational outcomes, saying that if a state actually has a definite eigenvalue for some observable, than the outcome corresponding to that eigenvalue is actual (perhaps this can be thought of as assigning probabilities
if you like---just is an eigenstate of a "relative frequency operator" on this infinite tensor product Hilbert space, with eigenvalue equal to the Born probabilities. I believe that's the claim of the Farhi and Gutmann paper --- but Caves and Schack claim it's incorrect. Then---by the "eigenvalue-eigenstate link", which is a "minimalist" interpretation of the state vector's relation to actual observational outcomes, saying that if a state actually has a definite eigenvalue for some observable, than the outcome corresponding to that eigenvalue is actual (perhaps this can be thought of as assigning probabilities 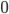 and
and  to outcome subspaces in which the state has zero component, or in which the state is contained, respectively)---one concludes that the Born rule probabilities are the only ones that give the correct relative frequencies, in the infinite limit.
to outcome subspaces in which the state has zero component, or in which the state is contained, respectively)---one concludes that the Born rule probabilities are the only ones that give the correct relative frequencies, in the infinite limit.
Whether or not the claim about the infinite state being an eigenstate of relative frequency is correct, I'm suspicious of arguments that require an actualized infinity---I try to understand them by understanding the actual limit as summarizing---albeit with some quantitative details of rates of convergence suppressed---how things "can be made to look in large finite cases"---i.e., the 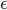 's and
's and 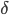 's rule my understanding. So---without having looked at the Farhi and Gutmann paper recently, however---let's think about this; it's something I've thought about before. Basically, it seems to me incorrect to claim that the state approaches an eigenstate of a sharp relative frequency operator---although the expectation value of its relative frequency list approaches the Born rule probabilities, as
's rule my understanding. So---without having looked at the Farhi and Gutmann paper recently, however---let's think about this; it's something I've thought about before. Basically, it seems to me incorrect to claim that the state approaches an eigenstate of a sharp relative frequency operator---although the expectation value of its relative frequency list approaches the Born rule probabilities, as 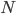 grows it remains in a superposition of eigenstates of the
grows it remains in a superposition of eigenstates of the 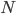 -th relative frequency operator. Indeed, as
-th relative frequency operator. Indeed, as 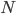 grows, if one projects out the relative frequencies nearest the Born ones containing a fixed large fraction---say 0.95---of the modulus squared of the state, there are more different frequency eigenvectors superposed as
grows, if one projects out the relative frequencies nearest the Born ones containing a fixed large fraction---say 0.95---of the modulus squared of the state, there are more different frequency eigenvectors superposed as 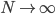 . Of course, the numerical range of the frequencies also converges around the Born rule ones, roughly as
. Of course, the numerical range of the frequencies also converges around the Born rule ones, roughly as 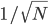 . It's a weak law of large numbers kind of thing---convergence in mean to the Born probabilities. But it's not convergence to an eigenstate of the frequency operator. This point, if I remember correctly, was first driven home to me by Ruediger Schack, at a time when I thought the convergence of most of the statevector modulus to a narrower and narrower range around the Born probabilities, was a pretty good argument that if you have to assign probabilities to outcomes in the Many Worlds interpretation, and you are willing to say that the probability assignment to a subspace should be uniformly continuous in the squared modulus of the state vector component in that subspace, then you should assign probabilities according to the Born rule.
. It's a weak law of large numbers kind of thing---convergence in mean to the Born probabilities. But it's not convergence to an eigenstate of the frequency operator. This point, if I remember correctly, was first driven home to me by Ruediger Schack, at a time when I thought the convergence of most of the statevector modulus to a narrower and narrower range around the Born probabilities, was a pretty good argument that if you have to assign probabilities to outcomes in the Many Worlds interpretation, and you are willing to say that the probability assignment to a subspace should be uniformly continuous in the squared modulus of the state vector component in that subspace, then you should assign probabilities according to the Born rule.
I no longer care so much about this argument. I now think the major issue for the Everett (Many Worlds) interpretation is whether one can reasonably use probabilistic notions at all, something that on my view this argument already presupposes one can do, as to neglect of a small-squared-modulus component of the wavefunction is effectively to declare that they have negligible probability, for the purposes at hand. At dinner, Alan argued that even classically, one has to neglect the large number of outcome sequences ---exponentially larger than the number of sequences having frequencies near the probabilities---to argue that frequencies will "typically" be near the probabilities, even classically. Neglecting a small-modulus portion of the state vector is thus no worse than what we do classically. From a Bayesian---or more particularly, subjectivist/decision-theoretic point of view on how probability enters into these matters---the point is that this is justified for many purposes by the low probability, of these sequences, whereas someone who truly believes that the value of probability as a guide to describing and deciding about the world comes from properties of frequencies, doesn't really have anything to say to justify this neglect. And there are things we can do to show that we cannot literally just treat all small probabilities as zero---for instance, we would not want to claim that, because the probability of each particular sequence of 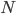 coin-toss outcomes is
coin-toss outcomes is 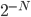 , we can ignore the possibility of getting a sequence with at least one tail, since each such sequence has negligible probability. But Alan wasn't buying a Bayesian point of view here---he said he was interested in predicting the frequencies with which things occur, not in betting. This is just a fundamental disagreement between us, and I tend to think that ultimately the frequentist point of view does not hang together sensibly, but this is not the point to go too far into it beyond what I said above about needing to presuppose probabilistic notions in order even to predict frequency.
, we can ignore the possibility of getting a sequence with at least one tail, since each such sequence has negligible probability. But Alan wasn't buying a Bayesian point of view here---he said he was interested in predicting the frequencies with which things occur, not in betting. This is just a fundamental disagreement between us, and I tend to think that ultimately the frequentist point of view does not hang together sensibly, but this is not the point to go too far into it beyond what I said above about needing to presuppose probabilistic notions in order even to predict frequency.
But let's return to a frame of mind in which one does care about such arguments, and see what the consequences area of adopting the continuity assumption I made above, i.e. roughly "vanishingly low modulus of amplitude implies vanishingly low probability". Does it really kill the argument to say that 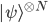 is not an eigenstate of any frequency operator? What about coarse-grained frequency operators, whose eigenspaces include subspaces spanned by the definite-frequency states with frequencies near the Born ones ? We can gloss the continuity assumption I described above by calling it the "almost-an-eigenstate rule": states with large enough amplitude in an eigenspace count as having the associated eigenvalue. This codifies Alan's "neglecting", and we may cash it out more delicately, for the subjectivist-inclined probabilist---in terms of a probabilistic assumption: that the probability of having an eigenstate is uniformly continuous in the modulus of the state's component in the associated eigenspace. This assumption is, at least, significantly weaker, at first glance, than assuming the Born rule straight away. And then it would seem to allow one to conclude, that the probability of observing relative frequencies close to the Born ones, grows with large
is not an eigenstate of any frequency operator? What about coarse-grained frequency operators, whose eigenspaces include subspaces spanned by the definite-frequency states with frequencies near the Born ones ? We can gloss the continuity assumption I described above by calling it the "almost-an-eigenstate rule": states with large enough amplitude in an eigenspace count as having the associated eigenvalue. This codifies Alan's "neglecting", and we may cash it out more delicately, for the subjectivist-inclined probabilist---in terms of a probabilistic assumption: that the probability of having an eigenstate is uniformly continuous in the modulus of the state's component in the associated eigenspace. This assumption is, at least, significantly weaker, at first glance, than assuming the Born rule straight away. And then it would seem to allow one to conclude, that the probability of observing relative frequencies close to the Born ones, grows with large 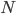 . More to the point, perhaps, the probability of observing any other relative frequencies, within the same tolerance, becomes negligible. At any
. More to the point, perhaps, the probability of observing any other relative frequencies, within the same tolerance, becomes negligible. At any 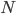 , of course, there will always be frequencies that we can't rule out. But it does look like only the Born rule is self-consistent in the sense that only for that rule will the amplitude of the states having frequencies within a shrinking interval of width proportional to
, of course, there will always be frequencies that we can't rule out. But it does look like only the Born rule is self-consistent in the sense that only for that rule will the amplitude of the states having frequencies within a shrinking interval of width proportional to 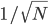 around the proposed probabilities, approach
around the proposed probabilities, approach  with increasing
with increasing 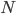 .
.
I should probably think a bit more about things before posting this since there may be some elementary objection to the considerations I've just given, but as it's a blog, what the heck---I'll leave this hanging in the void of cyberspace for now, and risk being shown up by some comment, though this would appear unlikely if the past is any guide...
One parting point is that there are more comments on this issue in Matt Leifer's blog, under the neutral title "Anyone for Frequentist Fudge?", which I came across while working on this post, and recomend highly. Matt objects to assiging "worlds with small amplitudes a small probability (which we do not do because that is what we're trying to derive". I tend to agree, but strictly speaking it's only part of what we're trying to derive, so it's at least interesting that---if you buy the apparatus of 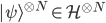 for representing independent trials, which I guess is pretty standard (although Peter Byrne (see previous post) seemed to be claiming Everett may have introduced it)---you appear to be able to get from it, to a demonstration that only the Born probabilities satisfy the self-consistency property I described above.
for representing independent trials, which I guess is pretty standard (although Peter Byrne (see previous post) seemed to be claiming Everett may have introduced it)---you appear to be able to get from it, to a demonstration that only the Born probabilities satisfy the self-consistency property I described above.
Foundational Questions in the Azores I: Peter Byrne on Hugh Everett and Many Worlds
So far, there hasn't been much physics in Wine, Physics, and Song---nor much song, for that matter, though there's been plenty of wine, and some economics and politics. I guess wine is easier and more relaxing to write about. But it's time to redress that balance.
I arrived in Ponta Delgada, the main town of the island of São Miguel in the Portuguese archipelago of the Azores, courtesy of the Foundational Questions Institute, to attend and speak at their second annual conference. We were treated to dinner and an after-dinner talk. (The wines, especially a white called something like Tierra de Lavas that was served before dinner, were tasty.) The talk was by Peter Byrne, who is writing a biography of Hugh Everett III, the originator (unless you want to ascribe it to Schrödinger in his cat paper) of what he called the "relative state" interpretation of quantum mechanics, often called the "many worlds interpretation" (MWI). I was particularly interested in this talk because a fascination with the problem of how to interpret quantum theory is a large part of what got me into physics. In 1989--1990 I wrote a paper (unpublished), "The Many-Worlds Interpretation of Quantum Mechanics: Psychological versus Physical Bases for the Multiplicity of "Worlds", arguing that Everett's interpretation had often been misunderstood as involving a "physical" splitting of the universe into different branches, whereas Everett was actually fairly clear that the "branching" into parts of the universe involving different outcomes of a quantum experiment was associated with different subspaces of a single Hilbert space of the world, subspaces defined by which of the different macroscopic outcomes of the experiment an observer had experienced. So I was very interested to hear from Peter Byrne that among the boxes of Everett's paper that he has been sorting and studying, were drafts of Everett's thesis in which there is much more extensive discussion of splitting minds than was available even in the long version of his thesis published by Princeton. If I'm reporting Byrne correctly, one of these drafts compares the splitting minds to splitting amoebas, noting there is no fact of the matter as to which of the amoebas is the original one. The whole thing, he says, had much more extensive discussion of splitting, which his advisor John Wheeler made him take out (partly, if I understood correctly, because of negative comments by Bohr, relayed by Stern who was on Everett's thesis committee). It will be interesting to see the details of these drafts, and find out more about how Everett understood this "splitting".
My early paper was to some extent a "devil's advocate" exercise---I did not then, and do not now, believe in Everett's interpretation in the sense that a macroscopically entangled wavefunction, describing me having all kinds of different conscious experiences, is a real entity. But I did believe, and still do, that pushing Everett's idea as far as possible is one good way of getting a better understanding of what is weird about quantum theory, and of the unexpected difficulties we've encountered in figuring out what quantum physics has to tell us about the world, and our place in it.
My reasons for not accepting many worlds are in part tied up with the fact that there don't seem to be probabilities of measurement outcomes on this interpretation, as there are indeed not definite classical outcomes. More on this later---it is something that I've been thinking about for years, and before Byrne's talk, I had a long discussion about it with Alan Guth at dinner. But one last thing: it was therefore striking to hear from Byrne that one of a myriad of titles Everett considered for his dissertation was "Wave mechanics without probability".
National Strategy Workshop on Quantum Information Science
Next week, I'll be at a workshop in Vienna, VA that has been organized to help come up with a national strategy for public investment in quantum information science and technology.
To quote from the workshop website:
This Workshop on Quantum Information Science (QIS) has been organized in response to the NSTC report. It brings together leading theorists and experimenters drawn from physical science, computer science, mathematics, and engineering who will assess recent progress in QIS and identify major goals and challenges for future research.
The report in question, titled "A Federal Vision for Quantum Information Science came out this January, from the US National Science and Technology Council which is part of the White House's Office of Science and Technology Policy.
All in all, a very interesting and promising development, which suggests serious potential for US government support for research in quantum information science, which is to say quantum computation, quantum computing, quantum cryptography, the use of quantum information science concepts to understand and engineer the behavior of complex physical systems, including quantum control and quantum metrology. The report emphasizes computation and the understanding of new quantum states of matter and quantum phase transitions. The organization appears to have been fairly rapid---probably carried out at Caltech, where John Preskill heads the Institute for Quantum Information, since that's where the website is located and the administrative coordinator is the IQI's.
The invited speaker lineup looks excellent, though some have complained that it's not representative of some aspects of quantum information research (metrology, i.e. precision quantum measurement, is covered only lightly) and some top US groups (like the quantum cryptography effort led by Richard Hughes at Los Alamos) are missing (though I don't know why). Evenings will involve open discussions on strategy for QIS research, though I worry we may be burned out after full days of excellent technical presentations.
I'm looking forward to hearing Anne Broadbent talk about Universal Blind Quantum Computation with Joseph Fitzsimmons and Elham Kashefi, and not only because a crucial component of it is the use of quantum authentication codes, a concept developed my collaborators Claude Crepeau, Daniel Gottesman, Adam Smith, Alain Tapp, and me. (Hey, this is my blog, so shameless self-promotion is de rigeur.)


