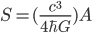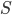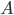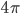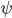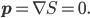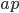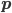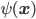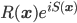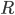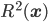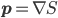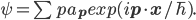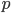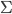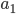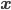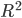I'm in Cambridge, where the conference on Free Will and Retrocausality in the Quantum World, organized (or rather, organised) by Huw Price and Matt Farr will begin in a few hours. (My room at St. Catherine's is across from the chapel, and I'm being serenaded by a choir singing beautifully at a professional level of perfection and musicality---I saw them leaving the chapel yesterday and they looked, amazingly, to be mostly junior high school age.) I'm hoping to understand more about how "retrocausality", in which effects occur before their causes, might help resolve some apparent problems with quantum theory, perhaps in ways that point to potentially deeper underlying theories such as a "quantum gravity". So, as much for my own use as anyone else's, I thought perhaps I should post about my current understanding of this possibility.
One of the main problems or puzzles with quantum theory that Huw and others (such as Matthew Leifer, who will be speaking) think retrocausality may be able to help with, is the existence of Bell-type inequality violations. At their simplest, these involve two spacelike-separated regions of spacetime, usually referred to as "Alice's laboratory" and "Bob's laboratory", at each of which different possible experiments can be done. The results of these experiments can be correlated, for example if they are done on a pair of particles, one of which has reached Alice's lab and the other Bob's, that have previously interacted, or were perhaps created simultaneously in the same event. Typically in actual experiments, these are a pair of photons created in a "downconversion" event in a nonlinear crystal. In a "nonlinear" optical process photon number is not conserved (so one can get a "nonlinearity" at the level of a Maxwell's equation where the intensity of the field is proportional to photon number; "nonlinearity" refers to the fact that the sum of two solutions is not required to be a solution). In parametric downconversion, a photon is absorbed by the crystal which emits a pair of photons in its place, whose energy-momentum four-vectors add up to that of the absorbed photon (the process does conserve energy-momentum). Conservation of angular momentum imposes correlations between the results of measurements made by "Alice" and "Bob" on the emitted photons. These are correlated even if the measurements are made sometime after the photons have separated far enough that the changes in the measurement apparatus that determine which component of polarization it measures (which we'll henceforth call the "polarization setting"), on one of the photons, are space-like separated from the measurement process on the other photon, so that effects of the polarization setting in Alice's laboratory, which one typically assumes can propagate only forward in time, i.e. in their forward light-cone, can't affect the setting or results in Bob's laboratory which is outside of this forward light-cone. (And vice versa, interchanging Alice and Bob.)
Knowledge of how their pair of photons were prepared (via parametric downconversion and propagation to Alice and Bob's measurement sites) is encoded in a "quantum state" of the polarizations of the photon pair. It gives us, for any pair of polarization settings that could be chosen by Alice and Bob, an ordinary classical joint probability distribution over the pair of random variables that are the outcomes of the given measurements. We have different classical joint distributions, referring to different pairs of random variables, when different pairs of polarization settings are chosen. The Bell "paradox" is that there is no way of introducing further random variables that are independent of these polarization settings, such that for each pair of polarization settings, and each assignment of values to the further random variables, Alice and Bob's measurement outcomes are independent of each other, but when the further random variables are averaged over, the experimentally observed correlations, for each pair of settings, are reproduced. In other words, the outcomes of the polarization measurements, and in particular the fact that they are correlated, can't be "explained" by variables uncorrelated with the settings. The nonexistence of such an explanation is implied by the violation of a type of inequality called a "Bell inequality". (It's equivalent to to such a violation, if "Bell inequality" is defined generally enough.)
How I stopped worrying and learned to love quantum correlations
One might have hoped to explain the correlations by having some physical quantities (sometimes referred to as "hidden variables") in the intersection of Alice and Bob's backward light-cone, whose effects, propagating forward in their light-cone to Alice and Bob's laboratories, interact their with the physical quantities describing the polarization settings to produce---whether deterministically or stochastically---the measurement outcomes at each sites, with their observed probabilities and correlations. The above "paradox" implies that this kind of "explanation" is not possible.
Some people, such as Tim Maudlin, seem to think that this implies that quantum theory is "nonlocal" in the sense of exhibiting some faster-than-light influence. I think this is wrong. If one wants to "explain" correlations by finding---or hypothesizing, as "hidden variables"---quantities conditional on which the probabilities of outcomes, for all possible measurement settings, factorize, then these cannot be independent of measurement settings. If one further requires that all such quantities must be localized in spacetime, and that their influence propagates (in some sense that I'm not too clear about at the moment, but that can probably be described in terms of differential equations---something like a conserved probability current might be involved) locally and forward in time, perhaps one gets into inconsistencies. But one can also just say that these correlations are a fact. We can have explanations of these sorts of fact---for example, for correlations in photon polarization measurements, the one alluded to above in terms of energy-momentum conservation and previous interaction or simultaneous creation---just not the sort of ultra-classical one some people wish for.
Retrocausality
It seems to me that what the retrocausality advocates bring to this issue is the possibility of something that is close to this type of classical explanation. It may allow for the removal of these types of correlation by conditioning on physical quantities. [Added July 31: this does not conflict with Bell's theorem, for the physical quantities are not required to be uncorrelated with measurement settings---indeed, being correlated with the measurement settings is to be expected if there is retrocausal influence from a measurement setting to physical quantities in the backwards light-cone of the measurement setting.] And unlike the Bohmian hidden variable theories, it hopes to avoid superluminal propagation of the influence of measurement settings to physical quantities, even unobservable ones. It does this, however, by having the influence of measurement settings pursue a "zig-zag" path from Alice to Bob: in Alice's backward light-cone back to the region where Alice and Bob's backward light-cones intersect, then forward to Bob's laboratory. What advantages might this have over superluminal propagation? It probably satisfies some kind of spacetime continuity postulate, and seems more likely to be able to be Lorentz-invariant. (However, the relation between formal Lorentz invariance and lack of superluminal propagation is subtle, as Rafael Sorkin reminded me at breakfast today.)