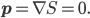Tag Archives: quantum mechanics

Bohm on measurement in Bohmian quantum theory

Posted on by

Prompted, as described in the previous post, by Craig Callender's post on the uncertainty principle, I've gone back to David Bohm's original series of two papers "A suggested interpretation of the quantum theory in terms of "hidden" variables I" and "...II", published in Physical Review in 1952 (and reprinted in Wheeler and Zurek's classic collection "Quantum Theory and Measurement", Princeton University Press, 1983).  The Bohm papers and others appear to be downloadable here.

Question 1 of my previous post asked whether it is true that

"a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus."

It is fairly clear from Bohm's papers that the answer is "Yes". In section 5 of the second paper, he writes

"in the measurement of an "observable," Q, we cannot obtain enough information to provide a complete specification of the state of an electron, because we cannot infer the precisely defined values of the particle momentum and position, which are, for example, needed if we wish to make precise predictions about the future behavior of the electron. [...] the measurement of an "observable" is not really a measurement of any physical property belonging to the observed system alone. Instead, the value of an "observable" measures only an incompletely predictable and controllable potentiality belonging just as much to the measuring apparatus as to the observed system itself."

Since the first sentence quoted says we cannot infer precise values of "momentum and position", it is possible to interpret it as referring to an uncertainty-principle-like tradeoff of precision in measurement of one versus the other, rather than a statement that it is not possible to measure either precisely, but I think that would be a misreading, as the rest of the quote, which clearly concerns any single observable, indicates. Later in the section, he unambiguously gives the answer "Yes" to a mutation of my Question 1 which substitutes momentum for position. Indeed, most of the section is concerned with using momentum measurement as an example of the general principle that the measurements described by standard quantum theory, when interpreted in his formalism, do not measure pre-existing properties of the measured system.

Here's a bit of one of two explicit examples he gives of momentum measurement:

"...consider a stationary state of an atom, of zero angular momentum. [...] the -field for such a state is real, so that we obtain

Thus, the particle is at rest. Nevertheless, we see from (14) and (15) that if the momentum "observable" is measured, a large value of this "observable" may be obtained if the -field happens to have a large fourier coefficient, , for a high value of . The reason is that in the process of interaction with the measuring apparatus, the -field is altered in such a way that it can give the electron particle a correspondingly large momentum, thus transferring some of the potential energy of interaction of the particle with its -field into kinetic energy."

Note that the Bohmian theory involves writing the complex-valued wavefunction 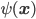as 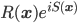, i.e. in terms of its (real) modulus 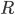and (real) phase 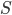. Expressing the Schrödinger equation in terms of these variables is in fact probably what suggested the interpretation, since one gets something resembling classical equations of motion, but with a term that looks like a potential, but depends on 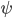. Then one takes these classical-like equations of motion seriously, as governing the motions of actual particles that have definite positions and momenta. In order to stay in agreement with quantum theory concerning observed events such as the outcomes of measurements, m theory, one in addition keeps, from quantum theory, the assumption that the wavefunction 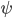evolves according to the Schrödinger equation. And one assumes that we don't know the particles' exact position but only that this is distributed with probability measure given (as quantum theory would predict for the outcome of a position measurement) by 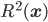, and that the momentum is 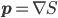. That's why the real-valuedness of the wavefunction implies that momentum is zero: because the momentum, in Bohmian theory, is the gradient of the phase of the wavefunction.

For completeness we should reproduce Bohm's (15).

(15)

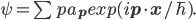
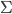At least in the Wheeler and Zurek book, the equation has instead of as the subscript on , and 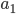instead of 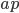; I consider these typos, and have corrected them. (Bohm's reference to (14), which is essentially the same as (15) seems to me to be redundant.)

The upshot is that

"the actual particle momentum existing before the measurement took place is quite different from the numerical value obtained for the momentum "observable,"which, in the usual interpretation, is called the "momentum." "

It would be nice to have this worked out for a position measurement example, as well. The nicest thing, from my point of view, would be an example trajectory, for a definite initial position, under a position-measurement interaction, leading to a final position different from the initial one. I doubt this would be too hard, although it is generally considered to be the case that solving the Bohmian equations of motion is difficult in the technical sense of complexity theory. I don't recall just how difficult, but more difficult than solving the Schrödinger equation, which is sometimes taken as an argument against the Bohmian interpretation: why should nature do all that work, only to reproduce, because of the constraints mentioned above---distribution of 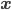according to 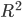, 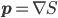---observable consequences that can be more easily calculated using the Schrödinger equation?
I think I first heard of this complexity objection (which is of course something of a matter of taste in scientific theories, rather than a knockdown argument) from Daniel Gottesman, in a conversation at one of the Feynman Fests at the University of Maryland, although Antony Valentini (himself a Bohmian) has definitely stressed the ability of Bohmian mechanics to solve problems of high complexity, if one is allowed to violate the constraints that make it observationally indistinguishable from quantum theory. It is clear from rereading Bohm's 1952 papers that Bohm was excited about the physical possibility of going beyond these constraints, and thus beyond the limitations of standard quantum theory, if his theory was correct.

In fairness to Bohmianism, I should mention that in these papers Bohm suggests that the constraints that give standard quantum behavior may be an equilibrium, and in another paper he gives arguments in favor of this claim. Others have since taken up this line of argument and done more with it. I'm not familiar with the details. But the analogy with thermodynamics and statistical mechanics breaks down in at least one respect, that one can observe nonequilibrium phenomena, and processes of equilibration, with respect to standard thermodynamics, but nothing like this has so far been observed with respect to Bohmian quantum theory. (Of course that does not mean we shouldn't think harder, guided by Bohmian theory, about where such violations might be observed... I believe Valentini has suggested some possibilities in early-universe physics.)

Nagel and DeLong I: Common Sense

Posted on by

Brad DeLong has been hammering --- perhaps even bashing --- away at Thomas Nagel's new book Mind and Cosmos (Oxford, 2012).  Here's a link to his latest blow. I think Nagel's wrong on several key points in that book, but I think Brad is giving people a misleading picture of Nagel's arguments.  This matters because Nagel has made very important points --- some of which are repeated in this book, though more thoroughly covered in his earlier The Last Word (Oxford, 1997) --- about the nature of reason, defending the possibility of achieving, in part through the use of reason, objectively correct knowledge (if that is the right word) in areas other than science, and giving us some valuable ideas about how this can work in particular cases, for example, in the case of ethics, in The Possibility of Altruism [Princeton, 1979].

In his latest salvo Brad suggests that "If you are going to reject any branch of science on the grounds that it flies in the face of common sense, require[s] us to subordinate the incredulity of common sense, is not based ultimately on common sense, or is a heroic triumph of ideological theory over common sense--quantum mechanics is definitely the place to start…".  This is preceded by some quotes from Nagel:

  • But it seems to me that, as it is usually presented, the current orthodoxy about the cosmic order is the product of governing assumptions that are unsupported, and that it flies in the face of common sense…
  • My skepticism is… just a belief that the available scientific evidence, in spite of the consensus of scientific opinion, does not… rationally require us to subordinate the incredulity of common sense…
  • Everything we believe, even the most far-reaching cosmological theories, has to be based ultimately on common sense, and on what is plainly undeniable…
  • I have argued patiently against the prevailing form of naturalism, a reductive materialism that purports to capture life and mind through its neo-Darwinian extension…. I find this view antecedently unbelievable— a heroic triumph of ideological theory over common sense…

Now there are things I disagree with here, but Nagel is clearly not claiming that no theory that is not itself a piece of common sense is acceptable. Indeed, the second bullet point makes it clear that he allows for the possibility that scientific evidence could "rationally require" him to subordinate the incredulity of common sense. It is his judgment that it does not in this case. Now---at least with regard to the possibility of an explanation by evolutionary biology of the emergence of life, consciousness, and reason on our planet and in our species, which is what I think is at issue--- I don't share his incredulity, and I also suspect that I would weigh the scientific evidence much more heavily against such incredulity, if I did share some of it.  But Nagel is not commited to a blanket policy of "reject[ing] scientific theories because they fail to match up to your common sense." Regarding the third bullet point, it's perhaps stated in too-strong terms, but it's far from a claim that every scientific theory can directly be compared to common sense and judged on that basis. The claim that scientific theories are "ultimately based in common sense and on what is plainly undeniable" does not imply that this basis must be plain and direct. Logic and mathematics develop out of common-sense roots, counting and speaking and such... science develops to explain "plainly undeniable" results of experiments, accounts of which are given in terms of macroscopic objects... Some of this smacks a bit too much of notions that may have proved problematic for positivism ("plainly undeniable" observation reports?)... but the point is that common sense carries some weight and indeed is a crucial element of our scientific activities, not that whatever aspect of "common sense" finds quantum theory hard to deal with must outweigh the enormous weight of scientific experience and engineering practice, also rooted "ultimately" according to Nagel in common sense, in favor of that theory.

Just for the record I don't find that the bare instrumentalist version of quantum theory as an account of the probabilities of experimental results "flies in the face of common sense" --- but it does seem that it might create serious difficulty for the conception of physical reality existing independent of our interactions with it. At any rate it does not seem to provide us with a picture of that sort of physical reality (unless you accept the Bohm or Everett interpretations), despite what one might have hoped for from a formalism that is used to describe the behavior of what we tend to think of as the basic constituents of physical reality, the various elementary particles or better, quantum fields.  But if someone, say Nagel, did believe that this all flies in the face of common sense, it would be open to him to say that in this case, we are permitted, encourage, or perhaps even required to fly in said face by the weight of scientific evidence.

As I've said, I disagree on two counts with Nagel's skepticism about an evolutionary explanation of mind and reason: it doesn't fly in the face of my common sense, and I weigh the evidence as favoring it more strongly than does Nagel. Part of my disagreement may be that what Nagel has in mind is an evolutionary explanation that is commited to a "reductive materialism that purports to capture life and mind through its neo-Darwinian extension." Whereas I have in mind a less reductive approach, in which consciousness and reason are evolutionarily favored because they have survival value, but we do not necessarily reduce these concepts themselves to physical terms. In my view, biology is rife with concepts that are not physical, nor likely to be usefully reduced to physical terms--- like, say, "eye". As with "eye", there may be no useful reduction of "consciousness" or "perception" or "thought" or "word" or "proposition", etc.., to physics, but I don't think that implies that the appearance of such things cannot have an evolutionary explanation. (Nor, just to be clear, does it imply that these things are not realized in physical processes.) So I might share Nagel's incredulity that such things could have a "materialist" explanation, if by this he means one in terms of physics, but not his incredulity about evolutionary explanations of the appearance of mind and reason. To me, it seems quite credible that these phenomena form part of the mental aspect of structures made of physical stuff, though we will never have full explanations for all the phenomena of consciousness and the doings of reason, in terms of this physical structure.

(David Deutsch's recent book The Beginning of Infinity is one excellent source for understanding such non-reductionism---see in particular its Chapter 5, "The Reality of Abstractions".)

I'll likely make several more posts on this business, both on other ways in which I think Brad and others have mischaracterized Nagel's arguments or misplaced the emphasis in their criticisms, and on why this matters because some important points that Nagel has made on matters closely related to these, that I think have value, are in danger of being obscured, caricatured, or dismissed under the influence of the present discussion by Brad and others.