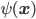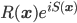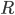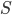The Marriage of Figaro, Santa Fe 2013

Posted on by

The 2013 opera season at Santa Fe ended last night (well, two nights ago as this is posted) with a performance of Offenbach's comic operetta The Grand Duchess of Gerolstein.  I went to all five operas, and thought this one of the strongest seasons I've been to at Santa Fe.  As the first installment of a report on the season, I'll cover the August 20th performance of Mozart's The Marriage of Figaro.

This was the first time I've seen this opera, though I have a video of it I used to enjoy.  Figaro is well known to be one of the greatest and most enjoyable operas so I won't cover the basics; if you think you might be interested in opera, it is one of the first ones you should get to know, particularly if you are looking for something combining melodic beauty, at times soaring, at times restrained, with elegance and lightness of spirit. (If you're looking for more consistently over-the-top emotion and big tunes, like perhaps if you're into metal or arena rock and looking to explore opera, the "big three" operas of Verdi's middle period (La Traviata, Rigoletto, Il Trovatore), or even more over-the-top, the big Puccinis (especially Tosca or Madama Butterfly, also Turandot) are probably the ticket for an introduction to opera.)   All elements of this production were top-notch.  In Phillips, Fons, Oropesa, and Nelson, and probably several others, it featured some of the best singers I've heard at Santa Fe.  Susanna Phillips as the Countess and Emily Fons as Susanna were in beautiful form, both with strong, sweet voices, Phillips a soprano, Fons a very lyric mezzo.  The opera moves from the first act's exposition, silly business and plotting into more serious emotional territory with the Countess' first appearance, in the opening scene of Act II, in the beautiful lament Porgi, amor, qualche ristoro (Give me, love, some solace). Phillips portrayed the Countess' emotion superbly, with great dynamic control and plenty of power and projection when necessary without forcing the voice or losing sweetness of tone. Another in our party disliked the somewhat broad vibrato she unleashed at times, but I thought it was just right, part of a classic powerful operatic soprano presentation that still remained controlled and appropriate for Mozart. She was also superb in ensembles, and in her other major aria, the third act's Dove sono i bei momenti (Where are those beautiful moments?), especially the allegro section (Ah! se almen la mia costanza... (Oh! If only my constancy...)) that ends it. (I'm not sure if the notion of a fast cabaletta to cap off a broad aria had developed by this time, or if Mozart was helping to invent it here.) If I have any minor complaint about Phillips' singing, it might be that although her pianissimo singing can be incredibly sweet, it occasionally was so soft, the dynamic contrast so great, that it seemed a bit mannered, especially when used to end a phrase on a high note (more difficult, to be sure, than a loud high note, and achieved here with perfect control). But this is a very minor cavil and could be completely baseless, not even apparent from a different seat with different acoustics. (The member of our party who objected to Phillips' vibrato singled out her piano singing for special praise.) Overall, I thought this was opera singing of the highest caliber, in which the musicality of Phillips' phrasing and the beauty of her voice were inseparable from the communication of emotion and through it, her part in the the development of the drama.

The Santa Fe New Mexican, in a glowing review of the June 29th performance, wrote that

Phillips took a while to settle in, as Countesses often do, but she arrived at a firm, full-throated performance. Her voice has been evolving impressively in recent years, and one senses that she may be on the verge of the vocal luxuriance that has marked the most memorable Countesses over the years.

Her relationship with the role must have continued evolving in the month and a half since that early performance, because vocal luxuriance was abundantly, though not overbearingly, present, she needed no time to settle in, but had me by the heartstrings from the first notes of "Porgi, amor", and her performance will certainly live in my memory.

In the "trouser role" of Cherubino, soprano Emily Fons was equally superb. She did a good job with the comic elements of the character (a young boy discovering the delights of love with various local girls, and infatuated with the Countess as well---"Narciseto, Adoncino de amor", as Figaro characterizes him in the famous aria "Non piu andrai, farfallone amoroso, notte e giorno d'intorno girando, delle belle turbando il riposo" (No longer will you go, amorous butterfly, running around night and day disturbing the peace of pretty girls" ) with which he bids him goodbye as the Count attempts (unsuccessfully, it turns out) to send him away to join the army). The comedy was perhaps a bit muggy and telegraphed, the makeup a bit heavy viewed with binoculars, but that's probably part of such a role, and Fons kept it light and flitty, like an amorous butterfly indeed. Her voice is as good as Phillips', just slightly smoother and lighter in tone, and with a bit less prominent vibrato, but still quite full and sweet, definitely a sweetly lyric rather than a throaty mezzo, hence perfect, in my judgement, for this role. Her Voi che sapete, che cosa e l'amore ("You who know what love is"), yet another of the many classic arias you probably know even if you've never attended the opera or listened to it on your stereo (or phone, pad, pod, or computer), was as good as I can imagine. I will count either of these artists, Fons or Phillips, as among the best women singing today and reason enough to attend any opera they're in; keep a lookout for them if you follow opera. As Susanna, Lisette Oropesa's performance was of similar caliber; I don't remember specific moments as moving as the abovementioned arias of the Contessa and of Cherubino, but find myself wishing I could attend another performance to focus more on Susanna; her acting and singing were, as far as I can recall, flawless and her voice, like the other women's, clear, unstrained and musical, and carried well in what may be a slightly difficult (because open at the sides) theater.

Zachary Nelson did a superb job as Figaro. He is clearly---and with reason---rising very fast in the world of opera, as he was in the apprentice singer program last summer (2012) at Santa Fe. His performance was completely assured, his acting and musicality top-notch, with nothing to indicate anything but a seasoned and confident singer. Strangely, before looking in the program and finding out how recently he'd been an apprentice, I got the impression, just from his very pleasing tone, of a relatively young voice, perhaps in transition to a fuller, darker voice. That's arguably quite appropriate for Figaro, who is already quite competent and arguably making a similar transition from youthful adulthood to maturity, with marriage in view. He had plenty of power, never oversung or forced and achieved good projection, with perhaps occasional slight loss of power on the very lowest notes, or just slightly falling in the shadow of one of the sopranos (always a bit difficult for a baritone to balance with a powerful soprano, I suspect). But again, I could be off-base with such minor cavils, and overall this was a consistently excellent performance, probably the best by a baritone that I heard this season at Santa Fe, with excellent musicality and control in both solo and ensemble situations, a very interesting voice with some color and texture to it (making me think of walnut with a natural oil finish, maybe very fine tweed) but also a kind of clarion, though not cutting or harsh, quality that helps it stand out and project.  Wonderful, balanced characterization of Figaro, carried through ensemble, recitative and conversational duets and also solo arias,  lighthearted and witty, yet competent and with seriousness of purpose.  Se vuol ballare, signor contino ("If you want to dance, little Mr. Count") was a perfect example, with an overall affect of restrained glee at the prospect of teaching the Count a lesson, but not completely without menace and genuine outrage, either.  Non piu andrai was similarly deftly done.  Nelson is definitely another singer to go out of your way to hear.

Daniel Okulitch's Count was also extremely well sung and acted.  Though it still has some depth, his voice is perhaps is a little harder-edged and more brilliant than Nelson's, which seemed to suit his more authoritarian and rigid character.  The part doesn't offer as many star turns as does Figaro, but Okulitch played it perfectly.

I would have had to attend multiple times (I know a guy who goes to multiple performances of each opera, getting standing room to make it affordable) in order to evaluate the supporting singers with any accuracy; such evaluation is not really what I want to focus when I'm going once to enjoy an opera. What I can say is that overall the supporting singers were very solid, with no weaknesses that I noticed.  Keith Jameson, as the music master Basilio, stood out not only because he was a tenor (the heroic or lead-lover tenor was perhaps less established in Mozart's day, especially, I guess, in comic opera), but for the excellence and clarity of his voice and pacing, and Rachel Hall as Barbarina had a noticeably pleasing voice and sang well also.  A really excellent ensemble cast and chorus.

The production was excellent too, true to the original setting of the play and beautifully detailed, doing a wonderful job of creating a believable setting in an eighteenth-century aristocratic estate without needing to go over the top, fitting seamlessly with the particular requirements of Santa Fe's stage. The (presumably artificial) bunches of flowers planted all over the stage, and removed by topcoated and bewigged aristocrats from the front portion of the stage during the latter part of the overture, leaving the ones in back to serve as the garden exterior to the house when appropriate, were a spectacular and creative touch. Costumes were period-appropriate, with luxurious detail where appropriate but still lively and fresh rather than stodgy.

I didn't focus too hard on the orchestra's performance, conducted by John Nelson, but can say that it was light, lively, elegant, and integrated well with the vocal work. Obviously, no flaws drew unwanted attention to it. An instance of particularly memorable and perfectly-executed orchestral playing was the eighteen bars before the Count's famous plea for forgiveness "Contessa, perdono" , accompanying the Count's realization of the last of many deceptions that have been played on him ("O cielo, che veggio...", Oh heavens, what do I see...", sung by the Count, Dr. Bartolo the music teacher, Basilio, and Antonio the gardener.  (This passage begins with the second system on page 343 in the BMG/Ricordi piano/vocal score, or on page 48 of the pdf (390 of the original) of the full score from Peters, other sections downloadable here.)  The orchestra takes off in with running eight notes, scalar passages with frequent direction changes and turn-like flourishes, rapidly modulating through major and minor keys, including some fairly remote ones like Eb major (the ambient key signature is G major although the section starts in G minor), with a cascade down the cycle of fifths from G to Bb in the middle of the section, for a somewhat unearthly, magical, flying feeling creating an atmosphere like that in parts of the Magic Flute.  There is some baroque influence evident especially when the line does something ornamental, but it is not pastiche, definitely something new and probably uniquely Mozartean.  The passage is also reminiscent of a recurrent motif in Mozart's next opera on a Da Ponte libretto, Don Giovanni, which however features somewhat more regular ascending and then descending scales in minor, the whole ascending descending figure repeating in higher and higher keys, for a similar effect of suddenly becoming unmoored from ordinary reality and gliding through an eerily magical realm, but in a more tension-building, and definitely ominous, way. These eighteen bars are one of the many pinnacles of Mozartean magic reached in this opera. I recently read (it would have been in a collection "Other Entertainment" of Ned Rorem's essays, or in Dietrich Fischer-Dieskau's memoirs or Gerald Moore's book The Schubert Song Cycles) an approvingly quoted aphorism along the lines of "The only thing that matters in music is that which cannot be explained", and it is tempting to think of this passage as an example of such inexplicable magic, except that I think that while it's absolutely magical, it's mostly quite explicable---some of the discussion above is a start, and the passage would clearly repay more careful analysis, which I may do and post separately. Such analysis is probably more important to one who wants to understand how to achieve similar effects, rather than one who just wants to enjoy the magic... Mozart and a good opera orchestra like Santa Fe's are enough to ensure the latter. With a superb vocal cast and excellence in all aspects of production, this added up to a production that --- although I've not seen another live Figaro --- would be hard to top, an evening filled with all manner of Mozartean magic.

Bohm on measurement in Bohmian quantum theory

Posted on by

Prompted, as described in the previous post, by Craig Callender's post on the uncertainty principle, I've gone back to David Bohm's original series of two papers "A suggested interpretation of the quantum theory in terms of "hidden" variables I" and "...II", published in Physical Review in 1952 (and reprinted in Wheeler and Zurek's classic collection "Quantum Theory and Measurement", Princeton University Press, 1983).  The Bohm papers and others appear to be downloadable here.

Question 1 of my previous post asked whether it is true that

"a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus."

It is fairly clear from Bohm's papers that the answer is "Yes". In section 5 of the second paper, he writes

"in the measurement of an "observable," Q, we cannot obtain enough information to provide a complete specification of the state of an electron, because we cannot infer the precisely defined values of the particle momentum and position, which are, for example, needed if we wish to make precise predictions about the future behavior of the electron. [...] the measurement of an "observable" is not really a measurement of any physical property belonging to the observed system alone. Instead, the value of an "observable" measures only an incompletely predictable and controllable potentiality belonging just as much to the measuring apparatus as to the observed system itself."

Since the first sentence quoted says we cannot infer precise values of "momentum and position", it is possible to interpret it as referring to an uncertainty-principle-like tradeoff of precision in measurement of one versus the other, rather than a statement that it is not possible to measure either precisely, but I think that would be a misreading, as the rest of the quote, which clearly concerns any single observable, indicates. Later in the section, he unambiguously gives the answer "Yes" to a mutation of my Question 1 which substitutes momentum for position. Indeed, most of the section is concerned with using momentum measurement as an example of the general principle that the measurements described by standard quantum theory, when interpreted in his formalism, do not measure pre-existing properties of the measured system.

Here's a bit of one of two explicit examples he gives of momentum measurement:

"...consider a stationary state of an atom, of zero angular momentum. [...] the -field for such a state is real, so that we obtain

Thus, the particle is at rest. Nevertheless, we see from (14) and (15) that if the momentum "observable" is measured, a large value of this "observable" may be obtained if the -field happens to have a large fourier coefficient, , for a high value of . The reason is that in the process of interaction with the measuring apparatus, the -field is altered in such a way that it can give the electron particle a correspondingly large momentum, thus transferring some of the potential energy of interaction of the particle with its -field into kinetic energy."

Note that the Bohmian theory involves writing the complex-valued wavefunction as , i.e. in terms of its (real) modulus and (real) phase . Expressing the Schrödinger equation in terms of these variables is in fact probably what suggested the interpretation, since one gets something resembling classical equations of motion, but with a term that looks like a potential, but depends on . Then one takes these classical-like equations of motion seriously, as governing the motions of actual particles that have definite positions and momenta. In order to stay in agreement with quantum theory concerning observed events such as the outcomes of measurements, m theory, one in addition keeps, from quantum theory, the assumption that the wavefunction evolves according to the Schrödinger equation. And one assumes that we don't know the particles' exact position but only that this is distributed with probability measure given (as quantum theory would predict for the outcome of a position measurement) by , and that the momentum is . That's why the real-valuedness of the wavefunction implies that momentum is zero: because the momentum, in Bohmian theory, is the gradient of the phase of the wavefunction.

For completeness we should reproduce Bohm's (15).

(15)

At least in the Wheeler and Zurek book, the equation has instead of as the subscript on , and instead of ; I consider these typos, and have corrected them. (Bohm's reference to (14), which is essentially the same as (15) seems to me to be redundant.)

The upshot is that

"the actual particle momentum existing before the measurement took place is quite different from the numerical value obtained for the momentum "observable,"which, in the usual interpretation, is called the "momentum." "

It would be nice to have this worked out for a position measurement example, as well. The nicest thing, from my point of view, would be an example trajectory, for a definite initial position, under a position-measurement interaction, leading to a final position different from the initial one. I doubt this would be too hard, although it is generally considered to be the case that solving the Bohmian equations of motion is difficult in the technical sense of complexity theory. I don't recall just how difficult, but more difficult than solving the Schrödinger equation, which is sometimes taken as an argument against the Bohmian interpretation: why should nature do all that work, only to reproduce, because of the constraints mentioned above---distribution of according to , ---observable consequences that can be more easily calculated using the Schrödinger equation?
I think I first heard of this complexity objection (which is of course something of a matter of taste in scientific theories, rather than a knockdown argument) from Daniel Gottesman, in a conversation at one of the Feynman Fests at the University of Maryland, although Antony Valentini (himself a Bohmian) has definitely stressed the ability of Bohmian mechanics to solve problems of high complexity, if one is allowed to violate the constraints that make it observationally indistinguishable from quantum theory. It is clear from rereading Bohm's 1952 papers that Bohm was excited about the physical possibility of going beyond these constraints, and thus beyond the limitations of standard quantum theory, if his theory was correct.

In fairness to Bohmianism, I should mention that in these papers Bohm suggests that the constraints that give standard quantum behavior may be an equilibrium, and in another paper he gives arguments in favor of this claim. Others have since taken up this line of argument and done more with it. I'm not familiar with the details. But the analogy with thermodynamics and statistical mechanics breaks down in at least one respect, that one can observe nonequilibrium phenomena, and processes of equilibration, with respect to standard thermodynamics, but nothing like this has so far been observed with respect to Bohmian quantum theory. (Of course that does not mean we shouldn't think harder, guided by Bohmian theory, about where such violations might be observed... I believe Valentini has suggested some possibilities in early-universe physics.)

A question about measurement in Bohmian quantum mechanics

Posted on by

I was disturbed by aspects of Craig Callender's post "Nothing to see here," on the uncertainty principle, in the New York Times' online philosophy blog "The Stone," and I'm pondering a response, which I hope to post here soon.  But in the process of pondering, some questions have arisen which I'd like to know the answers to.  Here are a couple:

Callender thinks it is important that quantum theory be formulated in a way that does not posit measurement as fundamental.  In particular he discusses the Bohmian variant of quantum theory (which I might prefer to describe as an alternative theory) as one of several possibilities for doing so.  In this theory, he claims,

Uncertainty still exists. The laws of motion of this theory imply that one can’t know everything, for example, that no perfectly accurate measurement of the particle’s velocity exists. This is still surprising and nonclassical, yes, but the limitation to our knowledge is only temporary. It’s perfectly compatible with the uncertainty principle as it functions in this theory that I measure position exactly and then later calculate the system’s velocity exactly.

While I've read Bohm's and Bell's papers on the subject, and some others, it's been a long time in most cases, and this theory is not something I consider very promising as physics even though it is important as an illustration of what can be done to recover quantum phenomena in a somewhat classical theory (and of the weird properties one can end up with when one tries to do so).  So I don't work with it routinely.  And so I'd like to ask anyone, preferably more expert than I am in technical aspects of the theory, though not necessarily a de Broglie-Bohm adherent, who can help me understand the above claims, in technical or non-technical terms, to chime in in the comments section.

I have a few specific questions.  It's my impression that in this theory, a "measurement of position" does not measure the pre-existing value of the variable called, in the theory, "position".  That is, if one considers a single trajectory in phase space (position and momentum, over time), entering an apparatus described as a "position measurement apparatus", that apparatus does not necessarily end up pointing to, approximately, the position of the particle when it entered the apparatus.

Question 1:  Is that correct?

A little more discussion of Question 1.  On my understanding, what is claimed is, rather, something like: that if one has a probability distribution over particle positions and momenta and a "pilot wave" (quantum wave function) whose squared amplitude agrees with these distributions (is this required in both position and momentum space? I'm guessing so), then the probability (calculated using the distribution over initial positions and momenta, and the deterministic "laws of motion" by which these interact with the "pilot wave" and the apparatus) for the apparatus to end up showing position in a given range, is the same as the integral of the squared modulus of the wavefunction, in the position representation, over that range.  Prima facie, this could be achieved in ways other than having the measurement reading being perfectly correlated with the initial position on a given trajectory, and my guess is that in fact it is not achieved in that way in the theory.    If that were so it seems like the correlation should hold whatever the pilot wave is.  Now, perhaps that's not a problem, but it makes the pilot wave feel a bit superfluous to me, and I know that it's not, in this theory.  My sense is that what happens is more like:  whatever the initial position is, the pilot wave guides it to some---definite, of course---different final position, but when the initial distribution is given by the squared modulus of the pilot wave itself, then the distribution of final positions is given by the squared modulus of the (initial, I guess) pilot wave.

But if the answer to question 1 is "Yes", I have trouble understanding what Callender means by "I measure position exactly".  Also, regardless of the answer to Question 1, either there is a subtle distinction being made between measuring "perfectly accurately" and measuring "exactly" (in which case I'd like to know what the distinction is), or these sentences need to be reformulated more carefully.  Not trying to do a gotcha on Callender here, just trying to understand the claim, and de Broglie Bohm.

My second question relates to Callender's statement that:

It’s perfectly compatible with the uncertainty principle as it functions in this theory that I measure position exactly and then later calculate the system’s velocity exactly

Question 2: How does this way of ascertaining the system's velocity differ from the sort of "direct measurement" that is, presumably, subject to the uncertainty principle? I'm guessing that by the time one has enough information (possibly about further positions?) to calculate what the velocity was, one can't do with it the sorts of things that one could have done if one had known the position and velocity simultaneously.  But this depends greatly on what it would mean to "have known" the position and/or velocity, which --- especially if the answer to Question 1 was "Yes"--- seems a rather subtle matter.

So, physicists and other readers knowledgeable on these matters (if any such exist), your replies with explanations, or links to explanations, of these points would be greatly appreciated.  And even if you don't know the answers, but know de Broglie-Bohm well on a technical level... let's figure this out!  (My guess is that it's well known, and indeed that the answer to Question 1 in particular is among the most basic things one learns about this interpretation...)

Rorem on Bizet... and Gedda and Vanzo in "Je crois entendre encore"

Posted on by

Reading Ned Rorem's essay on Bizet's Carmen, I can understand how he can say, even while admitting that Carmen is a "chef d'oeuvre", that it "does not make my mouth water. (No offense, neither does Schubert.) I like everything about it but it. .... One can admit to the fact of, and even cheer, certain universal marvels without needing them, while in the private heart one elevates to Parnassus lesser works which merely (merely?) satisfy."  I'm not sure I'd join him in this, although it's true I haven't sought out the opera very actively, except for a recent listen to the unusual recording (Prêtre conducting) with Callas late in her career.   The movie with Plácido Domingo as José, though, is memorable even though I haven't seen it since its first release, several decades ago now.  But I definitely can't join Rorem in his opinion that "There are no flukes in art.  Yet Carmen is a fluke.  Its high quality, if not its style, is incongruous in Bizet's catalogue."  Bizet was in his 37th year when he died of a heart attack (three months after the premiere of Carmen).  It's just as likely that Carmen was Bizet breaking through, not all that late, to his full power as composer, a power amply presaged by the best moments in his early work.  Rorem says that "Even his best works---the young Symphony, Jeux d'Enfants, parts of The Pearl Fishers---are in the salonistic genre of his period."  Well, I'm motivated to get to know the Symphony and Jeux by this.  And I suppose there is something salonistic, perhaps occasionally slightly cheesy, in parts of the Pearl Fishers.  More seriously, not all of Pearl Fishers is inspired...although good, transparent conducting, well recorded like Dervaux' in the 1960 Paris studio version with Nicolai Gedda as Nadir, Charles Blanc as Zurga, and Janine Micheau as Leila reveals plenty of beauty throughout.  And I guess my taste is somewhat more tolerant than Rorem's for the "salonistic" in music, and especially French music where Rorem admits "my taste buds crave a Frenchness that did not yet exist, a longing for the almost edible sadness that resides in the sharp seventh recipes of Debussy and Ravel."  Well, I find these delectable too (as I do the recipes with ninths thrown in, or a dash of pentatonicism), although not only when sadness is at issue.  But I sense that the modal moods of Debussy and Ravel show light, but important, traces of nineteenth-century "salonistic" influences, even, I think, of the Bizet of Carmen and the Pearl Fishers. I'll admit that the prismatic aperçus and pellucid vistas of Debussy and Ravel usually surpass the slightly overripe, though oh-so-tasty, sensuality of a Reynaldo Hahn, or even of Fauré in his early songs---Aprés un Rêve, which I do love, being just the most obvious example.  The great thing, of course, is that we don't need to choose between the two, except as a matter of allocating limited listening time---we can have both.

With the best of Pearl Fishers, though, Bizet makes it clear that Carmen was no fluke, but just the first mature fruit of a genius that was already perfectly evident, indeed in places perfectly realized, in the earlier work.  The tenor-baritone duet Au fond du temple saint, and the tenor romance Je crois entendre encore, both from Act I, are generally considered the greatest moments of Pearl Fishers.  Au fond is indeed wonderful, but after repeated listening to many versions of both (as they both do make my mouth water), I think Je crois is the greater of the two.   Salonistic, sentimental, whatever, it is the kind of aria that most composers can only dream of writing, nearly divine in its perfection and beauty.

The two singers I like best in this are Alain Vanzo and Nicolai Gedda.  I've linked some Youtubes of Vanzo singing this earlier, but I'll link another below.  Vanzo, in the second video below, uses the voix mixte to great effect, with a certain airiness in his timbre where Gedda's, in the first video, is smoother, probably a bit louder and more standardly operatic, with great clarity and perhaps slightly more control (they both have good control, though, and shape the line beautifully).  The last video, however, is of a 1953 recital performance by Gedda, whose timbre here is much closer to Vanzo's, and perhaps a bit more expressive too.  As is common in recital (for those uncommon singers who can do it), Gedda takes the final line that in the operatic arrangement is allotted to the English horn (over the singer's held note), going up to a piano high C.  (Vanzo can do this beautifully too, as he does in the video linked in an earlier post.)

Gedda, 1960:

Vanzo:

Gedda, 1953 recital:

Thomas Mapfumo--- Los Alamos 2012, Festivo 2013 (video)

Posted on by

Last summer Zimbabwean musician Thomas Mapfumo (currently in exile as a critic of the Mugabe government) played one of the free outdoor Gordon's Concerts in Los Alamos, next to Ashley Pond.  The concerts are organized by Russ Gordon, and funded by the County and by local individual, institutional, and business donors.  Russ does an incredible job getting unbelievable talent, often somewhat lesser-known but almost always excellent.  Mapfumo, though, is not lesser-known, but rather world-renowned.  Amazing that we got him all to ourselves for a night of dancing to his complex, catchy polyrhythmic Zimbabwean music, heavily influenced by traditional Shona mbira music and all kinds of "afropop".  His lineup featured a crack horn section.  At the time it was tenor sax and, if I remember rightly, a trumpeter.  Just by looking at the video below, I recognize the sax player, although here he's playing alto sax, and his fellow horn section member is on trombone.

Very worthwhile 2013 concert video follows.  First piece sounds somewhat uptempo, hilife-influenced to me.  Second one (starting around 9'30) a bit slower, more hypnotic, still rhythmically complex.  And so forth.  Excellent stuff.  The horn section had more impact in person last summer...a really powerful combination with the mbira-like guitar and keyboard parts.  But this is a great set too:

 

 

Trader Joe's Wine Roundup 7/1/2013

Posted on by

No, the Wine Roundup is not some event Trader Joe's sponsors out in its Wild West locations like Santa Fe, it's just me rounding up some empties I wanted to post about before chucking them.

Chateau Haut Sorillon, Bordeaux Supérieur, 2010. Tasty and medium bodied, not complex but fairly balanced and without any of the characteristics that can be offputting in inexpensive Bordeaux. Excellent with tomato and pasta salad and with bread and cheese (Manchego and Cambozola) while picnicking at St. John's College's Wednesday night Music on the Hill. Kind of the straight-ahead hard bop of wine...gets the job done in a satisfying but not ultra-flashy or revelatory way, like one of your more your basic Hank Mobley or Lee Morgan cuts. Very good value at 8 bucks.  Lessay 8 points or so on my 10 point scale that goes to 11.  85 on a Parkeresque scale.

Looks like one NatashaZ93 is keeping far better track than I have time or capacity to, of the TJ value parade...here's her take on the Haut S.

Panilonco Carménère DOC Colchagua (Chile) 2011 Reserva.  I liked the 2009.  I like this too, maybe even better.  Uncomplicated, good varietal flavor, good plush fruitiness and a bit of green tomatoey acidity (but not too much).  Yup.  This'll set you back all of 4 bucks.  I'd say 7.5 points... 83 on a Parkerish scale.

Bois de Lamothe AOC Côtes de Duras 2010  Merlot Cabernet Sauvignon.  Good stuff.  Along the same lines as the Haut  Sorillon (very Bordeaux like) but a bit more austere and rustic, and possibly a hint of something funky in the nose but not enough to be offputting.  Good flavors of  blackberry, a little vegetality to add complexity, maybe even a bit of tarriness.  Another 4 buck wonder!  If one must rate, I'd say the same as above... 7.5, or 83 Parkeresque points.  No, not that Parker... this is more like early Jackie McLean.

I blended together the last glass or so worth of the Panilonco and the Lamothe after they'd been sitting in the fridge for close on a week...it made quite a good blend, possibly even better than each wine alone.  Panilonco added lushness, the Lamothe restrained the Carménère's fruitiness a bit.

Terredora di Paola Irpinia Falanghina 2012

Posted on by

Figured I should get a few quick comments out on some wines while still timely... here's the first

The 2012 Irpinia (DOC) Falanghina (grape) from Terredora di Paolo, $15 at Susan's Fine Wines and Spirits in Santa Fe, was excellent and unusual. Just the sort of thing I was hoping for in an unfamiliar Italian white. Strong flavors, a little bit of almond and lemon and maybe minerality, typically Italian hint of bitterness, a nice smooth but not glyceriny feel in the mouth, a long finish.   Surprisingly high in alcohol (14%) but able to stand up to it with concentration of flavor and freshness. Not something I would age, not super super complex, but not one-dimensional either.  Great clarity of flavor, vigorous but pretty balanced. Not inexpensive but a very fair price for the quality...you are unlikely to get such concentrated flavor combined with balance, even elegance, for less.  I wasn't familiar with the grape variety, a local grape of Campania, the Italian region in which Naples is situated. I'd never been to Susan's before, although I'd read and heard good things, so I checked it out and was impressed by what looks like a carefully chosen and interesting selection. This wine was recommended by Susan herself; based on it, I'll be going back for more of her recommendations.

Catchy and free... St. Etienne "Lose That Girl"

Posted on by

This post is just to point out that you can download a free mp3 of St. Etienne's catchy "Lose That Girl" from Sub Pop here.  (The link is under "Listen", 2nd column from the left.) I am not familiar with this band's oeuvre in detail but I like this tune.  They do have an official Youtube channel, where you can investigate cheery proto-britpop (with various amounts of electronic dance beats admixed) from the early 90s like 1992's Avenue:

or check out their more recent doings (that seem to involve more insistent, but lightfooted, electronic dance beats), like Tonight

Essential listening: Alicia de Larrocha plays Granados

Posted on by

Alicia de Larrocha plays Enrique Granados' piano music on RCA Red Seal (BMG) CD 09026-6814-2.  Music and performance are perfection.  Can't imagine it done better.  Truly essential listening.  The musical equivalent of a Catalonian monastery, a Tuscan hilltop town, a Campanian fishing village.  Understated, picturesque, quotidian, unforgettable.

Essential listening: the Guarneri play Janácek

Posted on by

On a 1998 Philips CD, number 456 574-2, the Guarneri quartet plays both of Leoš Janácek's string quartets:  the 1923 "Kreutzer Sonata" and the 1928 "Intimate Letters".  This is wonderful music, tonal but not staidly so, beautifully played (in 1996) by the Guarneri.  Plenty of melodic and harmonic beauty, deeply felt but not sloppy or over-the-top.  Excellent recording captures the rosiny, woody aspects of string tone, and a bit of astringence but not too much.  Good acoustic ambience...fairly reverberant, but the sound is very clear.  Possibly more closely-miked than is completely realistic, but that gives a clear insight into the separate lines without sounding glaringly close up.  I don't know the other recordings of this piece, so can't comment on which others one might entertain in addition to, or instead of, this one.  Doesn't really matter:  this is essential music, beautifully rendered.  I will say no more except that every music lover would be well-advised to listen to these pieces, in this or some equally good recording if one exists, and to go hear them live if the opportunity arises.

 

Sorry for the lack of correct Czech diacritical marks.  A computing issue I will work on.