Not the Leonard Cohen song. The Happy Mondays, from Madchester Rave On:
Lunch at Perimeter: Rice-wrapped Seabass with Puy Lentils.
Perimeter's bistro is amazing. The rice-wrapped seabass with Puy lentils I had yesterday at lunch was perfection. Nice, thick piece of fish, cooked perfectly. Flaky. Firm. Moist. Flavorful. Swathed in a rice wrapper and lightly browned, ending up covered in a crisp, savory golden sheath. Thin slivers of red and yellow peppers and suchlike veggies encased with the fish. The whole atop a generous bed of tiny, dark, earthy, intense Puy lentils, larded with and accompanied by more bits and slivers of veggies---carrot, more peppers, and so on. A drizzle of excellent olive oil. Karla, Steve, Frank, and the rest of the chefs and kitchen staff at PI get a big salute, or in Japanese style, a deep bow of acknowledgment, for this and many other unfussy but elegant, intense, and satisfying creations. Food like this relaxes and rejuvenates mind and body. I think we all work better---prove better theorems, achieve better philosophical insights, find more efficient ways to make the institute run or keep the building in good shape, and so forth, after a meal like this. Not that that's the point---like a piece of music, a painting, or a good theorem, such a dish is its own best reason for being.
Vijay Vazirani thinks we should look for combinatorial algorithms for convex programs
Just a link to Vazirani's guest post on Noam Nisan's blog Algorithmic Game Theory, which seems to relate to my interest in convex sets with beautiful structure. (Homogeneous self-dual cones, like the positive semidefinite matrices (semidefinite programming) or the positive orthant (linear programming); just plain homogeneous cones; hyperbolicity cones...; just plain self-dual cones; weakly self-dual cones (ones isomorphic to their dual, but for which no inner product on the space can make the dual (defined according to said inner product) equal to the cone itself), etc...). And a thought, perhaps misguided: isn't a crucial ingredient of an efficient algorithm for a convex program usually something like an efficient algorithm for something like: determining membership in the convex set, or calculating a nice barrier function for the set? And doesn't the ability to do that usually depend on the set (and/or the cone it generates) having a "nice" structure? Perhaps the detailed properties of this structure bears some relation to the "combinatorial" structure of algorithms like the Ford-Fulkerson algorithm for max-flow? Or perhaps particular problems have additional structure that isn't being captured in a typical convex formulation. I'm no expert here (and have indeed forgotten what the Ford-Fulkerson algorithm is, though I think I once read about it in a book by Vazirani). This post is primarily to remind myself to look at this more closely---and to link to Vazirani's, which seems worth of attention.
To my mind, a 15th gold medal olympic performance for Canada---k.d. lang, Hallelujah
One amazing thing about this olympics was that most of the athletes' gold medal performances were as enthralling and moving, in their distinct ways, as k. d. lang singing fellow-Canadian Leonard Cohen's Hallelujah at the opening ceremonies.
Liveblogging Canadian gold-medal 3-2 hockey win celebration from uptown Waterloo Ontario
The horns and cheers are sounding in my house a block off the main street (King street) of uptown Waterloo. I watched the end of the US-Canada hockey game in a pub, the Fox and Fiddle, on King street and it was a hard-fought thriller. I'm happy for Canada, and they're sure as heck happy! The US team fought hard and has nothing to be ashamed of---but you could see the disappointment in their faces afterward, though they were absolutely sportsmanlike about it.
King street near the major pubs is lined with people hugging each other, high-fiving, waving canadian flags, and stopping passing motorists to high-five them as well. After a Candian lead of 2-1 held for a long time, the US, which had been playing strongly and getting plenty of time with the puck, made a tieing goal with about 20 seconds left. In a really hard-fought overtime, Canada sunk a sudden-death goal for the gold. With that medal, they now have the most gold medals any country has won in a single winter olympics, said the commentators on CBC TV.
There was a lot of spirit in the pub, and I realized I was dressed in black, grey and blue from head to toe---not a spot of red except on my red, grey, and blue hat. (Or should that be tuque?) No issues, though---I am not a hugely vocal sports fan and don't normally watch hockey---though somehow the guy who was going 'round hugging everyone in the pub took a look and gave me a miss. I walked up and down King street to check out the scene, and ended up having to high-five a few people and clap one person on the back, all with a "Congratulations!" which presumably marked me as not Canadian. (A Canadian would yell "Canada, yeeeaaaaaaaah!!!"., as about five hundred are doing a block or two away right now.)
I did see one ambulance turn the corner onto King, lights flashing. Keep it safe out there, guys and gals. Don't drink and drive, don't get into fast traffic, etc... (Fifteen minutes after the victory, after the medal ceremony, a group in the pub raised a chant of "Let's get wasted!".)
I had a pint of Molson's Canadian Lager during the overtime. The drink of the Canadian women's hockey team, it was clear, smooth, and tasty, and really hit the spot. No cigars today, though---although I suppose up here you can get real Cubans. (Now there would be a provocative way to celebrate a US win!)
I'm glad it was a really hard-fought game, with everyone playing their best, and I don't think anybody should feel bad about their performance. Great job all around, and a smashing finish for the Canadians to a great olympics!
It's getting louder out there. Hopefully I can find my camera and post some pics of the celebration.
Edit: didn't find my camera, but Youtubers provide more than enough flavor of the scene:
Interesting links for Sunday 2/28/2010: political economy of protectionism, complexity of the theory of the reals, subgroups of SU(N), and how to write mathematics.
Interesting-looking bit of political economy research. They propose that sectors employing lower-earning workers more intensively are receive relatively more trade protection, based on research in the US and China, and apparently attempt to differentiate between the contributions of envy and altruism to this effect. Also, presumably, compare it to theories where amount of protection depends primarily on the resources available to an industry to help secure it. NBER charges five bucks (OK, that beats Springer journals hands-down, but still) to download, so unless PI gets a subscription, looks like I'm not reading it. What is with charging money for working papers!? Can't we get these economists on the arXiv???
Proving that Proving is Hard. Computer scientist Dick Lipton gives a beautiful introduction to work by Fischer and Rabin on the computational complexity of the formal first-order theory of the real numbers. As Lipton explains, Alfred Tarski showed that this theory is complete---that every well-formed statement in the language of the theory can either be proved, or be disproved, from the axioms of the theory. Fischer and Rabin investigated how hard it can be to prove statements in the theory. According to Lipton, they showed that it's (worst-case) exponentially hard: there is a positive constant  such that there are true sentences of the theory, of length shorter than
such that there are true sentences of the theory, of length shorter than 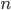 , whose shortest proof has length at least
, whose shortest proof has length at least 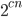 . (I'd guess what's meant is that they show this holds for all large enough
. (I'd guess what's meant is that they show this holds for all large enough 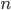 , or at least for an infinite set of
, or at least for an infinite set of 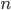 .)
.)
Quantifier elimination---the method of deciding statements in the theory of the reals, used by Tarski in his decidability proof---has, at least theoretically, applications in optimization, which I hope to delve into in a future post.
A nice, probably not-too-easy (for me) and not-too-hard problem in group theory from my colleague Alberto Montina: is 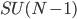 a subgroup of
a subgroup of 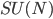 of maximal dimension (as a manifold) and are there any others.
of maximal dimension (as a manifold) and are there any others.
Paul Halmos, How to Write Mathematics.
Print-On-Demand publishing: will it allow academics to compete with major publishers?
Since I'm thinking of writing a scholarly book or two, I wonder whether print-on-demand publishing houses, combined with outlets like Amazon, allow academics to effectively compete directly with the more usual academic publishers like Springer, Cambridge UP, Oxford UP, etc...? I've recently noticed that in ordering new books from all three of these publishers, I've frequently been sent what look like print-on-demand editions. Here's a bit on Springer's POD activities. To take one recent purchase, Faraut and Koranyi's Analysis on Symmetric Cones, Oxford, is now print-on-demand, and they're still charging $200 for it. It's adequate, but much less attractive than the original edition which has the trademark Oxford deep-blue cloth-covered boards, with nicely finished paper (perhaps excessively sized, even) and extremely crisp type. The print-on-demand edition is on paper that's not as nice, an almost inkjet-printed appearance where the edges of the characters are just not crisp enough for my taste, and the boards are thick, covered with something glossy, and more prone to warp outward so the book doesn't quite close firmly. Springer and Cambridge POD books are similar. It's a little more like you LaTeX'd something, printed it out two-pages-to-a-sheet, cut the sheets in half and glued them into a binding. (Except maybe your average laser printer would produce sharper results---I'd need to do a direct comparison.) This is quite serviceable for the right price, for usable math books, but $200 (I was able to find it for less, but still an outrageously high price) seems ridiculous. But if academics were able to publish their works this way, sell for $40-65, deduct the cost of printing (about which I'm quite curious), do a little yearly accounting and extra business at tax time, and pocket the rest, it might be a much better deal than publishing through a major house. I suspect that for a good academic work, reputation developed through citations and online access (one could make the book available chapter-by-chaper for free, if desired) might work almost as well as the publicity provided by an academic or corporate publisher. The major issue might be library purchases, I'm guessing. Anybody out there have any experience or ideas with this?
More info: Amazon's POD printing and distribution unit, Createspace (Springer's US partner) has an expanded distribution plan claimed to wholesale books to libraries and bookstores. Cambridge has partnered with LightningSource.
Here's a video of the Espresso Book Machine, for producing paperback books at or near the point of sale, in action:
Here's Amazon's "Pro Plan" at their CreateSpace. The combination of the terminology "royalties" for the money you get, and "self-publishing", seems, technically, contradictory. Royalties are paid by a publisher for the right to publish and sell your book; if you were actually self-publishing, you would be hiring Amazon/Createspace to print your book, and do some of its distribution and sales, but what you keep would be profit, not royalties. So I'm curious which it actually is, in their case. Anyway, you seem to get about 43% of the list price on sales through Amazon, 23% on their Expanded Distribution Channel (to libraries, bookstores, and "certified resellers" at, presumably, wholesale prices, although maybe not since Amazon labels the entire difference between your share and list price "Our Share"), and 63% through something called an eStore (which is presumably an outlet at your own website, linked to Amazon; more investigation warranted). Those are on a $16 book; on a $45, 320 page book with black and white interior, it looks like 30% through the EDC, 50% through Amazon, and 70% through your eStore. I'm guessing this is for a paperback.
So, quite a bit better than the standard academic press royalty which I believe is something like 7% or so, but still, through the expanded distribution channel, not that hefty.
How does one prove that domains of positivity of symmetric nondegenerate bilinear forms are self-dual cones?
On mathoverflow, I've asked how one proves that domains of positivity of symmetric nondegenerate bilinear forms on real vector spaces are self-dual cones. A bilinear form on a real vector space 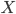 is just a map
is just a map 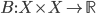 that is linear in each argument. (In other words, if you fix
that is linear in each argument. (In other words, if you fix 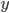 , the function
, the function 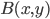 that takes
that takes 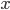 to
to 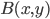 is linear, and similarly if you fix the other argument.) It's called nondegenerate if the only
is linear, and similarly if you fix the other argument.) It's called nondegenerate if the only 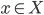 such that
such that 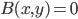 for all
for all 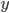 , is
, is 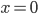 . And, of course, it's symmetric if for all
. And, of course, it's symmetric if for all 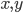 ,
, 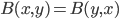 .
.
A closed domain of positivity of such a form is a maximal set 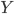 such that
such that 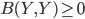 . Maximal means maximal in the ordering of sets by containment, i.e.
. Maximal means maximal in the ordering of sets by containment, i.e. 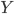 is not contained in any other set
is not contained in any other set 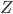 satisfying
satisfying 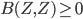 . This notion was introduced, or at least used, by Max Koecher in the late 1950s, in work that led to the celebrated result, published in 1958 in "The Geodesics of Domains of Positivity" (well, actually, "Die Geodatische von Positivitatsbereichen" (Mathematische Annalen 135 (1958), pp. 192--202)), that homogeneous self-dual cones in finite dimension are precisely the cones of squares in finite-dimensional formally real (aka Euclidean) Jordan algebras. Indeed, probably the very interpretation of the main result of that paper as concerning homogeneous self-dual cones relies on the identification of domains of positivity with self-dual cones that I'm looking for a proof of.
. This notion was introduced, or at least used, by Max Koecher in the late 1950s, in work that led to the celebrated result, published in 1958 in "The Geodesics of Domains of Positivity" (well, actually, "Die Geodatische von Positivitatsbereichen" (Mathematische Annalen 135 (1958), pp. 192--202)), that homogeneous self-dual cones in finite dimension are precisely the cones of squares in finite-dimensional formally real (aka Euclidean) Jordan algebras. Indeed, probably the very interpretation of the main result of that paper as concerning homogeneous self-dual cones relies on the identification of domains of positivity with self-dual cones that I'm looking for a proof of.
If the form were positive semidefinite, i.e. 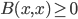 for all
for all 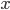 (which implies symmetry) then a domain of positivity for would clearly be a self-dual cone. This is practically the definition of a self-dual cone. The dual of a cone in a real inner product space is the set of all vectors
(which implies symmetry) then a domain of positivity for would clearly be a self-dual cone. This is practically the definition of a self-dual cone. The dual of a cone in a real inner product space is the set of all vectors 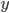 whose inner product with everything in the cone is nonnegative---and the definition of an inner product on a real vector space is that it's a nondegenerate positive semidefinite bilinear form. A self-dual cone is one that's equal to its dual cone.
whose inner product with everything in the cone is nonnegative---and the definition of an inner product on a real vector space is that it's a nondegenerate positive semidefinite bilinear form. A self-dual cone is one that's equal to its dual cone.
For our definition of domain of positivity, the form was required only to be symmetric, not necessarily also positive semidefinite. Nevertheless, according to things I've read, its domains of positivity are self-dual cones. These domains are not necessarily unique, of course, although they are maximal, i.e. no one of them contains another). Although I have a vague recollection of having seen a proof that they are self-dual, I haven't been able to find the paper or come up with a proof.
It's easy to prove that such a domain is a pointed, convex, closed cone. A natural way to prove that it is a self-dual cone would be to exhibit a positive semidefinite form 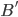 , depending on
, depending on 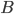 and possibly also on
and possibly also on 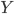 , such that
, such that 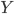 is a domain of positivity of
is a domain of positivity of 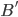 . An idea for how to do this involves the fact that such a form can be diagonalized: we can find a basis
. An idea for how to do this involves the fact that such a form can be diagonalized: we can find a basis 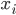 for the vector space such that the matrix with elements
for the vector space such that the matrix with elements 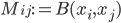 is diagonal, with diagonal elements
is diagonal, with diagonal elements 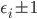 . The number of
. The number of  signs on the diagonal is the signature of the form. A natural candidate for
signs on the diagonal is the signature of the form. A natural candidate for 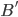 is the Euclidean inner product
is the Euclidean inner product 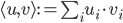 in the basis
in the basis 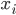 (i.e
(i.e 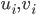 are the components of
are the components of 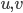 in this basis). That is, we just change the
in this basis). That is, we just change the 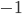 's to
's to 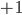 's in the diagonal form of
's in the diagonal form of 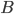 .
.
Nondegenerate symmetric bilinear forms are interesting for a variety of reasons. One of them is that they are closely related to the metric structure on a pseudo-Riemannian manifold. Something like the following is true: you specify such a form at each point of the manifold, in such a way that the forms at the various points are nicely related to each other, and you've specified the geometric structure of a pseudo-Riemannian manifold. (One restriction here, I believe, is that the signature of the forms has to be the same everywhere; the forms also need to vary somewhat smoothly, in a manner I should look up and summarize, but not now.) For example, in the general relativistic description of spacetime, the spacetime manifold has signature 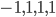 . Or
. Or 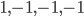 ; people use different conventions. I'm attracted to
; people use different conventions. I'm attracted to 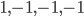 , because the odd-one-out corresponds in relativity theory to time, and this way, the forward and backward light cones are the (only!) domains of positivity for the form. I.e. the form is
, because the odd-one-out corresponds in relativity theory to time, and this way, the forward and backward light cones are the (only!) domains of positivity for the form. I.e. the form is 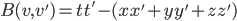 ; we have
; we have 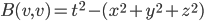 (here
(here 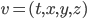 , etc...). Interestingly, with the other choice of signature, the domains of positivity consist of spacelike vectors, and there is a continuum of them. To get a picture of what's going on, consider one time and two space dimensions, with signature
, etc...). Interestingly, with the other choice of signature, the domains of positivity consist of spacelike vectors, and there is a continuum of them. To get a picture of what's going on, consider one time and two space dimensions, with signature 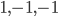 . You can visualize this in
. You can visualize this in 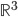 , with the vertical
, with the vertical 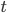 axis as time (associated with the
axis as time (associated with the 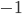 diagonal element of the form) and the horizontal
diagonal element of the form) and the horizontal 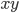 planes for constant time
planes for constant time 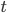 as a spacelike plane. If you rotate the 45 degree line between
as a spacelike plane. If you rotate the 45 degree line between 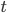 and say the
and say the 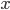 axis, around the
axis, around the 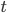 axis, you get the boundary of a double cone, the forward and backward light cones. But similar cones pointing along any ray in the
axis, you get the boundary of a double cone, the forward and backward light cones. But similar cones pointing along any ray in the 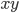 plane are clearly domains of positivity for the form. I suspect lots of other cones---basically, any self-dual cone you can fit into the "conic doughnut" that is the closed complement of the double light-cone, i.e. into the spacelike (and null) vectors, are also domains of positivity for this form.
plane are clearly domains of positivity for the form. I suspect lots of other cones---basically, any self-dual cone you can fit into the "conic doughnut" that is the closed complement of the double light-cone, i.e. into the spacelike (and null) vectors, are also domains of positivity for this form.
My main reason for interest in the problem isn't pseudo-Riemannian geometry, however. More on the main reason later. (It has to do with the Koecher result cited above).
If you found this problem first on mathoverflow, and you have the answer, please post your answer there, and link to it here if you feel like it; if you encountered it first here, please post the answer here indicating you encountered the problem here, and it would be nice if you'd also post it on mathoverflow indicating you found it on my blog. We can have a little race between we happy few who read this blog, and the overflowing mathematicians. I know who I'm betting on---your mission, readers, should you choose to accept it, and should any of you actually exist, is to prove me wrong!
(Thanks to Will Jagy, of MSRI, for noticing that I defined nondegeneracy wrong here at first: as requiring that the only 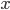 for which
for which 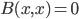 is
is 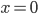 . This wrong definition, corrected above, of course says that the form has no nontrivial "isotropic" or "null" vectors (ones for which
. This wrong definition, corrected above, of course says that the form has no nontrivial "isotropic" or "null" vectors (ones for which 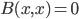 ). And we certainly don't want to assume that! Sorry about the slip-up, which I dont think affected anything else in the post.)
). And we certainly don't want to assume that! Sorry about the slip-up, which I dont think affected anything else in the post.)
Smash (well, hope the U.K. has the good sense to radically revise) the British libel laws!
I wasn't planning another post in the "Smash" series for awhile, but this just had to be titled so. When I followed this up from Matt Leifer's site, I just had to draw attention to it. British science writer Simon Singh is being sued for libel by the British Chiropractic association for calling some of their treatments bogus. Part of a broader problem of British libel laws chilling free speech, including discussion of so-called Islamist extremism in Britain, as discussed in this Daily Mail article. More links at "sense about science". Matt's post is from last August, so hopefully something strong has been done about this by now; I'll have to look into it. This could seriously damage Britain if something isn't done about it.
Economics readings: Interview with Eugene Fama; consumption and healthcare
Amazing interview with Eugene Fama who doesn't believe the present crisis is due to the bursting of a bubble in housing: "That’s where economics has always broken down. We don’t know what causes recessions. Now, I’m not a macroeconomist so I don’t feel bad about that. (Laughs again.) We’ve never known. Debates go on to this day about what caused the Great Depression. Economics is not very good at explaining swings in economic activity." (Link found on Paul Krugman's blog. )
And an interesting bit about consumption and healthcare from something called Left Business Observer (link found on Brad Delong's blog). The basic point is that of the six percentage point rise in what the national-income accounts categorize as consumption, as a share of GDP (from around 64 in the 80's to around 70% in 2007 and 2008), about four percentage points are in health care.
