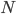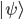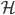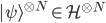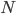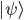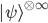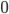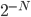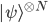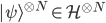Category Archives: Foundations of Quantum Theory

Myrvold on philosophy of physics and Hawking and Mlodinow

Posted on by

Since Hawking and Mlodinow's book "The Grand Design" (I keeping wanting to type "The Grand Illusion") is from 2010 (the stack of new copies I saw in the Harvard bookstore must have been remainders), there has, of course, been plenty of discussion of the "philosophy is dead" claim in the blogosphere.  Matthew Leifer kindly pointed me to a post by philosopher Wayne Myrvold in which Wayne tries to find what is reasonable in H & M's claim.  "The quest for the sorts of knowledge that Hawking and Mlodinow are talking has passed from people called philosophers to people called scientists, not because one group failed and had to pass on the torch, but because we started calling that quest “science,” rather than philosophy."  This is partly true, and my mention of "natural philosophy" was meant in part to allude to this, but let's look at the questions H&M pose again: "How can we understand the world in which we find ourselves?  How does the universe behave? What is the nature of reality?  Where did all this come from?  Did the universe need a creator?"  Inasmuch as philosophy of science is still a philosophical discipline, and not a part of science itself, the first question is still a major concern of what we call philosophy, even if scientists, obviously, have to address it at least tacitly because understanding the world is part of what they do.  As for the nature of reality, I suppose that depends in part upon what's meant by "the nature of reality".  But again, this is still a major concern of philosophy, even, perhaps especially, when reality is considered in its scientific aspect. What does it mean to say that the entities mentioned in scientific theories are real, when the theories they appear in get replaced by other theories, in which sometimes the old entities don't appear? It may be that physics will henceforth proveable to handle such questions with litle input from philosophers, but I don't think this is guaranteed. Inasmuch as science addresses the other two questions, about "where it all came from" and the existence of a creator, I also suspect that the broad point of view, and experience in the subtleties of the relevant concepts, of "analytic" philosophy, is still a valuable complement to science.  And then there are all the other questions that philosophy addresses.

Later, Myrvold says:

My own work consists, in part, of addressing the question, “What is the empirical success of quantum theory telling us about the world?”  This is a question that physicists don’t have to ask.  Much of the work done by physicists can proceed without an answer to this question.  Moreover, a case can be made, I think, that there have been moments in the development of quantum mechanics when progress was made by setting aside this question, at least temporarily.  But they can ask this question, and many of them do.  When they do so, they are engaged in philosophy of physics.

I guess physicists don't have to ask this, but many of them do. Plenty of scientists, in fact, think science is about finding out how the world is, beyond mere "empirical success". How "the way the world is" relates to "empirical success" is of course a classic philosophical question. But I think that often, when philosophers work on the question of what quantum theory tells us about the world, they are doing physics. This doesn't necessarily imply that Wayne is wrong that the physicists who ask that question are doing philosophy of physics. I take it rather to imply that this is where the unity of human thought that is suggested by terminology like calling science "natural philosophy" is evident. As I said in my first post on this subject, the people currently called "philosophers" have something to contribute, along with those called "physicists" and, perhaps especially, those who don't necessarily care what they are called.

I should point out that Wayne has a lot of good stuff to say following the paragraph I quoted, and I recommend reading it. (That's not to say I agree with all of it, of course.)

Philosophy is alive and well, whatever Hawking and Mlodinow may think.

Posted on by

Browsing in the Harvard Bookstore in Cambridge, MA last week, I looked at the first chapter of Stephen Hawking and Leonard Mlodinow's 2010 book "The Grand Design".  I was hit by this:

How can we understand the world in which we find ourselves?  How does the universe behave? What is the nature of reality?  Where did all this come from?  Did the universe need a creator? ...

Traditionally these are questions for philosophy, but philosophy is dead.  Philosophy has not kept up with modern developments in science, particularly physics.  Scientists have become the bearers of the torch of discovery in our quest for knowledge...

It's not only wrong, but even, I think, a bit arrogant to dismiss philosophy as dead.  Have these guys even read any contemporary philosophy of science, or mind? Have they been to any conferences on the philosophy of physics recently, like maybe New Directions in the Foundations of Physics?  Have they read Oxford philosopher David Wallace's recent work on the "many-worlds" interpretation of quantum theory which, although I'm quite out of sympathy with it, I think is genuine progress in understanding how one might make sense of --- and what are the obstacles to making sense of --- this view of quantum theory, which is subscribed to by some though certainly not all practicing physicists and cosmologists?   For that matter, are they not aware of the close interaction between some philosophers of science and cognitive scientists?  Or the attention that philosophers Paul and Patricia Churchland have paid to neuroscience (not that I agree with their views)?

So that's one point, that philosophy is hardly ignoring science.  I argue below (and the Wallace example already provides some evidence) that it has useful contributions to make to those parts of physics that deal with the kinds of big questions Hawking and Mlodinow raise.  But one other point needs to be made, which is that philosophy has much broader concerns, involving politics, morals, the good life, aesthetics, and social science, and in these areas too, it is alive and well and contributing.  I sincerely hope Hawking and Mlodinow don't think science is "the torch-bearer" there too, because although of course it is not irrelevant even there (probably no part of human thought can be declared a priori completely irrelevant to any other) that is a torch it is not capable of bearing.  If they really do think science is the torch-bearer here, I think they are contributing to the stunting of serious thought in these areas that are just as important to humanity as science, and indeed, to a stunted conception of humanity.

Now, I can dig that Hawking and Mlodinow, if they were to attend New Directions, might think that some of the stuff being done is not of interest.  In particular there is usually not that much philosophical discussion around string theory and M-theory, although quantum cosmology does come up on occasion.  Maybe they are not interested in the quantum foundations issues like "is the quantum state epistemic?" that come up frequently in New Directions.  I wouldn't be surprised, though, if there are other philosophy conferences that I don't attend where M-theory and quantum cosmology get much more attention.  Maybe they might think some of the stuff aimed at understanding the conceptual content of physical theories like general relativity that have been around for about 3/4 of a century, and comparing them to older theories like Newton's and heck maybe even Aristotle's, is pointless.  I'm referring to James Weatherall's excellent talk "Explaining intertial motion and the foundations of classical space-time theories".  (Here's a link to the paper the talk is based on.) But I'm speculating here; maybe they'd love it, realize that it's worth thinking about the conceptual structure of existing theories as one tries to incorporate what was good about them and go beyond (combining classical general relativistic space-time theory with quantum theory).  Or maybe they'd think it was all understood by physicists long ago, so while not pointless, just not contributing to progress.

Here's yet another point.  I frequently read or hear physicists spouting some methodological priniciple they got from some philosopher of science, often Karl Popper, or some view that is common in some branch of science but considered by philosophers to be quite problematic.  Sometimes it is used to good effect, sometimes used in a quite unsophisticated manner, with little consciousness of drawbacks and caveats well-known to philosophers.  For instance, some physicists freely use the frequency interpretation of probability with little or no understanding of its serious difficulties.  I have heard one of the world's most renowned cosmologists do this, and in response to my objections, dismiss the "Bayesian personalist" (sometimes called "subjective") view of probability by saying something along the lines of  "I'm not interested in betting, I'm interested in describing the world"), although I have also found that other reknowned cosmologists do have an active interest in the "personalist" interpretation of probabilty.  I suspect there are plenty of other places where, when physicists start addressing questions formerly thought of as "philosophical", or when they use philosophical principles or positions in formulating their physical theories (or their "interpretations" of such theories, which one might argue are really an essential part of the theories themselves), philosophers can help physicists avoid making both elementary and subtle philosophical (or perhaps we should just say conceptual) mistakes.

I have no problem with the view that the questions posed by Hawking and Mlodinow in the above quote are not just the province of philosophy, but require input from what used to be called "natural philosophy": science, including physics.  Nor do most contemporary philosophers!  But some of the careful conceptual analysis that philosophers have done, over the course of the twentieth century, of notions like truth, confirmation, induction, falsification, refutation, meaning, reality, perception, observation, theories, and so forth, is enormously relevant to any attempt to say what current physical theories, and speculations like M-theory, really mean for "the nature of physical reality".  It is cool that Hawking and Mlodinow are engaging in this attempt, and I plan to get their book out of the library and see what they have to say.  Perhaps I will even end up thinking that they have made enormous progress.  But I think they are foolish to dismiss the potential for contribution by philosophy to this enterprise.  Indeed, in their description on pages 6 and 7 of their philosophical approach, they say plenty of things that are easily found in the "analytic" philosophy of the latter part of the 20th century:  for example "we shall adopt an approach we call model-dependent realism.  it is based on the idea that our brains interpret the input from our sensory organs by making a model of the world.  When such a model is successful at explaining events, we tend to attribute to it, and to the elements and concepts that constitute it, the quality of reality or absolute truth.  But there may be different ways in which one could model the same physical situation, with each employing different fundamental elements and concepts.  If two such physical theories or models accurately predict the same events, one cannot be said to be more real than the other; rather, we are free to use whichever model is most convenient."  Well, philosophers have been discussing this possibility for decades.  Most usually, it is called "the underdetermination of theory by evidence." So, probably, have physicists; I am not sure in which community the possibility was first mooted, or whether it has occurred many times independently.  I'm looking forward to seeing what use Hawking and Mlodinow make of this possibility, but I consider it a strong possibility that the philosophers who have thought about it carefully may have something useful---useful to physics---to say about its use in physics, or in the application of physics to the big questions Hawking and Mlodinow aim to address.

Okay, enough rant.  I want physicists to think about the big questions; I hope Hawking and Mlodinow have genuine insight on them.  I'll report on that as I read their book.  But I really, really think it is miguided to dismiss the possibility that the field of philosophy as currently practiced has anything to contribute here.   And it goes beyond misguided to downright pernicious, and perhaps to a kind of narrow-minded science triumphalism which is, frankly, morally dangerous, to claim that "philosophy is dead" and that science is bearing its torch.  Let's hope that philosophers and physicsts continue to join forces where appropriate, as we do at New Directions, and indeed that they expand cooperative efforts, to deal with the big questions Hawking and Mlodinow want to address, to deal with other big questions, to deal with issues of how physics might best progress, how the insights of quantum theory and general relativistic spacetime theory can be combined into a more unified physical theory, and to understand better how physics and science fit into the broader picture of rational, and irrational, human activity.

Keep on splittin'

Posted on by

OK, I just had to copycat this link.  Via the Quantum Pontiff, Universe Splitter, a supposed new app for the iphone that supposedly hooks up to a quantum randomness generator, allowing you to condition your decisions on quantum randomness and ensure---if you believe in the Everett interpretation of quantum mechanics---that you can "have your cake and eat it too.  I hope this thing's for real, but unless it's just my lack of App savvy, Apple may not be buying the Everett interpretation.

Keep on Splittin

Keep on Splittin'

Foundational Questions in the Azores II: Limiting frequency arguments for the Born rule in Many Worlds

Posted on by

To take up where I left off, I was discussing the Many Worlds interpretation of quantum mechanics with Alan Guth at dinner the first night of the FQXi conference in the Azores.  If I understood correctly, he seemed to think that the Many Worlds (in the sense of One Hilbert Space---Many Mutually Orthogonal Subspaces in which macroscopically distinct things appear to be happening) interpretation was useful, perhaps needed, to deal with quantum effects in cosmology.  I asked him whether he though the question of justifying the Born probability rule in the MWI was an important issue, and whether he had any opinions on it.  (The Born rule,  introduced by Max Born early in the history of quantum theory, in a famous footnote in a paper of his, it says, rougly speaking,  that the probability of finding a given outcome of a quantum measurement is given by the square of the modulus ("absolute value" of a complex number) of the complex component of the state vector in the subspace corresponding to that outcome.)  He advocated the Farhi-Gutmann version of an argument going back to James Hartle in 1965, and perhaps earlier to Finkelstein.  In his telling, the idea is that as long as one is willing to "neglect components of the wavefunction with vanishingly small modulus", the fact that when one makes repetitions of the same measurement on the same state of Hilbert space (prepared again for each measurement) the state is represented by a tensor products implies that the state is (except for a negligible component) in a subspace in which frequencies are close to those given by the Born rule---approaching the Born frequencies ever more closely as gets larger.

Hopefully I've rendered what Guth had in mind reasonably well---we didn't formalize things on a napkin or anything.  In some versions of this argument, one actually goes to an infinite tensor product Hilbert space, and the claim is made that the vector corresponding to an infinite number of independent preparations of ---call it if you like---just is an eigenstate of a "relative frequency operator" on this infinite tensor product Hilbert space, with eigenvalue equal to the Born probabilities.  I believe that's the claim of the Farhi and Gutmann paper --- but Caves and Schack claim it's incorrect.  Then---by the "eigenvalue-eigenstate link", which is a "minimalist" interpretation of the state vector's relation to actual observational outcomes, saying that if a state actually has a definite eigenvalue for some observable, than the outcome corresponding to that eigenvalue is actual (perhaps this can be thought of as assigning probabilities and to outcome subspaces in which the state has zero component, or in which the state is contained, respectively)---one concludes that the Born rule probabilities are the only ones that give the correct relative frequencies, in the infinite limit.

Whether or not the claim about the infinite state being an eigenstate of relative frequency is correct, I'm suspicious of arguments that require an actualized infinity---I try to understand them by understanding the actual limit as summarizing---albeit with some quantitative details of rates of convergence suppressed---how things "can be made to look in large finite cases"---i.e., the 's and 's rule my understanding.  So---without having looked at the Farhi and Gutmann paper recently, however---let's think about this; it's something I've thought about before.  Basically, it seems to me incorrect to claim that the state approaches an eigenstate of a sharp relative frequency operator---although the expectation value of its relative frequency list approaches the Born rule probabilities, as grows it remains in a superposition of eigenstates of the -th relative frequency operator.  Indeed, as grows, if one projects out the relative frequencies nearest the Born ones containing a fixed large fraction---say 0.95---of the modulus squared of the state, there are more different frequency eigenvectors superposed as .  Of course, the numerical range of the frequencies also converges around the Born rule ones, roughly as .  It's a weak law of large numbers kind of thing---convergence in mean to the Born probabilities.  But it's not convergence to an eigenstate of the frequency operator.  This point, if I remember correctly, was first driven home to me by Ruediger Schack, at a time when I thought the convergence of most of the statevector modulus to a narrower and narrower range around the Born probabilities, was a pretty good argument that if you have to assign probabilities to outcomes in the Many Worlds interpretation, and you are willing to say that the probability assignment to a subspace should be uniformly continuous in the squared modulus of the state vector component in that subspace, then you should assign probabilities according to the Born rule.

I no longer care so much about this argument.  I now think the major issue for the Everett (Many Worlds) interpretation is whether one can reasonably use probabilistic notions at all, something that on my view this argument already presupposes one can do, as to neglect of a small-squared-modulus component of the wavefunction is effectively to declare that they have negligible probability, for the purposes at hand.  At dinner, Alan argued that even classically, one has to neglect the large number of outcome sequences ---exponentially larger than the number of sequences having frequencies near the probabilities---to argue that frequencies will "typically" be near the probabilities, even classically.  Neglecting a small-modulus portion of the state vector is thus no worse than what we do classically.  From a Bayesian---or more particularly, subjectivist/decision-theoretic point of view on how probability enters into these matters---the point is that this is justified for many purposes by the low probability, of these sequences, whereas someone who truly believes that the value of probability as a guide to describing and deciding about the world comes from properties of frequencies, doesn't really have anything to say to justify this neglect.  And there are things we can do to show that we cannot literally just treat all small probabilities as zero---for instance, we would not want to claim that, because the probability of each particular sequence of coin-toss outcomes is , we can ignore the possibility of getting a sequence with at least one tail, since each such sequence has negligible probability.  But Alan wasn't buying a Bayesian point of view here---he said he was interested in predicting the frequencies with which things occur, not in betting.  This is just a fundamental disagreement between us, and I tend to think that ultimately the frequentist point of view does not hang together sensibly, but this is not the point to go too far into it beyond what I said above about needing to presuppose probabilistic notions in order even to predict frequency.

But let's return to a frame of mind in which one does care about such arguments, and see what the consequences area of adopting the continuity assumption I made above, i.e. roughly "vanishingly low modulus of amplitude implies vanishingly low probability".  Does it really kill the argument to say that is not an eigenstate of any frequency operator?  What about  coarse-grained frequency operators, whose eigenspaces include subspaces spanned by the definite-frequency states with frequencies near the Born ones ?  We can gloss the continuity assumption I described above by calling it the "almost-an-eigenstate rule": states with large enough amplitude in an eigenspace count as having the associated eigenvalue.  This codifies Alan's "neglecting", and we may cash it out more delicately, for the subjectivist-inclined probabilist---in terms of a probabilistic assumption:  that the probability of having an eigenstate is uniformly continuous in the modulus of the state's component in the associated eigenspace.   This assumption is, at least, significantly weaker, at first glance, than assuming the Born rule straight away.  And then it would seem to allow one to conclude, that the probability of observing relative frequencies close to the Born ones, grows with large .  More to the point, perhaps, the probability of observing any other relative frequencies, within the same tolerance, becomes negligible.  At any , of course, there will always be frequencies that we can't rule out.  But it does look like only the Born rule is self-consistent in the sense that only for that rule will the amplitude of the states having frequencies within a shrinking interval of width proportional to around the proposed probabilities, approach with increasing .

I should probably think a bit more about things before posting this since there may be some elementary objection to the considerations I've just given, but as it's a blog, what the heck---I'll leave this hanging in the void of cyberspace for now, and risk being shown up by some comment, though this would appear unlikely if the past is any guide...

One parting point is that there are more comments on this issue in Matt Leifer's blog, under the neutral title "Anyone for Frequentist Fudge?",  which I came across while working on this post, and recomend  highly.  Matt objects to assiging "worlds with small amplitudes a small probability (which we do not do because that is what we're trying to derive".  I tend to agree, but strictly speaking it's only part of what we're trying to derive, so it's at least interesting that---if you buy the apparatus of for representing independent trials, which I guess is pretty standard (although Peter Byrne (see previous post) seemed to be claiming Everett may have introduced it)---you appear to be able to get from it, to a demonstration that only the Born probabilities satisfy the self-consistency property I described above.

Foundational Questions in the Azores I: Peter Byrne on Hugh Everett and Many Worlds

Posted on by

So far, there hasn't been much physics in Wine, Physics, and Song---nor much song, for that matter, though there's been plenty of wine, and some economics and politics.  I guess wine is easier and more relaxing to write about.  But it's time to redress that balance.

I arrived in Ponta Delgada, the main town of the island of São Miguel in the Portuguese archipelago of the Azores, courtesy of the Foundational Questions Institute, to attend and speak at their second annual conference.  We were treated to dinner and an after-dinner talk.  (The wines, especially a white called  something like Tierra de Lavas that was served before dinner, were tasty.)  The talk was by Peter Byrne, who is writing a biography of Hugh Everett III, the originator (unless you want to ascribe it to Schrödinger in his cat paper) of what he called the "relative state" interpretation of quantum mechanics, often called the "many worlds interpretation" (MWI).  I was particularly interested in this talk because a fascination with the problem of how to interpret quantum theory is a large part of what got me into physics.  In 1989--1990 I wrote a paper (unpublished), "The Many-Worlds Interpretation of Quantum Mechanics: Psychological versus Physical Bases for the Multiplicity of "Worlds", arguing that Everett's interpretation had often been misunderstood as involving a "physical" splitting of the universe into different branches, whereas Everett was actually fairly clear that the "branching" into parts of the universe involving different outcomes of a quantum experiment was associated with different subspaces of a single Hilbert space of the world, subspaces defined by which of the different macroscopic outcomes of the experiment an observer had experienced.  So I was very interested to hear from Peter Byrne that among the boxes of Everett's paper that he has been sorting and studying, were drafts of Everett's thesis in which there is much more extensive discussion of splitting minds than was available even in the long version of his thesis published by Princeton.  If I'm reporting Byrne correctly, one of these drafts compares the splitting minds to splitting amoebas, noting there is no fact of the matter as to which of the amoebas is the original one.  The whole thing, he says, had much more extensive discussion of splitting, which his advisor John Wheeler made him take out (partly, if I understood correctly, because of negative comments by Bohr, relayed by Stern who was on Everett's thesis committee).   It will be interesting to see the details of these drafts, and find out more about how Everett understood this "splitting".

My early paper was to some extent a "devil's advocate" exercise---I did not then, and do not now, believe in Everett's interpretation in the sense that a macroscopically entangled wavefunction, describing me having all kinds of different conscious experiences, is a real entity.  But I did believe, and still do, that pushing Everett's idea as far as possible is one good way of getting a better understanding of what is weird about quantum theory, and of the unexpected difficulties we've encountered in figuring out what quantum physics has to tell us about the world, and our place in it.

My reasons for not accepting many worlds are in part tied up with the fact that there don't seem to be probabilities of measurement outcomes on this interpretation, as there are indeed not definite classical outcomes.  More on this later---it is something that I've been thinking about for years, and before Byrne's talk, I had a long discussion about it with Alan Guth at dinner.   But one last thing:  it was therefore striking to hear from Byrne that one of a myriad of titles Everett considered for his dissertation was "Wave mechanics without probability".