Wine, Physics, and Song

To take up where I left off, I was discussing the Many Worlds interpretation of quantum mechanics with Alan Guth at dinner the first night of the FQXi conference in the Azores.  If I understood correctly, he seemed to think that the Many Worlds (in the sense of One Hilbert Space—Many Mutually Orthogonal Subspaces in which macroscopically distinct things appear to be happening) interpretation was useful, perhaps needed, to deal with quantum effects in cosmology.  I asked him whether he though the question of justifying the Born probability rule in the MWI was an important issue, and whether he had any opinions on it.  (The Born rule,  introduced by Max Born early in the history of quantum theory, in a famous footnote in a paper of his, it says, rougly speaking,  that the probability of finding a given outcome of a quantum measurement is given by the square of the modulus (”absolute value” of a complex number) of the complex component of the state vector in the subspace corresponding to that outcome.)  He advocated the Farhi-Gutmann version of an argument going back to James Hartle in 1965, and perhaps earlier to Finkelstein.  In his telling, the idea is that as long as one is willing to “neglect components of the wavefunction with vanishingly small modulus”, the fact that when one makes 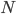repetitions of the same measurement on the same state 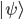of Hilbert space 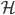(prepared again for each measurement) the state is represented by a tensor products 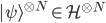implies that the state is (except for a negligible component) in a subspace in which frequencies are close to those given by the Born rule—approaching the Born frequencies ever more closely as 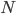gets larger.

Hopefully I’ve rendered what Guth had in mind reasonably well—we didn’t formalize things on a napkin or anything.  In some versions of this argument, one actually goes to an infinite tensor product Hilbert space, and the claim is made that the vector corresponding to an infinite number of independent preparations of 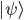—call it 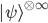if you like—just is an eigenstate of a “relative frequency operator” on this infinite tensor product Hilbert space, with eigenvalue equal to the Born probabilities.  I believe that’s the claim of the Farhi and Gutmann paper — but Caves and Schack claim it’s incorrect.  Then—by the “eigenvalue-eigenstate link”, which is a “minimalist” interpretation of the state vector’s relation to actual observational outcomes, saying that if a state actually has a definite eigenvalue for some observable, than the outcome corresponding to that eigenvalue is actual (perhaps this can be thought of as assigning probabilities 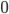and to outcome subspaces in which the state has zero component, or in which the state is contained, respectively)—one concludes that the Born rule probabilities are the only ones that give the correct relative frequencies, in the infinite limit.

Whether or not the claim about the infinite state being an eigenstate of relative frequency is correct, I’m suspicious of arguments that require an actualized infinity—I try to understand them by understanding the actual limit as summarizing—albeit with some quantitative details of rates of convergence suppressed—how things “can be made to look in large finite cases”—i.e., the 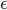’s and 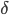’s rule my understanding.  So—without having looked at the Farhi and Gutmann paper recently, however—let’s think about this; it’s something I’ve thought about before.  Basically, it seems to me incorrect to claim that the state approaches an eigenstate of a sharp relative frequency operator—although the expectation value of its relative frequency list approaches the Born rule probabilities, as 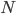grows it remains in a superposition of eigenstates of the 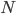-th relative frequency operator.  Indeed, as 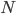grows, if one projects out the relative frequencies nearest the Born ones containing a fixed large fraction—say 0.95—of the modulus squared of the state, there are more different frequency eigenvectors superposed as 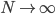.  Of course, the numerical range of the frequencies also converges around the Born rule ones, roughly as 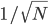.  It’s a weak law of large numbers kind of thing—convergence in mean to the Born probabilities.  But it’s not convergence to an eigenstate of the frequency operator.  This point, if I remember correctly, was first driven home to me by Ruediger Schack, at a time when I thought the convergence of most of the statevector modulus to a narrower and narrower range around the Born probabilities, was a pretty good argument that if you have to assign probabilities to outcomes in the Many Worlds interpretation, and you are willing to say that the probability assignment to a subspace should be uniformly continuous in the squared modulus of the state vector component in that subspace, then you should assign probabilities according to the Born rule.

I no longer care so much about this argument.  I now think the major issue for the Everett (Many Worlds) interpretation is whether one can reasonably use probabilistic notions at all, something that on my view this argument already presupposes one can do, as to neglect of a small-squared-modulus component of the wavefunction is effectively to declare that they have negligible probability, for the purposes at hand.  At dinner, Alan argued that even classically, one has to neglect the large number of outcome sequences —exponentially larger than the number of sequences having frequencies near the probabilities—to argue that frequencies will “typically” be near the probabilities, even classically.  Neglecting a small-modulus portion of the state vector is thus no worse than what we do classically.  From a Bayesian—or more particularly, subjectivist/decision-theoretic point of view on how probability enters into these matters—the point is that this is justified for many purposes by the low probability, of these sequences, whereas someone who truly believes that the value of probability as a guide to describing and deciding about the world comes from properties of frequencies, doesn’t really have anything to say to justify this neglect.  And there are things we can do to show that we cannot literally just treat all small probabilities as zero—for instance, we would not want to claim that, because the probability of each particular sequence of 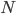coin-toss outcomes is 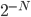, we can ignore the possibility of getting a sequence with at least one tail, since each such sequence has negligible probability.  But Alan wasn’t buying a Bayesian point of view here—he said he was interested in predicting the frequencies with which things occur, not in betting.  This is just a fundamental disagreement between us, and I tend to think that ultimately the frequentist point of view does not hang together sensibly, but this is not the point to go too far into it beyond what I said above about needing to presuppose probabilistic notions in order even to predict frequency.

But let’s return to a frame of mind in which one does care about such arguments, and see what the consequences area of adopting the continuity assumption I made above, i.e. roughly “vanishingly low modulus of amplitude implies vanishingly low probability”.  Does it really kill the argument to say that 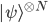is not an eigenstate of any frequency operator?  What about  coarse-grained frequency operators, whose eigenspaces include subspaces spanned by the definite-frequency states with frequencies near the Born ones ?  We can gloss the continuity assumption I described above by calling it the “almost-an-eigenstate rule”: states with large enough amplitude in an eigenspace count as having the associated eigenvalue.  This codifies Alan’s “neglecting”, and we may cash it out more delicately, for the subjectivist-inclined probabilist—in terms of a probabilistic assumption:  that the probability of having an eigenstate is uniformly continuous in the modulus of the state’s component in the associated eigenspace.   This assumption is, at least, significantly weaker, at first glance, than assuming the Born rule straight away.  And then it would seem to allow one to conclude, that the probability of observing relative frequencies close to the Born ones, grows with large 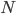.  More to the point, perhaps, the probability of observing any other relative frequencies, within the same tolerance, becomes negligible.  At any 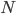, of course, there will always be frequencies that we can’t rule out.  But it does look like only the Born rule is self-consistent in the sense that only for that rule will the amplitude of the states having frequencies within a shrinking interval of width proportional to 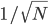around the proposed probabilities, approach with increasing .

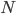I should probably think a bit more about things before posting this since there may be some elementary objection to the considerations I’ve just given, but as it’s a blog, what the heck—I’ll leave this hanging in the void of cyberspace for now, and risk being shown up by some comment, though this would appear unlikely if the past is any guide…

One parting point is that there are more comments on this issue in Matt Leifer’s blog, under the neutral title “Anyone for Frequentist Fudge?“,  which I came across while working on this post, and recomend  highly.  Matt objects to assiging “worlds with small amplitudes a small probability (which we do not do because that is what we’re trying to derive”.  I tend to agree, but strictly speaking it’s only part of what we’re trying to derive, so it’s at least interesting that—if you buy the apparatus of 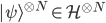for representing independent trials, which I guess is pretty standard (although Peter Byrne (see previous post) seemed to be claiming Everett may have introduced it)—you appear to be able to get from it, to a demonstration that only the Born probabilities satisfy the self-consistency property I described above.

This entry was posted on Wednesday, September 2nd, 2009 at 12:10 pm and is filed under Foundations of Quantum Theory, Physics, Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.