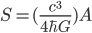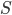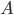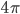Tag Archives: entropy

Answer to question about Bekenstein BH entropy derivation

Posted on by

I had a look at Jacob Bekenstein's 1973 Physical Review D paper "Black holes and entropy" for the answer to my question about Susskind's presentation of the Bekenstein derivation of the formula stating that black hole entropy is proportional to horizon area.  An argument similar to the one in Susskind's talk appears in Section IV, except that massive particles are considered, rather than photons, and they can be assumed to be scalar so that the issue I raised, of entropy associated with polarization, is moot.  Bekenstein says:

we can be sure that the absolute minimum of information lost [as a particle falls into a black hole] is that contained in the answer to the question "does the particle exist or not?"  To start with, the answer [to this question] is known to be yes.  But after the particle falls in, one has no information whatever about the answer.  This is because from the point of view of this paper, one knows nothing about the physical conditions inside the black hole, and thus one cannot assess the likelihood of the particle continuing to exist or being destroyed.  One must, therefore, admit to the loss of one bit of information [...] at the very least."

Presumably for the particle to be destroyed, at least in a field-theoretic description, it must annihilate with some stuff that is already inside the black hole (or from the outside point of view, plastered against the horizon). This annihilation could, I guess, create some other particle. In fact it probably must, in order to conserve mass-energy.  My worry in the previous post about the entropy being due to the presence/absence of the particle inside the hole was that this would seem to need to be due to uncertainty about whether the particle fell into the hole in the first place, which did not seem to be part of the story Susskind was telling, and the associated worry that this would make the black hole mass uncertain, which also didn't seem to be a feature of the intended story although I wasn't sure. But the correct story seems to be that the particle definitely goes into the hole, and the uncertainty is about whether it subsequently annihilates with something else inside, in a process obeying all relevant conservation laws, rendering both of my worries inapplicable. I'd still like to see if Bekenstein wrote a version using photons, as Susskind's presentation does. And when I feel quite comfortable, I'll probably post a fairly full description of one (or more) versions of the argument. Prior to the Phys Rev D paper there was a 1972 Letter to Nuovo Cimento, which I plan to have a look at; perhaps it deals with photons. If you want to read Bekenstein's papers too, I suggest you have a look at his webpage.

Question about Susskind's presentation of Bekenstein's black hole entropy derivation

Posted on by

I'm partway through viewing Leonard Susskind's excellent not-too-technical talk "Inside Black Holes" given at the Kavli Institute for Theoretical Physics at UC Santa Barbara on August 25.  Thanks to John Preskill,  @preskill, for recommending it.

I've decided to try using my blog as a discussion space about this talk, and ultimately perhaps about the "Harlow-Hayden conjecture" about how to avoid accepting the recent claim that black holes must have an information-destroying "firewall" near the horizon.  (I hope I've got that right.)  I'm using  Susskind's paper "Black hole complementarity and the Harlow-Hayden conjecture"  as my first source on the latter question.  It also seems to be a relatively nontechnical presentation (though much more technical than the talk so far)... that should be particularly accessible to quantum information theorists, although it seems to me he also does a good job of explaining the quantum information-theoretic concepts he uses to those not familiar with them.

But first things first.  I'm going to unembarassedly ask elementary questions about the talk and the paper until I understand.  First off, I've got a question about Susskind's "high-school level" presentation, in minutes 18-28 of the video, of Jacob Bekenstein's 1973 argument that in our quantum-mechanical world the entropy of a black hole is proportional to its area (i.e. the area of the horizon, the closed surface inside which nothing, not even light, can escape).   The formula, as given by Susskind, is

,

where is the entropy (in bits) of the black hole, and the area of its horizon.  (The constant here may have been tweaked by a small amounts, like or its inverse, to reflect considerations that Susskind alluded to but didn't describe, more subtle than those involved in Bekenstein's argument.)

The argument, as presented by Susskind, involves creating the black hole out of photons whose wavelength is roughly the Schwarzschild radius of the black hole.  More precisely, it is built up in steps; each step in creating a black hole of a given mass and radius involves sending in another photon of wavelength roughly the current Schwarzschild radius.  The wavelength needs to be that big so that there is no information going into the hole (equivalently, from the point of view outside the hole, getting "plastered" (Susskind's nice choice of word) against the horizon) about where the photon went in.  Presumably there is some argument about why the wavelength shouldn't be much bigger, either...perhaps so that it is sure to go into the hole, rather than missing.  That raises the question of just what state of the photon field should be impinging on the hole...presumably we want some wavepacket whose spatial width is about the size of the hole, so we'll have a spread of wavelengths centered around some multiple (roughly unity) of the Schwarzschild radius.  Before there is any hole, I guess I also have some issues about momentum conservation... maybe one starts by sending in a spherical shell of radiation impinging on where we want the hole to be, so as to have zero net momentum.  But these aren't my main questions, though of course it could turn out to be necessary to answer them in order to answer my main question.  My main question is:  Susskind says that each such photon carries one bit of information: the information is "whether it's there or not".  This doesn't make sense to me, as if one is uncertain about how many photons went into creating the hole, it seems to me one should have a corresponding uncertainty about its mass, radius, etc...  Moreover, the photons that go in still seem to have a degree of freedom capable of storing a bit of information:  their polarization.  So maybe this is the source of the one bit per photon?  Of course, this would carry angular momentum into the hole/onto the horizon, so I guess uncertainty about this could generate uncertainty about whether or not we have a Schwarzschild or a Kerr (rotating) black hole, i.e. just what the angular momentum of the hole is.

Now, maybe the solution is just that given their wavelength of the same order of the hole, there is uncertainty about whether or not the photons actually get into the hole, and so the entropy of the black hole really is due to uncertainty about its total mass, and the mass M in the Bekenstein formula is just the expected value of mass?

I realize I could probably figure all this out by grabbing some papers, e.g. Bekenstein's original, or perhaps even by checking wikipedia, but I think there's some value in thinking out loud, and in having an actual interchange with people to clear up my confusion... one ends up understanding the concepts better, and remembering the solution.  So, if any physicists knowledgeable about black holes (or able and willing to intelligently speculate about them...) are reading this, straighten me out if you can, or at least let's discuss it and figure it out...