Interesting-looking bit of political economy research.  They propose that sectors employing lower-earning workers more intensively are receive relatively more trade protection, based on research in the US and China, and apparently attempt to differentiate between the contributions of envy and altruism to this effect.  Also, presumably, compare it to theories where amount of protection depends primarily on the resources available to an industry to help secure it.  NBER charges five bucks (OK, that beats Springer journals hands-down, but still) to download, so unless PI gets a subscription, looks like I'm not reading it.  What is with charging money for working papers!?  Can't we get these economists on the arXiv???

Proving that Proving is Hard.  Computer scientist Dick Lipton gives a beautiful introduction to work by Fischer and Rabin on the computational complexity of the formal first-order theory of the real numbers.  As Lipton explains, Alfred Tarski showed that this theory is complete---that every well-formed statement in the language of the theory can either be proved, or be disproved, from the axioms of the theory. Fischer and Rabin investigated how hard it can be to prove statements in the theory.   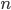According to Lipton, they showed that it's (worst-case) exponentially hard:  there is a positive constant such that there are true sentences of the theory, of length shorter than , whose shortest proof has length at least 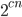.  (I'd guess what's meant is that they show this holds for all large enough 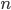, or at least for an infinite set of .)

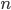Quantifier elimination---the method of deciding statements in the theory of the reals, used by Tarski in his decidability proof---has, at least theoretically, applications in optimization, which I hope to delve into in a future post.

A nice, probably not-too-easy (for me) and not-too-hard problem in group theory from my colleague Alberto Montina: is 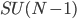a subgroup of 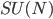of maximal dimension (as a manifold) and are there any others.

Paul Halmos, How to Write Mathematics.