Pablo Arrighi of the University of Grenoble spoke on his result, with collaborators Vincent Nesme and Reinhard Werner (both now at the Leibniz University Hannover), that  Unitarity plus Causality implies Locality, at the PiQuDos seminar today at Perimeter.  I heard him speak on this result over a year ago at Foundational Structures for Quantum Information and Computation at Obergurgl, Austria;  I thought it was one of the standout talks of the workshop, and his talk today, which also covered more recent work along the same lines, reminded me how interesting I'd found his result when I first heard it.

Arrighi, Nesme, and Werner consider a quantum system associated with a graph having a countably infinite number of vertices, and an arbitrary edge structure.  At each vertex is a quantum system, finite or infinite dimensional, represented by a Hilbert space.  The edge structure is supposed to represent some notion of two systems being "nearby", so that it's physically reasonable for them to influence each other during one step of time evolution.  Roughly speaking, this is their notion of "causality" of a time evolution: that only such nearby systems have any influence on each other.  They define a Hilbert space associated with this infinite set of quantum systems.  It's not quite the tensor product of this infinite set of Hilbert spaces (which would not necessarily be a Hilbert space), but rather the span of all "finitely supported configurations", i.e. product states having a special state 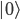on all but a finite number of systems.  (You can do things 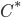-algebraically and do better, Pablo said, but this should be good enough.)  Their main result states, roughly speaking, that if a unitary evolution satisfies "causality", it can be represented as a circuit of quantum operators each acting on a neighborhood (a vertex and its neighbors) in the graph; the circuit has depth no greater than the square of the degree of the graph, plus 2.  (The degree of the graph is the largest number of edges emanating from a vertex.  For example, in lattices that repeat a hypercube of some dimension as their basic structure, the degree is twice the dimension).  In other words, there is a representation via "local"---although multi-way---interactions, happening in parallel on disjoint neighborhoods.  It may be necessary to take several successive rounds of interactions, happening on different sets of neigborhoods, but it's never necessary to take more than the degree squared plus two rounds.  So in a "spatial" hypercubic lattice in N dimensions, you never need more than 4N^2+2 rounds of interactions of interactions with neighbors.  (True, these are 2N+1-body interactions.)

I still haven't finished saying what the result is, because I didn't yet say (except roughly at the beginning) what the assumption of causality is.  It's that the state of the quantum system at a vertex after the overall unitary evolution U on the entire (infinite!) graph, depends only on the state of its neighbors before the evolution.  By state, he means reduced density matrix, after the other systems are traced out.  (Equivalently, in the Heisenberg picture we could say that an operator "supported only at site x", i.e. of the form "A at site x tensor the identity everywhere else", has, when evolved with 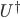, support only at the neigborhood of x, i.e., is of the form "Something on the tensor product of x's neighborhood, tensored with the identity everyplace else".)

Now, given that causality is defined by the influence of a state at a node in the graph propagating only to nearest neighbors (and the node itself) during the unitary evolution, it's perhaps not so surprising that it has a representation in terms of interactions among neighbors.  The important thing to remember, though, is that the causality condition concerns all the overlapping neighborhoods in the graph simultaneously, while the circuit-local representation involves only nonoverlapping neighborhoods, interacting in parallel, in each layer of the circuit, and bounds the number of layers as described above.

Actually, what I've described is a corollary to the main theorem, since this corollary has more immediate intuitive import.  I'll leave you to follow the link to the paper at the beginning of this post, if you want to see the details of the theorem as well.  Also, I've talked as if an edge between two nodes means that either node can influence the other during the evolution; actually, the authors allow for directed graphs, so that (x,y) maybe be an edge in the graph without (y,x) also being one;  the notions of causality and locality are then adjusted to refer to the graph and its transpose (i.e. the one specified by transposing its adjacency matrix) appropriately.  Here, a directed edge (x,y) in the graph means site x can influence site y in one step of unitary evolution;  (y,x) means y can influence x, and it's possible in their framework to allow influence in one direction but not the other, if desired.

One more thing, though: for those who think that this is too obvious, according to Pablo the analogous theorem probably doesn't hold if unitaries are replaced by completely positive maps.  He also thinks there is not a direct analogue even for classical stochastic evolution.  The development of an appealing strengthening of Causality that would allow a similar representation theorem for completely positive maps is something he's actively working on.

The talk also covered some related work that's more recent, such as cool results about the notion of "intriniscally universal" quantum cellular automata on certain kinds of graphs.  These things can simulate the action of any other cellular automaton by means of a short encoding, which takes the state of each cell in the simulated automaton to an encoded state on a block of adjacent cells in the graph of the universal automaton;  several steps---say, 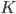steps---of the universal automaton then simulate the action of the simulated automaton, on the encoded state.  After 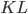steps of the universal automaton, one can apply the inverse of the encoding map, to obtain the state that would have been obtained under 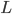steps of the simulated automaton.   A paper (with Jonathan Grattage)   is here.

The talk should soon be available at PIRSA.