Next time you're at a party and someone asks "hey, did you hear that Britney Spears was seen with the lead actor from Desperate Housewives at an L.A. disco last week?", try replying "No, but did you hear that Rahul Jain, Zhengfeng Ji, Sarvagya Uphadyay, and John Watrous showed that QIP=PSPACE in July?  This is likely to be a foolproof way of ensuring you don't get invited to any parties hosted by your interlocutor, which is likely to be a good thing.  If, however, your conversation partner is thinking fast enough to  reply, "No, so give me the skinny on it," you're going to want to be prepared.  Luckily it's not all that hard.  This is the first in a series of posts that will enable you to answer such a comeback in detail, captivating entire the party for at least a short while, and clearing your social schedule for months to come, as well as leaving you free in the moderately near-term to enjoy whatever remains of the Sutter Home Pink Zinfandel at the drinks table.  John Watrous gave an excellent colloquium at the IQC (Institute for Quantum Computing) yesterday, on the above-referenced work showing the the complexity classes QIP and PSPACE are identical. I originally imagined writing a fairly technical post aimed at colleagues; they will probably want to skip to number II or maybe even III; this post sets the stage for defining the complexity classes QIP and PSPACE, by reviewing the notion of complexity classes.

Complexity classes are, roughly speaking, sets (although I imagine the term "class" is used instead of "set" advisedly, for the set-theory-minded among you---perhaps I will come back to this) of computational problems.  Normally, they are taken to be classes of decision problems: problems of the form:  given an input from a set of possible inputs (the specification of this set is part of the specification of a particular computational problem), decide whether it has, or does not have, a certain property.  To say that a computer program solves such a problem is to say that it outputs "0" if the input doesn't have the property, and "1" if it does.  Normally, the set of possible inputs to a computational problem is taken to be countably infinite (like, for instance, the integers, or the set of finite-length strings of 0's or 1's ("binary strings"), or the set of ASCII text strings...).  So, an example of a problem would be "take a finite string of 0s and 1s; is the number of 1s odd?"  This problem is called PARITY, since evenness or oddness is a property known as the "parity" of a number.  Another example, often called OR, also involves binary strings as inputs; it asks, "is there a 1 in the string"?  Determining whether an integer is prime or not is another example; where the inputs are now integers instead of binary strings.  (But they can be coded, and often are coded, as binary strings---that is, they are written in their base-2 expansion.)  A problem that takes pairs of integers, instead of single integers, as inputs is to determine whether one integer divides another.  There are also more complicated problems, in which the output is not "0" or "1", but is drawn from a larger set of possibilities, but we won't discuss them much here.  An example would be: given an integer, tell us whether or not it is prime and if it isn't, exhibit a nontrivial factorization of it.

Not just any class of decision problems is a complexity class, although I haven't seen (nor do I expect to see) a formal definition of "complexity class", or even much in the way of necessary conditions for being a complexity class.  A complexity class is supposed to reflect something about how hard it is to solve a decision problem, and is often described as "the set of all problems that can be solved by computations of *this sort*", where "this sort" describes some model of how one might do computations.  The model is often quite zany compared to how we actually compute things, but it's rigorously specified.

Now, a computational decision problem, as we've defined it, in most cases clearly can't be "solved" once and for all by a computer.  It involves a countably infinite set of possible inputs, and so the "full solution" would involve listing, for each of these inputs, whether the answer is "0" or "1".  This answer would take an infinite amount of space (and presumably an infinite amount of time, given a lower bound on the amount of time it takes to write a character) just to write down.  So if we want to relate problems like this to reasonable notions of computation, we need to discuss programs that give the right answer for whatever input is presented.  To say things about how hard the problem is is not to say how hard it is to write down all the answers, but rather we need a notion of how hard it is to do the computation on an input.  What's often done is to study how the resources required---the number of computational steps, and the amount of computer memory needed---scale with the size of the input.  This means, of course, that we need not just a countable set of inputs, but one equipped with a notion of size.  In the case of binary strings, the length of the string is what's used.  This works for numbers, too---we just use the number of bits in the binary expansion.  (Up to a constant factor, this is the same as the number of digits in its decimal expansion.)  This is why you may need to choose things like "128-bit RSA key" versus "256-bit RSA key" when doing secure internet transactions, for example:  the security of these transactions is based on the idea that it's hard to factor integers, and what "hard" means here is roughly that the amount of computational resources needed to factor grows faster than any polynomial, with the number N of bits in the binary expansion of the number.  If I remember correctly, the worst-case resources for factoring an N-bit number using the best currently known algorithms scale as around 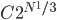, i.e. they are (up to a proportionality constant C) exponential in the cube root of the number of bits.  More needs to be said, of course---not every N-bit number will take this long to factor, but for large enough N, some numbers will take this long.  For cryptographic security, it's actually important to use a procedure for choosing key that is overwhelmingly likely to pick such hard instances---multiplying together large enough primes is, I guess, thought to work.  This is, of course, a side issue:  the main point is that the definitions of complexity classes often contain reference to how the resources used by a program that solves a decision in problem in the class, in a particular model of computation, scale with the size of the input.  The very important complexity class P, for polynomial time, is roughly the class of decision problems for which there's a polynomial Q (the polynomial may depend on the problem) that gives an upper bound to the time that it takes to solve the problem in a standard computational model closely related to actual computers, namely the Turing machine model (or any model polynomially equivalent to this, such as the 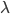-calculus introduced by Alonzo Church at around the same time Turing introduced the Turing machine).  That is, if 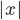is the length of input 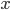, the time it takes a Turing machine to solve the problem on input 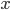is no greater than .

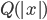The notion of polynomial time computation is important in the definition of many other complexity classes, and it's also the complexity class that's perhaps the most reasonable candidate for a class of "efficiently solvable" decision problems.  In actual practice, of course, we often solve smallish instances---or expend huge amounts of resources to solve moderate-sized instances---of problems from harder complexity classes;  and occasionally, we have polynomial algorithms for problems for which we'd like to solve large instances, but can't because the degree of the polynomial is too high.  If you hang out with cell-phone security folks, for instance, you'll find that encoding and decoding of messages that is linear in key length is considered a huge advantage compared to quadratic in the key length; forget about higher degree.  Here the small size of cell-phone processors is important.  But degree of a polynomial---and even, sometimes, the constant out front---can be important for big machines, too.  The ellipsoids methods for linear and semidefinite programming, although polynomial, has seen little practical use; interior-point methods, also polynomial, revolutionized the field as they perform much better in practice.  (I'm ashamed to say I don't know offhand if it's the constant or the degree that's mostly responsible for this.)  Actually, for LP the simplex method, which is worst-case exponential, is still in wide use because it performs just fine on most instances---the hard ones appear to be rare and bizarre.  But despite these caveats, P is an important complexity class, with a definite relevance to the line between what it's practical to compute and what it's not.

In the next instalment, I'll cover the classes IP, QIP, and PSPACE---classes that, it's pretty clear, go far beyond what it's practical to compute, but which are fun to think about nonetheless.  (I presume they have more scientific relevance than just being fun; perhaps we can be enlightened about that in the comments.)